广东省潮州市潮安区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 下列式子没有意义的是( )A、 B、 C、 D、2. 在下列长度的各组线段中,能组成直角三角形的是( )A、5,6,7 B、1,4,8 C、5,12,13 D、5,11,123. 下列计算正确的是( )A、 B、 C、 D、4. 射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为 , , , ,则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )A、y= B、y= C、y= D、y=6. 如图,在菱形ABCD中, ,则 ( )
 A、30° B、45° C、60° D、75°7. 某中学对该校九年级45名女学生进行了一次立定跳远测试,成绩如表:
A、30° B、45° C、60° D、75°7. 某中学对该校九年级45名女学生进行了一次立定跳远测试,成绩如表:跳远成绩
160
170
180
190
200
210
人数
3
9
6
9
15
3
这些立定跳远成绩的中位数和众数分别是( )
A、9,9 B、15,9 C、190,200 D、185,2008. 如图所示,以 的三边为边向外作正方形,其面积分别为 ,且 , ,则 ( ) A、4 B、8 C、12 D、329. 如图,在▱ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是( )
A、4 B、8 C、12 D、329. 如图,在▱ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是( )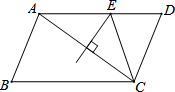 A、8 B、6 C、9 D、1010. 能表示一次函数y=mx+n与正比例函数y=mnx(m , n是常数且m≠0)的图象的是( )A、
A、8 B、6 C、9 D、1010. 能表示一次函数y=mx+n与正比例函数y=mnx(m , n是常数且m≠0)的图象的是( )A、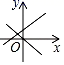 B、
B、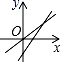 C、
C、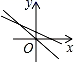 D、
D、
二、填空题
-
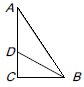
11. 如图 ,在△ ABC 中,∠C=90°,∠ABC 的平分线 BD 交 AC 于点 D.若 BD=10cm,BC=8cm,则点 D 到直线 AB 的距离= .
 12. 将一次函数y=3x﹣1的图象沿y轴向上平移3个单位后,得到的图象对应的函数关系式为 .13. 如图,在矩形 中, 为 的中点,且 ,则 的长为 .
12. 将一次函数y=3x﹣1的图象沿y轴向上平移3个单位后,得到的图象对应的函数关系式为 .13. 如图,在矩形 中, 为 的中点,且 ,则 的长为 . 14. 一个弹簧不挂重物时长10cm,挂上重物后伸长的长度与所挂重物的质量成正比,如果挂上1kg的物体后,弹簧伸长3cm,则弹簧总长y(单位:cm)关于所挂重物x(单位:kg)的函数关系式为(不需要写出自变量取值范围)15. 已知数据 的平均数是2,方差是3,则一组新数据 的平均数是 , 方差是 .16. 已知函数 与函数 的图象交于点P,则不等式 的解集是 .
14. 一个弹簧不挂重物时长10cm,挂上重物后伸长的长度与所挂重物的质量成正比,如果挂上1kg的物体后,弹簧伸长3cm,则弹簧总长y(单位:cm)关于所挂重物x(单位:kg)的函数关系式为(不需要写出自变量取值范围)15. 已知数据 的平均数是2,方差是3,则一组新数据 的平均数是 , 方差是 .16. 已知函数 与函数 的图象交于点P,则不等式 的解集是 .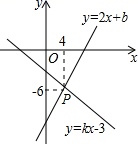 17. 如图,点 分别是 的中点,下列结论:① ;②当 , 平分 ;③当 时,四边形 是矩形;其中正确的结论序号是 .
17. 如图,点 分别是 的中点,下列结论:① ;②当 , 平分 ;③当 时,四边形 是矩形;其中正确的结论序号是 .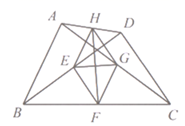
三、解答题
-
18. 计算:19. 已知在 中, ,求作:矩形ABCD(用尺规作图法,保留作图痕迹,不要求写作法)
 20. 一次函数 的图像经过点 和点 ,请判断点 是否在此直线上并说明理由.21. 王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
20. 一次函数 的图像经过点 和点 ,请判断点 是否在此直线上并说明理由.21. 王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示. (1)、分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;(2)、试通过计算说明,哪个山上的杨梅产量较稳定?22. 如图,在正方形 中,动点 在 上, ,垂足为 , .
(1)、分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;(2)、试通过计算说明,哪个山上的杨梅产量较稳定?22. 如图,在正方形 中,动点 在 上, ,垂足为 , . (1)、求证: ;(2)、当点 运动到 的中点时(其他条件都保持不变),四边形 是什么特殊四边形?请说明,理由.23. A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A校调运一台电脑到C校和D校的运费分别为40元和80元;从B校调运一台电脑到C校和D校的运费分别为30元和50元.
(1)、求证: ;(2)、当点 运动到 的中点时(其他条件都保持不变),四边形 是什么特殊四边形?请说明,理由.23. A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A校调运一台电脑到C校和D校的运费分别为40元和80元;从B校调运一台电脑到C校和D校的运费分别为30元和50元. (1)、设A校运往C校的电脑为x台,求总运费y(元)关于x的函数关系式;(2)、求出总运费最低的调运方案,最低运费是多少?24. 如图,已知直线 与 轴交于点A,与 轴交于点C,过点C的直线 与 轴交于点B.
(1)、设A校运往C校的电脑为x台,求总运费y(元)关于x的函数关系式;(2)、求出总运费最低的调运方案,最低运费是多少?24. 如图,已知直线 与 轴交于点A,与 轴交于点C,过点C的直线 与 轴交于点B.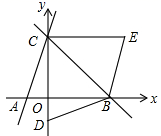 (1)、b的值为;(2)、若点D的坐标为 ,将 沿直线BC对折后,点D落到第一象限的点E处,求证:四边形ABEC是平行四边形.(3)、点P在线段BC上,且四边形PADB是平行四边形,求出点P的坐标.25. 如图,已知函数 的图像与 轴交于点A,一次函数 的图像经过点 ,与 轴以及 的图像分别交于点 ,且点D的坐标为 .
(1)、b的值为;(2)、若点D的坐标为 ,将 沿直线BC对折后,点D落到第一象限的点E处,求证:四边形ABEC是平行四边形.(3)、点P在线段BC上,且四边形PADB是平行四边形,求出点P的坐标.25. 如图,已知函数 的图像与 轴交于点A,一次函数 的图像经过点 ,与 轴以及 的图像分别交于点 ,且点D的坐标为 .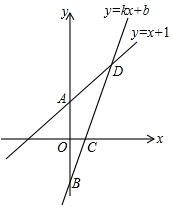 (1)、则 , , ;(2)、求四边形AOCD的面积;(3)、在 轴上是否存在点P,使得以点 为顶点的三角形时直角三角形?若存在求出点P的坐标;若不存在,请说明理由.
(1)、则 , , ;(2)、求四边形AOCD的面积;(3)、在 轴上是否存在点P,使得以点 为顶点的三角形时直角三角形?若存在求出点P的坐标;若不存在,请说明理由.