重庆市北碚区2020年数学中考模拟试卷（6月）

试卷更新日期：2020-09-14 类型：中考模拟

进入出卷网下载

一、单选题。

1. $\sqrt{64}$ 的立方根是（　　）

A、±2 B、±4 C、4 D、2

查看试题解析
2. 已知 $| a | = 3$ ， $| b | = 4$ ，且 $a b < 0$ ，则 $a-b$ 的值为（）

A、1或7 B、1或-7 C、±1 D、±7

查看试题解析
3. 已知 $x - \frac{1}{x} = 1$ ，则 $x^{2} + \frac{1}{x^{2}}$ 等于（）

A、3 B、2 C、1 D、0

查看试题解析
4. 下列算式：① $\sqrt{9} = \pm 3$ ；② ${(- \frac{1}{3})}^{-2} = 9$ ；③ $2^{6} \div 2^{3} = 4$ ；④ ${(\sqrt{-2020})}^{2} = 2020$ ；⑤ $a + a = a^{2}$ .运算结果正确的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
5. 已知， $x + y = - 5$ ， $x y = 3$ 则 $x \sqrt{\frac{y}{x}} + y \sqrt{\frac{x}{y}}$ 的结果是（）

A、 $2 \sqrt{3}$ B、 $- 2 \sqrt{3}$ C、 $3 \sqrt{2}$ D、 $- 3 \sqrt{2}$

查看试题解析
6. 如图，在平面直角坐标系中，∠AOB＝90°，∠OAB＝30°，反比例函数y₁＝ $\frac{m}{x}$ 的图象经过点A，反比例函数y₂＝ $\frac{n}{x}$ 的图象经过点B，则下列关于m，n的关系正确的是（）

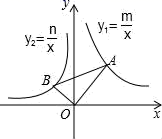A、m＝ $\frac{\sqrt{3}}{3}$ n B、m＝﹣ $\sqrt{3}$ n C、m＝﹣ $\frac{\sqrt{3}}{3}$ n D、m＝﹣3n

查看试题解析
7. 已知a、b、c为△ABC的三边，且满足a²c²﹣b²c²＝a⁴﹣b⁴ ，则△ABC是（）

A、直角三角形 B、等腰三角形 C、等腰三角形或直角三角形 D、等腰直角三角形

查看试题解析
8. 若不等式组 ${\begin{array}{l} 5 x + 2 \leq 3 x - 5 \\ - x + 5 < a \end{array}$ 无解，则a的取值范围是 $($ $)$

A、 $a \leq \frac{17}{2}$ B、 $a \leq 12$ C、 $a < \frac{17}{2}$ D、 $a < 12$

查看试题解析
9. 如图，平行四边形ABCD的对角线AC与BD相交于点O ， AE⊥BC于E ， AB＝ $\sqrt{3}$ ，AC＝2，BD＝4，则AE的长为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{3}{2}$ C、 $\frac{\sqrt{21}}{7}$ D、 $\frac{2 \sqrt{21}}{7}$

查看试题解析
10.
如图，已知直线l： $y = \frac{\sqrt{3}}{3} x$ ，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A₁；过点A₁作y轴的垂线交直线l于点B₁ ，过点B₁作直线l的垂线交y轴于点A₂；…；按此作法继续下去，则点A₄的坐标为（）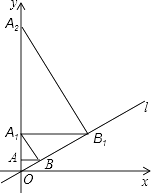

A、（0，128） B、（0，256） C、（0，512） D、（0，1024）

查看试题解析
11. 美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给人一种美感.如图，某女士身高165cm，下半身长x与身高l的比值是0.60，为尽可能达到美的效果，她应穿的高跟鞋的高度大约为（）

A、4cm B、6cm C、8cm D、10cm

查看试题解析
12. 若关于y的不等式组 ${\begin{array}{l} \frac{y - 1}{2} \geq 2 k \\ y-k \leq 4 k + 6 \end{array}$ 有解，且关于x的分式方程 $\frac{k x}{x - 2} = 2 - \frac{3 x + 2}{x - 2}$ 有非负整数解，则符合条件的所有整数k的和为（）

A、-5 B、-9 C、-10 D、-16

查看试题解析

二、填空题。

13. $\sqrt{16}$ 的算术平方根是， $\sqrt{5}$ ﹣2的相反数是　， $\sqrt[3]{- 8}$ 的绝对值是．

查看试题解析
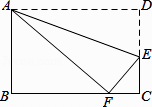
14. 已知xy=3，那么 $x \sqrt{\frac{y}{x}} + y \sqrt{\frac{x}{y}}$ 的值为 .

查看试题解析
15. 如图，在矩形ABCD中，AB=3，AD=5，点E在DC上，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，那么cos∠EFC的值是．

查看试题解析
16. 如图，二次函数y＝ax²+bx+c(a≠0)的图象与x轴交于A、B两点，与y轴交于点C，对称轴是直线x＝﹣1，点B的坐标为(1，0).下面的四个结论：①AB＝4；②b²﹣4ac＞0；③ab＜0；④a﹣b+c＜0，其中正确的结论是(填写序号).

查看试题解析
17.
在一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器的体积时，气体的密度也会随之改变，密度ρ（单位：kg/m³）与体积v（单位：m³）满足函数关系式ρ= $\frac{k}{v}$ （k为常数，k≠0）其图象如图所示，则k的值为．

查看试题解析
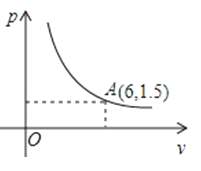18. 武汉某超市在疫情前用3000元购进某种干果销售，发生疫情后，为了保障附近居民的生活需求，又调拨9000元购进该种干果.受疫情影响，交通等成本上涨，第二次的进价比第一次进价提高了20%，但是第二次购进干果的数量是第一次的2倍还多300千克，如果超市先按每千克9元的价格出售，当大部分干果售出后，最后的600千克按原售价的7折售完.售卖结束后，超市决定将盈利的资金捐助给武汉市用于抗击新冠肺炎疫情.那么该超市可以捐助元.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(m^{2})}^{n} \cdot {(m n)}^{3} \div m^{n - 2}$

(2)、解不等式组： ${\begin{array}{l} x + 1 > 0 \\ x \leq \frac{x - 2}{3} + 2 \end{array}$

查看试题解析
20. 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE=OC，连接 CE、OE，连接AE交OD于点F．

(1)、求证：OE=CD

(2)、若菱形ABCD的边长为4，∠ABC=60°，求AE的长．

查看试题解析
21. “泰微课”是学生自主学习近平台，某初级中学共有1200名学生，每人每周学习的数学泰微课都在6至30个之间（含6和30），为进一步了解该校学生每周学习数学泰微课的情况，从三个年级随机抽取了部分学生的相关学习数据，并整理、绘制成统计图如下：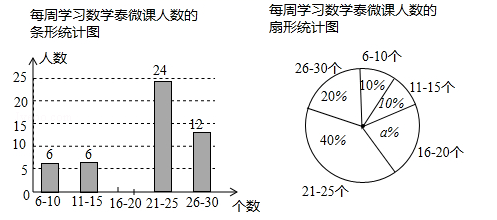

根据以上信息完成下列问题：

(1)、补全条形统计图；

(2)、估计该校全体学生中每周学习数学泰微课在16至30个之间（含16和30）的人数.

查看试题解析
22. 阅读以下材料：对数的创始人是苏格兰数学家纳皮尔（J.Napier，1550年-1617年），纳皮尔发明对数是在指数概念建立之前，直到18世纪瑞士数学家欧拉（Euler，1707年-1783年）才发现指数与对数之间的联系.对数的定义：一般地，若 $a^{x} = N (a > 0 ， a \neq 1)$ ，则 $x$ 叫做以a为底N的对数，记作 $x = \log_{a} N$ .比如指数式 $2^{4} = 16$ 可以转化为 $4 = \log_{2} 16$ ，对数式 $2 = \log_{5} 25$ 可以转化为 $5^{2} = 25$ .我们根据对数的定义可得到对数的一个性质： $\log (M · N) = \log_{a} M +$ $\log_{a} N (a > 0 ， a \neq 1 ， M > 0，N > 0)$ .理由如下：设 $\log_{a} M = m$ ， $\log_{a} N = n$ ，所以 $M = a^{m}$ ， $N = a^{n}$ ，所以 $M N = a^{m} a^{n} = a^{m + n}$ ，由对数的定义得 $m + n = \log_{a} (M + N)$ ，又因为 $m + n = \log_{a} M + \log_{a} N$ ，所以 $\log_{a} (M N) = {log}_{a} M + \log_{a} N$ .解决以下问题：

(1)、将指数 $5^{3} = 125$ 转化为对数式：.

(2)、仿照上面的材料，试证明： $\log_{a} \frac{M}{N} = \log_{a} M - \log_{a} N (a > 0 ， a \neq 1 ， M > 0 ， N > 0)$

(3)、拓展运用：计算 $\log_{3} 2 + \log_{3} 18 - \log_{3} 4 =$ .

查看试题解析
23. 为了做好新冠肺炎疫情期间开学工作，我区某中学用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例；药物释放完毕后，y与x成反比例，如图所示.根据图中提供的信息，解答下列问题：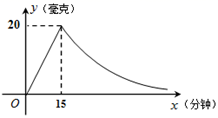

(1)、写出倾倒一瓶药物后，从药物释放开始，y与x之间的两个函数关系式及相应的自变量取值范围；

(2)、据测定，当空气中每立方米的含药量不低于8毫克时，消毒有效，那么倾倒一瓶药物后，从药物释放开始，有效消毒时间是多少分钟？

查看试题解析
24. 如图1，点A是线段BC上一点，△ABD，△AEC都是等边三角形，BE交AD于点M，CD交AE于N.

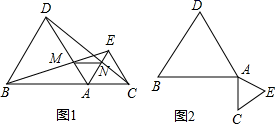(1)、求证：BE=DC；

(2)、求证：△AMN是等边三角形；

(3)、将△ACE绕点A按顺时针方向旋转90°，其它条件不变，在图2中补出符合要求的图形，并判断（1）、（2）两小题结论是否仍然成立，并加以证明.

查看试题解析
25. 新冠肺炎疫情发生后，口罩市场出现热销，小明的爸爸用12000元购进医用外科、N95两种型号的口罩在自家药房销售，销售完后共获利2700元，进价和售价如下表：

品名价格

医用外科口罩

N95口罩

进价（元/袋）

20

30

售价（元/袋）

25

36

(1)、小明爸爸的药房购进医用外科、N95两种型号口罩各多少袋？

(2)、该药房第二次以原价购进医用外科、N95两种型号口罩，购进医用外科口罩袋数不变，而购进N95口罩袋数是第一次的2倍，医用外科口罩按原售价出售，而效果更好的N95口罩打折让利销售，若两种型号的口罩全部售完，要使第二次销售活动获利不少于2460元，每袋N95口罩最多打几折？

查看试题解析
26. 已知：正方形 $A B C D$ 中， $∠ M A N = 45^{\circ}$ ， $∠ M A N$ 绕点 $A$ 顺时针旋转，它的两边分别交 $C B ， D C$ （或它们的延长线）于点 $M ， N$ .
当 $∠ M A N$ 绕点 $A$ 旋转到 $B M = D N$ 时（如图1），易证 $B M + D N = M N$ .

(1)、当 $∠ M A N$ 绕点 $A$ 旋转到 $B M \neq D N$ 时（如图2），线段 $B M \neq D N$ 和 $M N$ 之间有怎样的数量关系？写出猜想，并加以证明.

(2)、当 $∠ M A N$ 绕点 $A$ 旋转到如图3的位置时，线段 $B M \neq D N$ 和 $M N$ 之间又有怎样的数量关系？请直接写出你的猜想.

查看试题解析

品名价格	医用外科口罩	N95口罩
进价（元/袋）	20	30
售价（元/袋）	25	36