北京市延庆区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案中，既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程 $x^{2} - 3 x + 1 = 0$ 的根的情况是（）

A、有两个相等实数根 B、有两个不相等实数根 C、没有实数根 D、无法判断

查看试题解析
3. 一个六边形的内角和等于（）

A、360° B、480° C、720° D、1080°

查看试题解析
4. 在平面直角坐标中，点M（-2，3）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 将一元二次方程x²﹣2x﹣1＝0配方后为（）

A、（x+1）²＝1 B、（x+1）²＝2 C、（x﹣1）²＝2 D、（x﹣1）²＝1

查看试题解析
6. 一次函数 $y = 2 x + b$ 经过点 $(0 ， - 4)$ ，那么b的值为（）

A、-4 B、4 C、8 D、-8

查看试题解析
7. 如图，四边形ABCD的对角线相交于点O ，且互相平分．若添加下列条件，不能判定四边形ABCD为矩形的是（）

A、AC＝BD B、∠DAB＝90° C、AB＝AD D、∠ADC+∠ABC＝180°

查看试题解析
8. 在平面直角坐标系xOy中，如图，四边形ABCD是菱形，∠DAB＝60°，点P是边CD的中点，如果菱形的周长为16，那么点P的坐标是（）

A、（4，4） B、（2，2） C、（ $2 \sqrt{3}$ ，1） D、（ $\sqrt{3}$ ，1）

查看试题解析

二、填空题

9. 一元二次方程 $x^{2} - 3 x = 0$ 的根是．

查看试题解析
10. 函数y= $\sqrt{2 x - 3}$ 中自变量x的取值范围是．

查看试题解析
11. 如图，在Rt△ABC中，点D分别是边AB的中点，若AB＝4，则CD＝.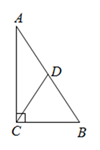

查看试题解析
12. 若关于x的一元二次方程 $x^{2} - 2 x + a = 0$ 的一个根是3，则a的值是．

查看试题解析
13. 写出一个图象经过二、四象限的反比例函数的表达式.（只需写出一个正确的函数表达式即可）

查看试题解析
14. 下图是天安门广场周围的景点分布示意图，若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示人民大会堂的点的坐标为（-2，0），表示王府井的点的坐标为（2，2），则表示故宫的点的坐标是．

查看试题解析
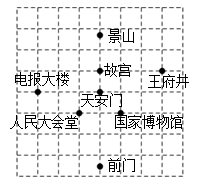15. 关于 $x$ 的一元二次方程 $x^{2} - b x + c = 0$ （ $b \neq 0$ ）有两个相等的实数根，写出一组满足条件的实数b ， c的值：b= ， c= ．

查看试题解析
16. 自2020年1月1日延庆区开展创城以来，积极推广垃圾分类，在垃圾分类指导员的帮助下，居民的投放符合题意率不断提升，分类习惯正在养成．尤其是在5月1日新版《北京市生活垃圾管理条例》实施以来，延庆区城管委为全区从源头上规范垃圾投放，18个街乡镇新配备户用分类垃圾桶20万个，助力推进垃圾分类．下面两张图表是某小区每个月的厨余垃圾量和其他垃圾量．

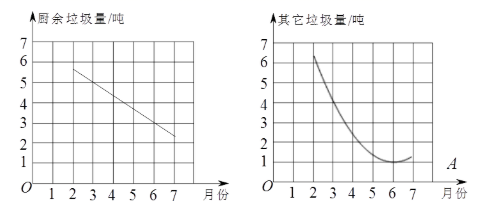(1)、3月份厨余垃圾量比其他垃圾量多吨；

(2)、月份两类垃圾量（单位：吨）的差距最大．

查看试题解析

三、解答题

17. 解方程：

(1)、 $x^{2} - 2 x - 3 = 0$ ．

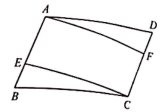
(2)、 $3 x^{2} + 2 x - 1 = 0$ ．

查看试题解析
18. 已知：一次函数的图象经过点A（4，3）和B（-2，0）．

(1)、求这个一次函数的表达式；

(2)、求一次函数与y轴的交点．

查看试题解析
19. 关于x的一元二次方程 $x^{2} - 4 x + k = 0$ 有两个实数根．

(1)、求k的取值范围；

(2)、请选择一个合适的数作为k的值，并求此时方程的根．

查看试题解析
20. 如图， $▱ A B C D$ 中，点 $E$ 、 $F$ 分别在 $A B$ 、 $C D$ 上，且 $B E = D F$ .求证： $A F = E C$ ．

查看试题解析
21. 如图，利用一面墙（墙的长度不限），用20米的篱笆，怎样围成一个面积为50平方米的矩形场地？

查看试题解析
22. 已知：如图，线段AB ， BC ．

(1)、求作：□ABCD（要求尺规作图，保留作图痕迹，不写作法）；

(2)、四边形ABCD是平行四边形的依据是．

查看试题解析
23. 如图，函数 $y = x$ 的图象与函数 $y = \frac{k}{x} (x > 0)$ 的图象相交于点P（1，m）.

(1)、求 $m$ ， $k$ 的值；

(2)、直线 $y = 3$ 与函数 $y = x$ 的图象相交于点A ，与函数 $y = \frac{k}{x} (x > 0)$ 的图象相交于点B ，求线段AB长．

查看试题解析
24. 在矩形ABCD中，点E ，点F分别为边BC ， DA延长线上的点，且CE=AF ，连接AE ， DE ， BF ．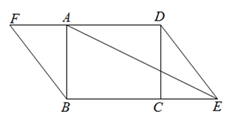

(1)、求证：四边形BEDF是平行四边形；

(2)、若AF=1，AB=2，AD= $\sqrt{5}$ ，求证：AE平分∠DEB ．

查看试题解析
25. 自开展全区读书宣传活动以来，某书店出租店生意非常火爆，为此开设两种租书方式，方式一：零星租书，每本收费1元；方式二：会员卡租书，会员每月交会员费12元，租书费每本0.4元．小彬经常来该店租书，若小彬每月租书数量为x本，每月应付的租书金额为y元．

(1)、分别写出两种租书方式下，y与x之间的函数关系；

(2)、若小彬在一月内为班级租25本书，试问选用哪种租书方式合算？

查看试题解析

26. 有这样一个问题：探究函数

y = x + \frac{1}{x}

的图象与性质．小东根据学习函数的经验，对函数

y = x + \frac{1}{x}

的图象与性质进行了探究．下面是小东的探究过程，请补充完整：

(1)、函数

y = x + \frac{1}{x}

的自变量x的取值范围是；

(2)、下表是y与x的几组对应值．

…

﹣3

﹣2

﹣1

﹣ $\frac{1}{2}$

﹣ $\frac{1}{3}$

$\frac{1}{3}$

$\frac{1}{2}$

…

$- \frac{10}{3}$

$- \frac{5}{2}$

-2

$- \frac{5}{2}$

$\frac{10}{3}$

$\frac{5}{2}$

$\frac{10}{3}$

…

求m的值；

(3)、如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；

(4)、结合函数的图象，写出该函数的其它性质（一条即可）．

查看试题解析

27. 如图，四边形ABCD是正方形，点E是边BC的任意一点，连接AE ，过点B做BH⊥AE ，垂足为H ，交CD于点P ，将线段PC绕着点P逆时针旋转90°得到线段PQ ，连接EQ ．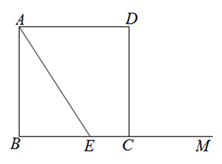

(1)、补全图形；

(2)、写出AE与EQ的数量关系，并加以证明．

查看试题解析
28. 规定：若直线l与图形M有公共点，则称直线l是图形M的关联直线．已知：矩形ABCD的其中三个顶点的坐标为A（t ， 0），B（t+2，0），C（t+2，3）

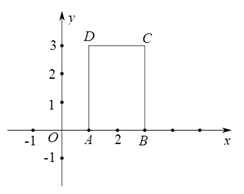(1)、当t=1时，如图以下三个一次函数 $y_{1} = x + 4$ ， $y_{2} = - x + 2$ ， $y_{3} = x + 2$ 中，是矩形ABCD的关联直线；

(2)、已知直线l： $y = x + 2$ ，若直线l是矩形ABCD的关联直线，求t的取值范围；

(3)、如果直线m： $y = t x + 2$ （ $t > 0$ ）是矩形ABCD的关联直线，请直接写出t的取值范围．

查看试题解析