北京市通州区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 下面四个图案中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,矩形ABCD的对角线AC和BD相交于点O , 过点O的直线分别交AD和BC于点E、F , AB=2,BC=3,则图中阴影部分的面积为( )
2. 如图,矩形ABCD的对角线AC和BD相交于点O , 过点O的直线分别交AD和BC于点E、F , AB=2,BC=3,则图中阴影部分的面积为( )
 A、3 B、4 C、5 D、63. 在样本方差的计算公式 中,数字10和20分别表示样本的( )A、容量和方差 B、标准差和平均数 C、容量和平均数 D、平均数和容量4. 直线y=kx+b(k<0)与x轴交于点(3,0),关于x的不等式kx+b>0的解集是( )
A、3 B、4 C、5 D、63. 在样本方差的计算公式 中,数字10和20分别表示样本的( )A、容量和方差 B、标准差和平均数 C、容量和平均数 D、平均数和容量4. 直线y=kx+b(k<0)与x轴交于点(3,0),关于x的不等式kx+b>0的解集是( )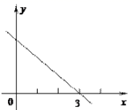 A、x<3 B、x>3 C、x>0 D、x<05. 下列命题中,能判断四边形是矩形的是( )A、对角线相等 B、对角线互相平分 C、对角线相等且互相平分 D、对角线互相垂直6. 在平面直角坐标系中,已知线段AB的两个端点分别是A(- 4 ,-1).B(1,1) 将线段AB平移后得到线段A ’B’,若点A’的坐标为 (-2 , 2 ) ,则点 B’的坐标为( )A、( 3 , 4 ) B、( 4 , 3 ) C、(-1 ,-2 ) D、(-2,-1)7. 方程 的解是( )A、 B、 C、 D、8. 已知正方形轨道 的边长为 小明站在正方形轨道 边的中点 处,操控一辆无人驾驶小汽车,小汽车沿着折线 以每秒 的速度向点 (终点)移动,如果将小汽车到小明的距离设为 将小汽车运动的时间设为 那么 与 之间关系的图象大致是( )
A、x<3 B、x>3 C、x>0 D、x<05. 下列命题中,能判断四边形是矩形的是( )A、对角线相等 B、对角线互相平分 C、对角线相等且互相平分 D、对角线互相垂直6. 在平面直角坐标系中,已知线段AB的两个端点分别是A(- 4 ,-1).B(1,1) 将线段AB平移后得到线段A ’B’,若点A’的坐标为 (-2 , 2 ) ,则点 B’的坐标为( )A、( 3 , 4 ) B、( 4 , 3 ) C、(-1 ,-2 ) D、(-2,-1)7. 方程 的解是( )A、 B、 C、 D、8. 已知正方形轨道 的边长为 小明站在正方形轨道 边的中点 处,操控一辆无人驾驶小汽车,小汽车沿着折线 以每秒 的速度向点 (终点)移动,如果将小汽车到小明的距离设为 将小汽车运动的时间设为 那么 与 之间关系的图象大致是( )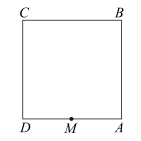 A、
A、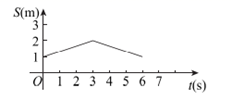 B、
B、 C、
C、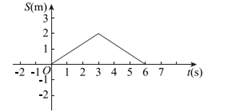 D、
D、
二、填空题
-
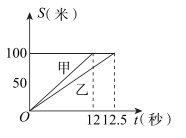
9. 正六边形的内角和为度.10. 关于x的一元二次方程 ,满足 ,那么方程必有一个根是 .11. 甲、乙两人在一次赛跑中,路程 与时间 的关系如图所示,那么可以知道:(1)这是一次米赛跑;(2)乙在这次赛跑中的速度为米/秒.
 12. 在统计学中,样本的方差可以近似地反映总体的 . (填写“集中趋势”、“波动大小”、“最大值”、“平均值”)13. 写出一个图象经过点(-1,-1),且不经过第一象限的函数表达式.14. 如图,在 中, 于点 点 分别是 边的中点,请你在 中添加一个条件: , 使得四边形 是菱形.
12. 在统计学中,样本的方差可以近似地反映总体的 . (填写“集中趋势”、“波动大小”、“最大值”、“平均值”)13. 写出一个图象经过点(-1,-1),且不经过第一象限的函数表达式.14. 如图,在 中, 于点 点 分别是 边的中点,请你在 中添加一个条件: , 使得四边形 是菱形.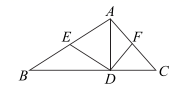 15. 如图, 是 的中线, 把 沿 折叠,使点 落在点 处, 与 的长度比是 .
15. 如图, 是 的中线, 把 沿 折叠,使点 落在点 处, 与 的长度比是 .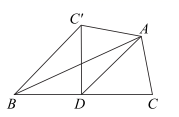 16. 如图,在斜边长为 的等腰直角三角形 中,作内接正方形 ;在等腰直角三角形 中,作内接正方形 ;在等腰直角三角形 中,作内接正方形 ;……;依次作下去,则第 个正方形 的边长是(用含有 的代数式表示)
16. 如图,在斜边长为 的等腰直角三角形 中,作内接正方形 ;在等腰直角三角形 中,作内接正方形 ;在等腰直角三角形 中,作内接正方形 ;……;依次作下去,则第 个正方形 的边长是(用含有 的代数式表示)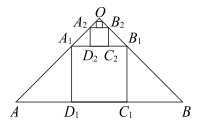
三、解答题
-
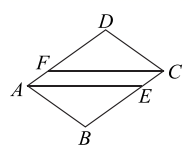
17. 选择恰当的方法解下列一元二次方程.(1)、 ;(2)、 ;(3)、 ;(4)、 .18. 如图,在 中, 平分 交 于点 平分 交 于点 求证:四边形 是平行四边形.
 19. 已知一次函数 的图象经过点 且与正比例函数 的图象相交于点 ,求:
19. 已知一次函数 的图象经过点 且与正比例函数 的图象相交于点 ,求: (1)、a的值;(2)、求一次函数 的表达式;(3)、请你画出这两个函数的图象,并判断当 取何值时, ;(4)、求这两个函数图象与 轴围成的三角形的面积.20. 关于 的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、若方程有一根小于1,求 的取值范围.21. 如图,在▱ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)、a的值;(2)、求一次函数 的表达式;(3)、请你画出这两个函数的图象,并判断当 取何值时, ;(4)、求这两个函数图象与 轴围成的三角形的面积.20. 关于 的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、若方程有一根小于1,求 的取值范围.21. 如图,在▱ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.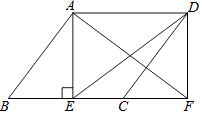 (1)、求证:四边形AEFD是矩形;(2)、若AB=6,DE=8,BF=10,求AE的长.22. 对某班20名学生的每分钟脉搏次数情况测量如下(单位:次): ,按要求回答问题:(1)、补全表格中的数据.
(1)、求证:四边形AEFD是矩形;(2)、若AB=6,DE=8,BF=10,求AE的长.22. 对某班20名学生的每分钟脉搏次数情况测量如下(单位:次): ,按要求回答问题:(1)、补全表格中的数据.分组
频数累计
频数
频率
2
0.1
正

4
0.2
正正正
9
0.15
正正正正
2
0.1
合计
20
1
(2)、根据上边的频数分布表,绘制频数分布直方图. (3)、这个样本的最小值是 , 分组的组距是;(4)、样本中每分钟脉搏次数在 次之间的学生所占的百分比率为 .(5)、样本中落入小组内的数据频率最大,该频率为 .23. 小明在积累了学习函数的经验之后,自主探究学习了一个新函数: .小明首先观察函数表达式,确定此函数的自变量的取值范围,之后列表求值,画出函数图象,研究函数的性质.请你协助小明完成下列问题:
(3)、这个样本的最小值是 , 分组的组距是;(4)、样本中每分钟脉搏次数在 次之间的学生所占的百分比率为 .(5)、样本中落入小组内的数据频率最大,该频率为 .23. 小明在积累了学习函数的经验之后,自主探究学习了一个新函数: .小明首先观察函数表达式,确定此函数的自变量的取值范围,之后列表求值,画出函数图象,研究函数的性质.请你协助小明完成下列问题: (1)、自变量x的取值范围;(2)、列表求值 .请你协助小明补全表格:
(1)、自变量x的取值范围;(2)、列表求值 .请你协助小明补全表格:···
-3
-2
-1
-0.5
-0.1
0.1
0.5
1
2
3
···
···
2
···
(3)、请你画出函数 的大致图象,并试着写出它的两条性质.性质: .24. 要在一个 的照片外侧的四周镶上宽度相同的银边,并且要使银边的面积和照片的面积相等,那么银边的宽应该是多少?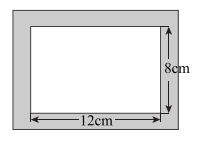 25. 把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
25. 把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.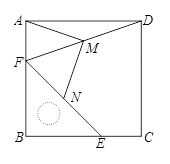
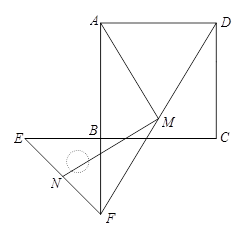 图2
图2图1
(1)、如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接写出结论;(2)、如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.26. 如图,菱形 的边长是 厘米,对角线 相交于点 且 厘米,点 分别在 上,点 从点 出发,以每秒 厘米的速度向终点 运动,点 从点 出发,以每秒 厘米的速度向点 运动,点 移动到点 后,点 停止运动.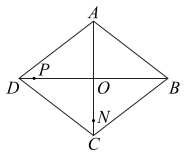 (1)、当运动多少秒时, 的面积是 平方厘米;(2)、如果 的面积为 ,请你写出 关于时间 的函数表达式.
(1)、当运动多少秒时, 的面积是 平方厘米;(2)、如果 的面积为 ,请你写出 关于时间 的函数表达式.