重庆市2020年数学中考定心卷
试卷更新日期:2020-09-14 类型:中考模拟
一、单选题。
-
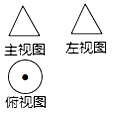
1. 数1,0, ,﹣2中最大的是( )A、1 B、0 C、 D、﹣22. 已知某几何体的三视图如图所示,则该几何体可能是( )
 A、
A、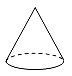 B、
B、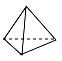 C、
C、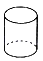 D、
D、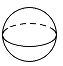 3. 如图.点A,B,C,D,E均在⊙O上.∠BAC=15°,∠CED=30°,则∠BOD的度数为( )
3. 如图.点A,B,C,D,E均在⊙O上.∠BAC=15°,∠CED=30°,则∠BOD的度数为( ) A、45° B、60° C、75° D、90°4. 下列各数中,介于 和 之间的是( )A、2 B、3 C、4 D、55. 在党和国家的领导下,全国人民的共同努力,全国疫情进入尾声,各行各业纷纷复工复产,经济形势也越来越好.下列调查中,不适合用抽样调查方式的是( )A、调查全国餐饮企业员工的复工情况. B、调查全国医用口罩日生产量 C、北京市高三学生全面复学,调查和检测某学校高三学生和老师的体温 D、调查疫情期间北京地铁的客流量6. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、
A、45° B、60° C、75° D、90°4. 下列各数中,介于 和 之间的是( )A、2 B、3 C、4 D、55. 在党和国家的领导下,全国人民的共同努力,全国疫情进入尾声,各行各业纷纷复工复产,经济形势也越来越好.下列调查中,不适合用抽样调查方式的是( )A、调查全国餐饮企业员工的复工情况. B、调查全国医用口罩日生产量 C、北京市高三学生全面复学,调查和检测某学校高三学生和老师的体温 D、调查疫情期间北京地铁的客流量6. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、 B、
B、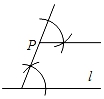 C、
C、 D、
D、 7. 《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问若每日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34 685个字,设他第一天读x个字,则下面所列方程正确的是( ).A、x+2x+4x=34 685 B、x+2x+3x=34 685 C、x+2x+2x=34 685 D、x+ x+ x=34 6858. 一天,小战和同学们一起到操场测量学校旗杆高度,他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°,然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°(身高忽略不计).已知斜坡CD坡度i=1:2.4,坡长为2.6米,旗杆AB所在旗台高度EF为1.4米,旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为( )米.
7. 《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问若每日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34 685个字,设他第一天读x个字,则下面所列方程正确的是( ).A、x+2x+4x=34 685 B、x+2x+3x=34 685 C、x+2x+2x=34 685 D、x+ x+ x=34 6858. 一天,小战和同学们一起到操场测量学校旗杆高度,他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°,然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°(身高忽略不计).已知斜坡CD坡度i=1:2.4,坡长为2.6米,旗杆AB所在旗台高度EF为1.4米,旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
 A、10.2 B、9.8 C、11.2 D、10.89. 已知点A(-1,3),点B(-1,-4),若常数a使得一次函数y=ax+1与线段AB有交点,且使得关于x的不等式组 无解,则所有满足条件的整数a的个数为( )A、3 B、4 C、5 D、610. 如图, 中, ,点 在边 上,且满足 , 为线段 的中点,若 , ,则 ( )
A、10.2 B、9.8 C、11.2 D、10.89. 已知点A(-1,3),点B(-1,-4),若常数a使得一次函数y=ax+1与线段AB有交点,且使得关于x的不等式组 无解,则所有满足条件的整数a的个数为( )A、3 B、4 C、5 D、610. 如图, 中, ,点 在边 上,且满足 , 为线段 的中点,若 , ,则 ( ) A、 B、 C、 D、611. 如图,点A,B在反比例函数 的图象上,点C,D在反比例函数 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )
A、 B、 C、 D、611. 如图,点A,B在反比例函数 的图象上,点C,D在反比例函数 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )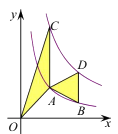 A、4 B、3 C、2 D、12. 下列说法:
A、4 B、3 C、2 D、12. 下列说法:若一元二次方程 有一个根是 ,则代数式 的值是 若 ,则 是一元二次方程 的一个根 若 ,则一元二次方程 有不相等的两个实数根 当m取整数 或1时,关于x的一元二次方程 与 的解都是整数.其中正确的有( )
A、1个 B、2个 C、3个 D、4个二、填空题。
-
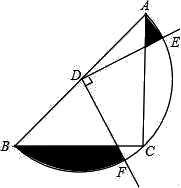
13. 用科学记数法表示:0.0000036=。14. 从1.2.3.4四个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程ax2+4x+c=0有实数解的概率为15. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是 .
 16. A、B两地之间有一修理厂C,一日小海和王陆分别从A、B两地同时出发相向而行,王陆开车,小海骑摩托.二人相遇时小海的摩托车突然出故障无法前行,王陆决定将小海和摩托车一起送回到修理厂C后再继续按原路前行,王陆到达A地后立即返回B地,到B地后不再继续前行,等待小海前来(装载摩托车时间和掉头时间忽略不计),整个行驶过程中王陆速度不变,而小海在修理厂花了十分钟修好摩托车,为了赶时间,提速 前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有km.
16. A、B两地之间有一修理厂C,一日小海和王陆分别从A、B两地同时出发相向而行,王陆开车,小海骑摩托.二人相遇时小海的摩托车突然出故障无法前行,王陆决定将小海和摩托车一起送回到修理厂C后再继续按原路前行,王陆到达A地后立即返回B地,到B地后不再继续前行,等待小海前来(装载摩托车时间和掉头时间忽略不计),整个行驶过程中王陆速度不变,而小海在修理厂花了十分钟修好摩托车,为了赶时间,提速 前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有km. 17. 如图,在矩形纸片ABCD中,AB=8,BC=6,点E是AD的中点,点F是AB上一动点.将△AEF沿直线EF折叠,点A落在点A'处.在EF上任取一点G,连接GC,GA',CA’,则△CGA'的周长的最小值为.
17. 如图,在矩形纸片ABCD中,AB=8,BC=6,点E是AD的中点,点F是AB上一动点.将△AEF沿直线EF折叠,点A落在点A'处.在EF上任取一点G,连接GC,GA',CA’,则△CGA'的周长的最小值为.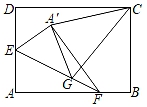 18. “双11”当天,重庆顺风快递公司出动所有车辆分上午、下午两批往成都送件,该公司共有甲、乙、丙三种车型,其中甲型车数量占公司车辆总数的 ,乙型车辆是丙型车数量的2倍,上午安排甲车数量的 ,乙车数量的 ,丙车数量的 进行运输,且上午甲、乙、丙三种车型每辆载货量分别为15吨,10吨,20吨,则上午刚好运完当天全部快件重量的 ;下午安排剩下的所有车辆运输完当天剩下的所有快件,且下午甲、乙、丙三种车型每辆载货量分别不得超过20吨,12吨,16吨,下午乙型车实际载货量为下午甲型车每辆实际载货量的 .已知同种货车每辆的实际载货量相等,甲、乙、丙三种车型每辆车下午的运输成本分别为50元/吨,90元/吨,60元/吨.则下午运输时,一辆甲种车、一辆乙种车、一辆丙种车总的运输成本最少为元.
18. “双11”当天,重庆顺风快递公司出动所有车辆分上午、下午两批往成都送件,该公司共有甲、乙、丙三种车型,其中甲型车数量占公司车辆总数的 ,乙型车辆是丙型车数量的2倍,上午安排甲车数量的 ,乙车数量的 ,丙车数量的 进行运输,且上午甲、乙、丙三种车型每辆载货量分别为15吨,10吨,20吨,则上午刚好运完当天全部快件重量的 ;下午安排剩下的所有车辆运输完当天剩下的所有快件,且下午甲、乙、丙三种车型每辆载货量分别不得超过20吨,12吨,16吨,下午乙型车实际载货量为下午甲型车每辆实际载货量的 .已知同种货车每辆的实际载货量相等,甲、乙、丙三种车型每辆车下午的运输成本分别为50元/吨,90元/吨,60元/吨.则下午运输时,一辆甲种车、一辆乙种车、一辆丙种车总的运输成本最少为元.三、解答题
-
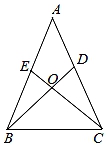
19. 计算:(1)、计算:tan45°+( ﹣ )0﹣(﹣ )-2+| ﹣2|.(2)、 ÷ ﹣20. 如图,已知AB=AC,AD=AE,BD和CE相交于点O.
 (1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.21. 为了增强学生的疫情防控意识,响应“停课不停学”号召,某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校2500名学生都参加的网上测试.阅卷后,教务处随机抽取了100份答卷进行分析统计,发现考试成绩( 分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
(1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.21. 为了增强学生的疫情防控意识,响应“停课不停学”号召,某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校2500名学生都参加的网上测试.阅卷后,教务处随机抽取了100份答卷进行分析统计,发现考试成绩( 分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:分数段(分)
频数(人)
频率
0.1
18
0.18
35
0.35
12
0.12
合计
100
1
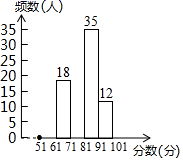 (1)、填空: , , ;(2)、将频数分布直方图补充完整;(3)、该校对成绩为 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为 ,请你估算全校获得二等奖的学生人数;(4)、结合调查的情况,为了提高疫情防控意识,请你给学校提一条合理性建议.22. 小邱同学根据学习函数的经验,研究函数y= 的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
(1)、填空: , , ;(2)、将频数分布直方图补充完整;(3)、该校对成绩为 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为 ,请你估算全校获得二等奖的学生人数;(4)、结合调查的情况,为了提高疫情防控意识,请你给学校提一条合理性建议.22. 小邱同学根据学习函数的经验,研究函数y= 的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.x
1
3
4
5
6
…
y
﹣1
﹣2
﹣3.4
﹣7.5
2.4
1.4
1
0.8
…
 (1)、函数y= 的自变量x的取值范围是;(2)、在图中补全当1≤x<2的函数图象;(3)、观察图象,写出该函数的一条性质:;(4)、若关于x的方程 =x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是.23. 数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则”.
(1)、函数y= 的自变量x的取值范围是;(2)、在图中补全当1≤x<2的函数图象;(3)、观察图象,写出该函数的一条性质:;(4)、若关于x的方程 =x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是.23. 数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则”.材料一:平方运算和开方运算是互逆运算.如a2±2ab+b2=(a±b)2 , 那么 ,如何将双重二次根式 化简.我们可以把 转化为 完全平方的形式,因此双重二次根式 得以化简.
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y’)给出如下定义:若 则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).问题:
(1)、点 的“横负纵变点”为 , 点 的“横负纵变点”为;(2)、化简: ;(3)、已知a为常数(1≤a≤2),点M( ,m)是关于x的函数 图像上的一点,点M’是点M的“横负纵变点”,求点M’的坐标.24. 近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.(1)、从去年年底至今年3月20日,猪肉价格不断走高,3月20日比去年年底价格上涨了60%.某市民在今年3月20日购买2.5千克猪肉至少要花200元钱,那么去年年底猪肉的最低价格为每千克多少元?(2)、3月20日,猪肉价格为每千克60元,3月21日,某市决定投入储备猪肉并规定其销售价在每千克60元的基础上下调a%出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克60元的情况下,该天的两种猪肉总销量比3月20日增加了a%,且储备猪肉的销量占总销量的 ,两种猪肉销售的总金额比3月20日提高了 ,求a的值.25. 如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC. (1)、直接写出点A的坐标,并求直线l的函数表达式(其中k、b用含a的式子表示);(2)、点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为 ,求a的值;(3)、设P是抛物线的对称轴上的一点,点Q在抛物线上,当以点A、D、P、Q为顶点的四边形为矩形时,请直接写出点P的坐标.26. 已知正方形ABCD,点M边AB的中点.(1)、如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
(1)、直接写出点A的坐标,并求直线l的函数表达式(其中k、b用含a的式子表示);(2)、点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为 ,求a的值;(3)、设P是抛物线的对称轴上的一点,点Q在抛物线上,当以点A、D、P、Q为顶点的四边形为矩形时,请直接写出点P的坐标.26. 已知正方形ABCD,点M边AB的中点.(1)、如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
①求证:BE=CF;
②求证:BE2=BC•CE.
(2)、如图2,在边BC上取一点E,满足BE2=BC•CE,连接AE交CM于点G,连接BG并延长CD于点F,直接写出tan∠CBF的值.