湖北省襄阳市襄城区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、选择题

1. 在实数π ， $- \frac{22}{7}$ ， $\sqrt{9}$ ， $\sqrt[3]{8}$ 中，是无理数的是（）

A、p B、 $\sqrt{9}$ C、 $- \frac{22}{7}$ D、 $\sqrt[3]{8}$

查看试题解析
2. 如图， $∠ B A C = 90 °$ ， $A D ⊥ B C$ 于点D，点C到AD的距离是下列哪条线段的长度 $($ $)$

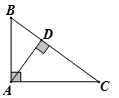A、AC B、BC C、CD D、AD

查看试题解析
3. 81的算术平方根是 $()$

A、 3 B、-3 C、-9 D、9

查看试题解析
4. 若将 $- \sqrt{3}$ ， $\sqrt{5}$ ， $\sqrt{17}$ 表示在数轴上，则其中能被如图所示的墨迹覆盖的数是 $()$ .

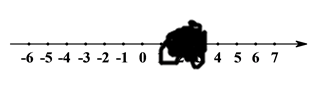A、 $\sqrt{5}$ B、 $- \sqrt{3}$ C、 $\sqrt{17}$ D、都不可能

查看试题解析
5. 下列方程组中，是二元一次方程组的是 $()$

A、 ${\begin{array}{l} x y = 1 \\ x + y = 2 \end{array}$ B、 ${\begin{array}{l} x + 3 y = 2 \\ y + 3 z = 14 \end{array}$ C、 ${\begin{array}{l} x - 2 z = 0 \\ x + y = 4 \end{array}$ D、 ${\begin{array}{l} 5 x - 2 y = 2 \\ x + y = 4 \end{array}$

查看试题解析
6. 若两条直线被第三条直线所截，有一对同位角相等，则其中一对同旁内角的角平分线（）

A、互相垂直 B、互相平行 C、相交或平行 D、不相等

查看试题解析
7. 如图，两只蚂蚁以相同的速度沿两条不同的路径，同时从A出发爬到B，则（）

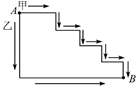A、乙比甲先到 B、甲和乙同时到 C、甲比乙先到 D、无法确定

查看试题解析
8. 下列调查中，最适合采用全面调查（普查）方式的是（）

A、对重庆市居民日平均用水量的调查 B、对一批LED节能灯使用寿命的调查 C、对重庆新闻频道“天天630”栏目收视率的调查 D、对某校九年级（1）班同学的身高情况的调查

查看试题解析
9. 若 $a < 0$ ，则关于x的不等式 $a x + b < 0$ 的解集 $()$

A、 $x > \frac{b}{a}$ B、 $x < \frac{b}{a}$ C、 $x > - \frac{b}{a}$ D、 $x < - \frac{b}{a}$

查看试题解析
10. 下列说法中，正确的个数有（）
（1）两条直线被第三条直线所截，内错角相等；（2）对顶角相等；（3）同一平面内，两条直线的位置关系有：相交，垂直和平行三种；（4）同一平面内，不相交的两条直线一定平行.

A、2个 B、3个 C、4个 D、1个

查看试题解析

二、填空题

11. 如果点P（m+1，m+3）在y轴上，则m= ．

查看试题解析
12. 如图CD⊥AB于D，EF⊥AB于F，∠DGC=105°，∠BCG=75°，则∠1+∠2=.

查看试题解析
13. 二元一次方程组 ${\begin{array}{l} x + y = 6 \\ 2 x + y = 7 \end{array}$ 的解为．

查看试题解析
14. 将点P向左平移2个单位长度，再向上平移1个单位长度得到 $Q (- 1, 3)$ ，则点P的坐标是.

查看试题解析
15. 在同一平面内，直线AB与直线CD相交于点O，∠BOC：∠BOD＝4：5，射线OE⊥CD，则∠BOE的度数为.

查看试题解析
16. 如图，已知AE//CD，BC⊥CD于C，若∠A＝28°，则∠ABC＝ $° .$

查看试题解析

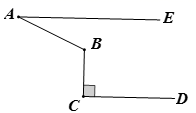
三、解答题

17. 解不等式 $x - 2 (x - 1) > 0$ ，并将它的解集在数轴上表示出来．

查看试题解析
18. 计算： $\sqrt{81} + \sqrt[3]{- 64} + | 2 - \sqrt{3} | + | 1 - \sqrt{3} |$

查看试题解析
19. 解方程组： ${\begin{array}{l} 4 x - 3 y = 14 \\ 5 x + 3 y = 31 \end{array}$

查看试题解析
20. 如图， $△ A B C$ 在方格纸中

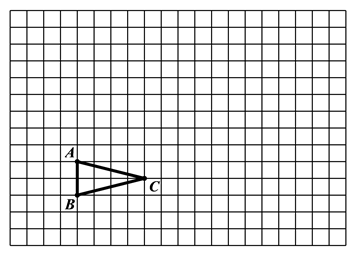
（ 1 ）请在方格纸上建立平面直角坐标系，使点A，B的坐标分别为 $(2 ， 3)$ ， $(2 ， 1)$ ；

（ 2 ）将 $△ A B C$ 平移至 $△ A' B' C$ ，使 $A'$ 的坐标为 $(4 ， 7)$ ，画出平移后的图形 $△ A' B' C'$ .

查看试题解析
21. 如图，已知 $A D ⊥ B C$ 于点D，点E在AB上， $E F ⊥ B C$ 于点F， $∠ 1 = ∠ 2$ ，试说明 $D E / / A C$ .

查看试题解析
22.
某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况，随机抽查部分学生做了一次问卷调查，要求学生选出自己最喜欢的一个版面，将调查数据进行了整理、绘制成部分统计图如下：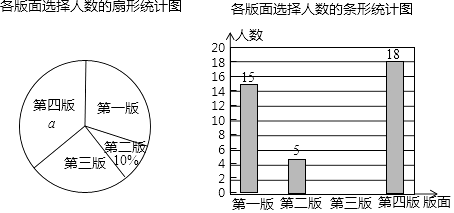
请根据图中信息，解答下列问题：

(1)、该调查的样本容量为， a=%，“第一版”对应扇形的圆心角为°；

(2)、请你补全条形统计图；

(3)、若该校有1000名学生，请你估计全校学生中最喜欢“第三版”的人数．

查看试题解析
23. 某中学组织八年级同学参加校外活动，原计划租用45座客车若干辆，但有15人没有座位；如果租用同样数量的60座客车，则多出一辆，且其余客车恰好坐满.已知45座客车，60座客车日租金分别为220元 $/$ 辆，300元 $/$ 辆.

(1)、设原计划租45座客车x辆，八年级有y人，则 $y =$ $($ 用含x的式子表示 $)$ ；若租用60座客车，则 $y =$ $($ 用含x的式子表示 $)$ ；

(2)、八年级学生有多少人？

(3)、若同时租用两种型号的客车，且要使每个同学都有座位，每辆客车恰好坐满.设租45座客车x辆，租60座客车y辆，问有几种租车方案？

查看试题解析
24. 某工厂现有甲种原料3600kg，乙种原料2410kg，计划利用这两种原料生产A，B两种产品共500件，产品每月均能全部售出．已知生产一件A产品需要甲原料9kg和乙原料3kg；生产一件B种产品需甲种原料4kg和乙种原料8kg．

(1)、设生产x件A种产品，写出x应满足的不等式组．

(2)、问一共有几种符合要求的生产方案？并列举出来．

(3)、若有两种销售定价方案，第一种定价方案可使A产品每件获得利润1.15万元，B产品每件获得利润1.25万元；第二种定价方案可使A和B产品每件都获得利润1.2万元；在上述生产方案中哪种定价方案盈利最多？（请用数据说明）

查看试题解析