北京市门头沟区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,以下各点坐标属于第二象限的点的坐标为( )A、(2,0) B、(﹣1,2) C、(0,2) D、(2,﹣1)2. 已知一个多边形的内角和是360°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形3. 关于x的方程 是一元二次方程,则( )A、m=﹣3 B、m=2 C、m=3 D、m=±34. 下列图象中,y是x的函数的是( )A、
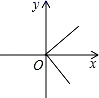 B、
B、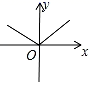 C、
C、 D、
D、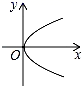 5. 下面图形中是中心对称但不一定是轴对称图形的是( )A、平行四边形 B、长方形 C、菱形 D、正方形6. 方差是表示一组数据的( )A、平均水平 B、数据个数 C、最大值或最小值 D、波动大小7. 关于x的一元二次方程(a﹣2)x2+x+a2﹣4=0的一个根是0,则a的值是( )A、0 B、2 C、﹣2 D、2或﹣28. 甲、乙二人约好沿同一路线去某地集合进行宣传活动,如图,是甲、乙二人行走的图象,点O代表的是学校,x表示的是行走时间(单位:分),y表示的是与学校的距离(单位:米),最后都到达了目的地,根据图中提供的信息,下面有四个推断:
5. 下面图形中是中心对称但不一定是轴对称图形的是( )A、平行四边形 B、长方形 C、菱形 D、正方形6. 方差是表示一组数据的( )A、平均水平 B、数据个数 C、最大值或最小值 D、波动大小7. 关于x的一元二次方程(a﹣2)x2+x+a2﹣4=0的一个根是0,则a的值是( )A、0 B、2 C、﹣2 D、2或﹣28. 甲、乙二人约好沿同一路线去某地集合进行宣传活动,如图,是甲、乙二人行走的图象,点O代表的是学校,x表示的是行走时间(单位:分),y表示的是与学校的距离(单位:米),最后都到达了目的地,根据图中提供的信息,下面有四个推断:①甲、乙二人第一次相遇后,停留了10分钟;②甲先到达的目的地;③甲在停留10分钟之后提高了行走速度;④甲行走的平均速度要比乙行走的平均速度快.所有正确推断的序号是( )
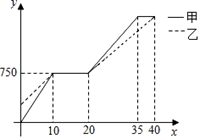 A、①② B、①②③ C、①③④ D、①②④
A、①② B、①②③ C、①③④ D、①②④二、填空题
-
9. 函数 自变量 的取值范围是 .
10. 已知平行四边形邻边之比是1:2,周长是18,则较短的边的边长是 .11. 写出一个一元二次方程,使其中一个根是2,这个方程可以是 .12. 有一组样本容量为20的数据,分别是:7、10、8、14、9、7、12、11、10、8、13、10、8、11、10、9、12、9、13、11,那么该样本数据落在范围8.5~10.5内的频率是 .13. 点A(﹣2,﹣4)到x轴的距离为 .14. 如图,在平行四边形ABCD中,ED=2,BC=5,∠ABC的平分线交AD于点E , 则CD的长为 .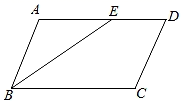 15. 已知一次函数表达式为y=x+2,该图象与坐标轴围成的三角形的面积为 .16. 如图所示,菱形ABCD , 在边AB上有一动点E , 过菱形对角线交点O作射线EO与CD边交于点F , 线段EF的垂直平分线分别交BC、AD边于点G、H , 得到四边形EGFH , 点E在运动过程中,有如下结论:
15. 已知一次函数表达式为y=x+2,该图象与坐标轴围成的三角形的面积为 .16. 如图所示,菱形ABCD , 在边AB上有一动点E , 过菱形对角线交点O作射线EO与CD边交于点F , 线段EF的垂直平分线分别交BC、AD边于点G、H , 得到四边形EGFH , 点E在运动过程中,有如下结论:①可以得到无数个平行四边形EGFH;
②可以得到无数个矩形EGFH;
③可以得到无数个菱形EGFH;
④至少得到一个正方形EGFH .
所有正确结论的序号是 .
 17. 阅读下面材料:
17. 阅读下面材料:在数学课上,老师提出如下问题:
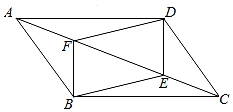
已知:如图,四边形ABCD是平行四边形.
求作:菱形AECF , 使点E , F分别在BC , AD上.

小军的作法如下:
①连接AC;
②作AC的垂直平分线EF分别交BC , AD于E , F;
③连接AE , CF .
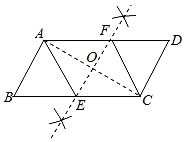
所以四边形AECF是菱形.
老师说:“小军的作法符合题意.”以下是一种证明思路,请结合作图过程补全填空,
由作图和已知可以得到:△AOF≌△COE(依据:);
∴AF=CE;
∵;
∴四边形AECF是平行四边形(依据:);
∵EF垂直平分AC;
∴(依据:);
∴四边形AECF是菱形.
18. 已知:一次函数y=(2﹣m)x+m﹣3.(1)、如果此函数图象经过原点,那么m应满足的条件为;(2)、如果此函数图象经过第二、三、四象限,那么m应满足的条件为;(3)、如果此函数图象与y轴交点在x轴下方,那么m应满足的条件为;(4)、如果此函数图象与y轴交点到x轴的距离为2,那么m应满足的条件为 .19. 阅读理解:由所学一次函数知识可知,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与x轴交点横坐标,是一元一次方程kx+b=0(k≠0)的解;在x轴下方的图象所对应的x的所有值是kx+b<0(k≠0)的解集,在x轴上方的图象所对应的x的所有值是kx+b>0(k≠0)的解集.例,如图1,一次函数kx+b=0(k≠0)的图象与x轴交于点A(1,0),则可以得到关于x的一元一次方程kx+b=0(k≠0)的解是x=1;kx+b<0(k≠0)的解集为x<1.结合以上信息,利用函数图象解决下列问题:
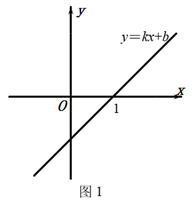
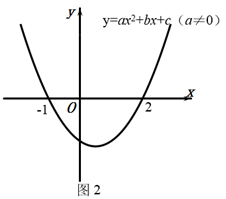 (1)、通过图1可以得到kx+b>0(k≠0)的解集为;(2)、通过图2可以得到
(1)、通过图1可以得到kx+b>0(k≠0)的解集为;(2)、通过图2可以得到①关于x的一元二次方程ax2+bx+c=0(a≠0)的解为;
②关于x的不等式ax2+bx+c>0(a≠0)的解集为 .
三、解答题
-
20. 用配方法解方程x2﹣2x﹣1=0.21. 判断方程4x2﹣1=3x是否有解,如果有,请求出该方程的解;如果没有,请说明理由.22. 如图,已知在▱ABCD中,E、F是对角线AC上的两点,且DF∥BE . 求证:四边形BEDF是平行四边形.
 23. 直线y= x+2与x轴、y轴分别交于点A和点B , 点C在线段AB上,点C到x轴的距离为1.
23. 直线y= x+2与x轴、y轴分别交于点A和点B , 点C在线段AB上,点C到x轴的距离为1. (1)、点B的坐标为;点C的坐标为;(2)、点P为线段OA上的一动点,当PC+PB最小时,画出示意图并直接写出最小值.24. 如图,在矩形ABCD中,点E是BC上一点,DF=DC , DF⊥AE于F .
(1)、点B的坐标为;点C的坐标为;(2)、点P为线段OA上的一动点,当PC+PB最小时,画出示意图并直接写出最小值.24. 如图,在矩形ABCD中,点E是BC上一点,DF=DC , DF⊥AE于F .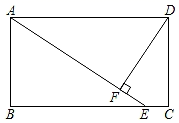 (1)、求证:AE=BC;(2)、如果AB=3,AF=4,求EC的长.25. 垃圾分类全民开始行动,为了了解学生现阶段对于“垃圾分类”知识的掌握情况,某校组织全校1000名学生进行垃圾分类答题测试,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
(1)、求证:AE=BC;(2)、如果AB=3,AF=4,求EC的长.25. 垃圾分类全民开始行动,为了了解学生现阶段对于“垃圾分类”知识的掌握情况,某校组织全校1000名学生进行垃圾分类答题测试,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:分组/分
频数
频率
50≤x<60
12
0.12
60≤x<70
a
0.10
70≤x<80
32
0.32
80≤x<90
20
0.20
90≤x≤100
c
b
合计
100
1.00
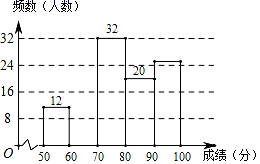 (1)、表中的a= , b= , c=;(2)、把上面的频数分布直方图补充完整;(3)、如果成绩达到80及80分以上者为测试通过,那么请你估计该校测试通过的学生大约有多少人;对于此结果你有什么建议.26. 如图,在平面直角坐标系xOy中,我们把横纵坐标都为整数的点叫做“整点坐标”,正比例函数y=kx(k≠0)的图象与直线x=3及x轴围成三角形.
(1)、表中的a= , b= , c=;(2)、把上面的频数分布直方图补充完整;(3)、如果成绩达到80及80分以上者为测试通过,那么请你估计该校测试通过的学生大约有多少人;对于此结果你有什么建议.26. 如图,在平面直角坐标系xOy中,我们把横纵坐标都为整数的点叫做“整点坐标”,正比例函数y=kx(k≠0)的图象与直线x=3及x轴围成三角形. (1)、正比例函数y=kx(k≠0)图象过点(1,1);
(1)、正比例函数y=kx(k≠0)图象过点(1,1);①k的值为;
②该三角形内的“整点坐标”有个;
(2)、如果在x轴上方由已知形成的三角形内有3个“整点坐标”,求k的取值范围.27. 如图,在正方形ABCD中,E是边AB上的一动点(不与点A , B重合),连接DE , 将线段ED绕点E顺时针旋转90°得到线段EF , 连接BF . (1)、按已知补全图形;(2)、用等式表示线段BF与AE的数量关系并证明.(提示:可以通过旋转的特征构造全等三角形,从而可以得到线段间的数量关系,再去发现生成的特殊的三角形,问题得以解决)28. 我们给出如下定义:在平面直角坐标系xOy中,对于任意一点P(x , y)如果满足x=2|y|,我们就把点P(x , y)称作“特征点”.
(1)、按已知补全图形;(2)、用等式表示线段BF与AE的数量关系并证明.(提示:可以通过旋转的特征构造全等三角形,从而可以得到线段间的数量关系,再去发现生成的特殊的三角形,问题得以解决)28. 我们给出如下定义:在平面直角坐标系xOy中,对于任意一点P(x , y)如果满足x=2|y|,我们就把点P(x , y)称作“特征点”. (1)、在直线x=4上的“特征点”为;(2)、一次函数y=x﹣2的图象上的“特征点”为;(3)、有线段MN , 点M、N的坐标分别为M(1,a)、N(4,a),如果线段MN上始终存在“特征点”,求a的取值范围.
(1)、在直线x=4上的“特征点”为;(2)、一次函数y=x﹣2的图象上的“特征点”为;(3)、有线段MN , 点M、N的坐标分别为M(1,a)、N(4,a),如果线段MN上始终存在“特征点”,求a的取值范围.