北京市丰台区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四组线段中，能作为直角三角形三条边的是（）

A、3，4，5 B、6，8，11 C、1，2， $\sqrt{2}$ D、5，12，15

查看试题解析
2. 下列实数中，方程 $x^{2} - x = 0$ 的根是（）

A、-2 B、-1 C、1 D、2

查看试题解析
3. 某服装店店主统计一段时间内某品牌男衬衫39号，40号，41号，43号的销售情况如下表所示．

男衬衫号码

39号

40号

41号

42号

43号

销售数量/件

3

12

21

9

5

他决定进货时，增加41号衬衫的进货数量，影响该店主决策的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
4. 解一元二次方程x²＋4x－1＝0，配方正确的是（）

A、 ${(x + 2)}^{2} = 3$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 5$ D、 ${(x - 2)}^{2} = 5$

查看试题解析
5. 如图，在矩形ABCD中，对角线AC ， BD交于点O ，若 $∠ A O D = 120^{°}$ ， $B D = 6$ ．则AB的长为（）

A、 $\frac{3}{2}$ B、3 C、 $2 \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
6. 下列各曲线中，不表示 $y$ 是 $x$ 的函数的是（）

A、 B、 C、 D、

查看试题解析
7. 已知小明家、公园、文具店在同一条直线上．小明从家去公园，在公园锻炼了一段时间后又到文具店买文具，然后再回家．下图反映了这个过程中，小明离家的距离 $y$ 与时间 $x$ 之间的对应关系．下列说法错误的是（）

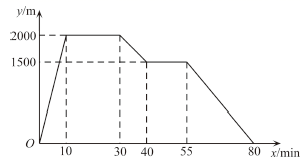A、小明家距离公园2000m； B、公园距离文具店500m； C、小明在文具店买文具花了15min； D、小明从公园到文具店的平均速度为 $60 m / min$ ．

查看试题解析
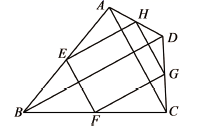8. 如图，点 $E$ ， $F$ ， $G$ ， $H$ 分别是四边形 $A B C D$ 边 $A B$ ， $B C$ ， $C D$ ， $D A$ 的中点．若 $A C ⊥ B D$ ，则四边形 $E F G H$ 的形状为（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
9. 如图，在平面直角坐标系 $x O y$ 中，四边形 $A B C D$ 是菱形， $∠ A B C = 120 °$ ，点 $B$ 的坐标为 $(0 ， - 2)$ ，则菱形ABCD的面积为（）

A、16 B、32 C、 $8 \sqrt{3}$ D、 $16 \sqrt{3}$

查看试题解析
10. 在平面直角坐标系 $x O y$ 中，已知点 $A (- 1, 2)$ ， $B (3, 2)$ ，若一次函数 $y = - x + b$ 的图象与线段 $A B$ 有交点，则 $b$ 的取值范围是（）

A、 $b \leq - 1$ 或 $b \geq 3$ B、 $- 1 \leq b \leq 3$ C、 $b \leq 1$ 或 $b \geq 5$ D、 $1 \leq b \leq 5$

查看试题解析

二、填空题

11. 在 $▱ A B C D$ 中，若 $∠ A + ∠ C = 100 °$ ，则 $∠ A =$ ．

查看试题解析
12. 请写出一个过点（0，1），且y随着x的增大而减小的一次函数解析式．

查看试题解析
13. 在某次体质健康测试中，将学生分两组进行测试，两组学生测试成绩的折线统计图如下，设第一组学生成绩的方差为 $s_{1}^{2}$ ，第二组学生成绩的方差为 $s_{2}^{2}$ ，则 $s_{1}^{2}$ $s_{2}^{2}$ ．（填“ $>$ ”，“ $=$ ”或“ $<$ ”）

查看试题解析
14. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $D$ 是 $A B$ 的中点，若 $C D = 3$ ，则 $A B$ 的长度为．

查看试题解析
15. 为了解某校八年级学生在延期开学期间每天学习时间的情况，随机调查了该校八级 $20$ 名学生，将所得数据整理并制成下表．

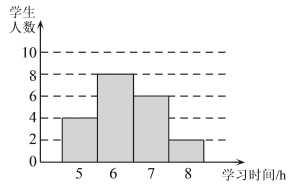
据此估计该校八年级学生每天的平均学习时间大约是 $h$ ．

查看试题解析
16. 下表为研究弹簧长度与所挂物体质量关系的实验表格．

所挂物体质量 $x (kg)$

1

2

3

4

5

弹簧长度 $y (cm)$

10

12

14

16

18

则弹簧不挂物体时的长度为 $cm$ ．当所挂物体质量为 $3.5 kg$ 时，弹簧比原来伸长了 $cm$ ．

查看试题解析
17. 如图，学校需要测量旗杆的高度．同学们发现系在旗杆顶端的绳子垂到了地面，并多出了一段．同学们首先测量了多出的这段绳子长度为 $1 m$ ，然后将这根绳子拉直，当绳子的另一端和地面接触时，绳子与旗杆的底端距离恰好为 $5 m$ ，利用勾股定理求出旗杆的高度约为 m．

查看试题解析
18. 如图，在平面直角坐标系 $x O y$ 中，直线 $l_{1}$ ， $l_{2}$ 分别是函数 $y = k_{1} x + b_{1}$ 和 $y = k_{2} x + b_{2}$ 的图象，则关于 $x$ 的不等式 $k_{1} x + b_{1} > k_{2} x + b_{2}$ 的解集为．若 $m$ ， $n$ 分别满足方程 $k_{1} x + b_{1} = 1$ 和 $k_{2} x + b_{2} = 1$ ，则 $m$ ， $n$ 的大小关系是 $m$ $n$ ．（填或“ $>$ ”“ $=$ ”“ $<$ ”）

查看试题解析

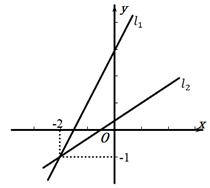
三、未知

19. 解方程：x²-6x+5=0

查看试题解析

四、解答题

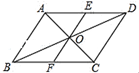
20. 在平面直角坐标系 $x O y$ 中，已知一次函数 $y = k x + b (k \neq 0)$ 的图象过点 $(1 ， 3)$ ， $(- 1 ， 1)$ ．

(1)、求一次函数的解析式；

(2)、一次函数图象与x轴，y轴分别交于点 $A$ ， $B$ ，求 $△ O A B$ 的面积．

查看试题解析
21. 如图，在▱ABCD 中，对角线 AC，BD 相交于点 O，过点 O 的一条直线分别交 AD，BC 于点 E，F．求证：AE=CF．

查看试题解析
22. 关于 $x$ 的一元二次方程 $x^{2} + 2 x + k - 4 = 0$ 有实数根．

(1)、求k的取值范围；

(2)、写出一个满足条件的 $k$ 的值，求此时方程的根．

查看试题解析
23. 下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程．
已知：四边形 $A B C D$ 是平行四边形．

求作：菱形 $A B E F$ （点 $E$ 在 $B C$ 上，点 $F$ 在 $A D$ 上）．

作法：①以 $A$ 为圆心， $A B$ 长为半径作弧，交 $A D$ 于点 $F$ ；

②以 $B$ 为圆心， $A B$ 长为半径作弧，交 $B C$ 于点 $E$ ；

③连接 $E F$ ．

所以四边形 $A B E F$ 为所求的菱形．

根据小明设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；

（保留作图痕迹）

(2)、完成下面的证明．
证明： $∵ A F = A B$ ， $B E = A B$ ，

$∴$ $=$ ．

在 $▱ A B C D$ 中， $A D ∥ B C$ ，

即 $A F ∥ B E$ ．

$∴$ 四边形 $A B E F$ 为平行四边形．（）（填推理的依据）

$∵ A F = A B$ ，

$∴$ 四边形 $A B E F$ 为菱形．（）（填推理的依据）

查看试题解析

24. 某校为了调査学生对垃圾分类知识的了解情况，从七、八两个年级各随机抽取40名学生进行了相关知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行了整理、描述和分析．下面给出了部分信息．

$a$ ．七年级40名学生成绩的频数分布统计表如下．

成绩 $x$	$50 \leq x < 60$	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x ⩽ 100$
学生人数	3	12	13	11	1

$b$ ．七年级成绩在 $70 \leq x < 80$ 这一组的是：

70 71 71 72 73 74 74 75 76 77 78 79 79

$c$ ．七、八两个年级成绩的平均分、中位数、众数和方差如下．

根据以上信息，回答下列问题：

年级	平均分	中位数	众数	方差
七	73.8	$n$	88	127
八	73.8	75	84	99.4

(1)、写出表中n的值；

(2)、在此次测试中，某学生的成绩是74分，在他所属年级排在前20名，由表中数据可知该学生是年级的学生．（填“七”或“八”）

(3)、根据以上信息，你认为七、八两个年级中，哪个年级学生了解垃圾分类知识的情况较好，请说明理由．

查看试题解析

25. 如图，小华要为一个长3分米，宽2分米的长方形防疫科普电子小报四周添加一个边框，要求边框的四条边宽度相等，且边框面积与电子小报内容所占面积相等，小华添加的边框的宽度应是多少分米？

查看试题解析

26. 有这样一个问题：探究函数

y = | x + 1 |

的图象与性质．

小强根据学习函数的经验，对函数 $y = | x + 1 |$ 的图象与性质进行了探究．下面是小强的探究过程，请补充完整：

(1)、在函数

y = | x + 1 |

中，自变量

x

的取值范围是；

(2)、下表是

y

与

x

的几组对应值．

$x$	$\dots$	-4	-3	-2	-1	0	1	2	3	$\dots$
$y$	$\dots$	3	2	1	0	1	$m$	3	4	$\dots$

①求m的值；

②如图，在平面直角坐标系 $x O y$ 中，描出补全后的表中各组对应值所对应的点，并画出该函数的图象；

(3)、结合函数图象，写出该函数的一条性质：．

查看试题解析

27. 在平面直角坐标系 $x O y$ 中，直线 $y = a x + b (a > 0)$ 经过点 $A (2 ， 2)$ 且交 $x$ 轴于点 $B$ ，过点 $A$ 作 $A C ⊥ x$ 轴于点 $C$ ．线段 $A B$ ， $A C$ ， $B C$ 围成的区域（不含边界）为 $W$ ．我们把横、纵坐标都是整数的点叫做整点．

(1)、若直线 $A B$ 与直线 $y = \frac{1}{2} x$ 平行．
①求点 $B$ 的坐标；

②直接写出区域 $W$ 内的整点个数；

(2)、若区域 $W$ 内没有整点，结合函数图象，直接写出 $a$ 的取值范围．

查看试题解析
28. 数学课上，李老师提出问题：如图 $1$ ，在正方形 $A B C D$ 中，点 $E$ 是边 $B C$ 的中点， $∠ A E F = 90 °$ ，且交 $E F$ 正方形外角的平分线 $C F$ 于点 $F$ ．求证： $A E = E F$ ．

经过思考，小聪展示了一种正确的解题思路．取 $A B$ 的中点 $H$ ，连接 $H E$ ，则 $△ B H E$ 为等腰直角三角形，这时只需证 $△ A H E$ 与 $△ E C F$ 全等即可．在此基础上，同学们进行了进一步的探究：

(1)、小颖提出：如图2，如果把“点 $E$ 是边 $B C$ 的中点”改为“点 $E$ 是边 $B C$ 上（不含点 $B$ ， $C$ ）的任意一点”，其他条件不变，那么结论“ $A E = E F$ ”仍然成立，你认为小颖的观点符合题意吗？如果符合题意，写出证明过程，如果错误，请说明理由；

(2)、小华提出：如图 $3$ ，如果点 $E$ 是边 $B C$ 延长线上的任意一点，其他条件不变，那么结论“ $A E = E F$ ”是否成立？（填“是”或“否”）；

(3)、小丽提出：如图4，在平面直角坐标系 $x O y$ 中，点 $O$ 与点 $B$ 重合，正方形的边长为 $1$ ，当 $E$ 为 $B C$ 边上（不含点 $B$ ， $C$ ）的某一点时，点 $F$ 恰好落在直线 $y = - 2 x + 3$ 上，请直接写出此时点 $E$ 的坐标．

查看试题解析

男衬衫号码	39号	40号	41号	42号	43号
销售数量/件	3	12	21	9	5

所挂物体质量 $x (kg)$	1	2	3	4	5
弹簧长度 $y (cm)$	10	12	14	16	18