湖北省十堰市房县2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、选择题

1. $- \sqrt{2}$ 的绝对值是（）

A、 $- \frac{\sqrt{2}}{2}$ B、 $\sqrt{2}$ C、 $- \sqrt{2}$ D、﹣2

查看试题解析
2. 如图，经过刨平的木板上的 $A ， B$ 两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）

A、点动成线； B、两点确定一条直线； C、垂线段最短； D、两点之间，线段最短；

查看试题解析
3. 在课堂上，老师在黑板上画出了如图所示的3个三角形，让同学们根据它们的边长进行分类，其中搭配错误的是（）

A、①——不等边三角形 B、②③——等腰三角形 C、③——等边三角形 D、②③——等边三角形

查看试题解析
4. 下列说法正确的是（）.

A、5是不等式5＋x＞10的一个解 B、x＜5是不等式x－5＞0的解集 C、x≥5是不等式－x≤－5的解集 D、x＞3是不等式x－3≥0的解集

查看试题解析
5. $a$ ， $b$ ， $c$ 是同一平面内的三条直线，下列说法错误的是（）

A、如果 $a ∥ b$ ， $b ∥ c$ ，那么 $a ∥ c$ B、如果 $a ∥ b$ ， $b ⊥ c$ ，那么 $a ⊥ c$ C、如果 $a ⊥ c$ ， $b ⊥ c$ ，那么 $a ⊥ c$ D、如果 $a ⊥ b$ ， $b ⊥ c$ ，那么 $a ∥ c$

查看试题解析
6. 中考结束后，小明想了解今年杭州各普高的录取分数线，他需要通过什么方法获得这些数据？（）

A、测量 B、查阅文献资料、互联网 C、调查 D、直接观察

查看试题解析
7. 一组同学参加植树活动，如果每人种5棵，还剩下3棵树苗；如果每人种6棵，缺少5棵树苗. 设共有 $x$ 名学生，树苗共有 $y$ 棵. 根据题意可列方程组（）

A、 ${\begin{matrix} 5 x = y + 3 \\ 6 x = y - 5 \end{matrix}$ B、 ${\begin{matrix} 5 x = y + 3 \\ 6 x = y + 5 \end{matrix}$ C、 ${\begin{matrix} 5 x = y - 3 \\ 6 x = y - 5 \end{matrix}$ D、 ${\begin{matrix} 5 x = y - 3 \\ 6 x = y + 5 \end{matrix}$

查看试题解析
8. 已知三角形的两边长分别为3 cm和4 cm，则该三角形第三边的长不可能是（）

A、1 cm B、3 cm C、5 cm D、6 cm

查看试题解析
9. 观察下列各式：3¹=3，3²=9，3³=27，3⁴=81，3⁵=243，3⁶=729，…则：3²⁰²⁰的个位数字是（）

A、3 B、9 C、7 D、1

查看试题解析
10. 已知点O(0,0),B(1,2),点A在坐标轴上,且S△_OAB=2,则满足条件的点A的个数（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 已知 ${\begin{array}{l} x = 1 \\ y = - 3 \end{array}$ 是方程3x﹣my＝1的一个解，则m＝

查看试题解析
12. 光明中学七年级甲、乙、丙三个班中，每班的学生人数都为 $40$ 名，某次数学考试的成绩统计如下：（如图，每组分数含最小值，不含最大值）根据图、表提供的信息，则 $80 ~ 90$ 分这一组人数最多的班是.

丙班数学成绩频数统计表

分数

$50 ~ 60$

$60 ~ 70$

$70 ~ 80$

$80 ~ 90$

$90 ~ 100$

人数

1

4

15

11

9

查看试题解析
13.
如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1+∠2=度．

查看试题解析
14. 对于任意实数a、b，定义一种运算：a※b=ab﹣a+b﹣2．例如，2※5=2×5﹣2+5﹣2=ll．请根据上述的定义解决问题：若不等式3※x＜2，则不等式的正整数解是．

查看试题解析
15. 如图，两个全等的直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB＝8， DH＝2，平移距离为3，则阴影部分的面积是.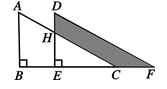

查看试题解析
16. 平面直角坐标系中，点A（－3，2），B（3，4），C（x，y），若AC//x轴，则线段BC的长度最小时点C的坐标为.

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{- 1} - \frac{5}{7} \times | - \sqrt{\frac{49}{25}} | + \sqrt{4}$

查看试题解析
18. 解不等式组： ${\begin{array}{l} x - 3 (x - 2) \geq 4 \\ \frac{1 - 2 x}{4} < 1 - x \end{array}$ ，并在数轴上表示其解集.

查看试题解析
19. 如图，是小明所在学校的平面示意图，已知宿舍楼的位置是（3，4），艺术楼的位置是（﹣3，1）.

（ 1 ）根据题意，画出相应的平面直角坐标系；

（ 2 ）分别写出教学楼、体育馆的位置；

（ 3 ）若学校行政楼的位置是（﹣1，﹣1），在图中标出行政楼的位置.

查看试题解析

20. 中华文明，源远流长；中华汉字，寓意深广．为了传承优秀传统文化，某校团委组织了一次全校1000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了200名学生的成绩（成绩

x

取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：

成绩 $x$ /分	频数	频率
$50 \leq x < 60$	10	0.05
$60 \leq x < 70$	20	0.10
$70 \leq x < 80$	30	$b$
$80 \leq x < 90$	$a$	0.30
$90 \leq x \leq 100$	80	0.40

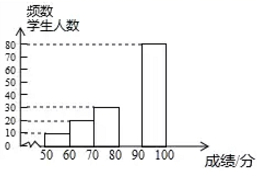
请根据所给的信息，解答下列问题：

(1)、

a =

，

b =

；

(2)、请补全频数分布直方图；

(3)、这次比赛成绩的中位数会落在分数段；

(4)、若成绩在90分以上（包括90分）的为优等，则该校参加这次比赛的1000名学生中成绩优等的大约有多少人？

查看试题解析

21. 小红和小凤两人在解关于x、y的方程组 ${\begin{array}{l} a x + 3 y = 5 ， \\ b x + 2 y = 8 . \end{array}$ 时，小红只因看错了系数a，得到方程组的解为 ${\begin{array}{l} x = - 1 ， \\ y = 2 . \end{array}$ ；小凤只因看错了系数b，得到方程组的解为 ${\begin{array}{l} x = 1 ， \\ y = 4 . \end{array}$ ；求a、b的值和原方程组的解.

查看试题解析
22. 如图，已知∠1＝∠2，DE⊥BC，AB⊥BC，求证：∠A＝∠3.

证明：∵ DE⊥BC，AB⊥BC(已知)

∴∠DEC=∠ABC=90°( ▲ )

∴DE∥AB（_▲）

∴∠2=_▲_ (_▲_)

∠1＝ ▲ (_▲_)

又∵∠1＝∠2(_▲_)

∴∠A＝∠3(_▲_)

查看试题解析
23. 我校组织一批学生开展社会实践活动，原计划租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出一辆车，且其余客车恰好坐满.已知45座客车租金为每辆220元，60座客车租金为每辆300元.

(1)、这批学生的人数是多少？原计划租用45座客车多少辆？

(2)、若租用同一种客车，要使每位学生都有座位，应该怎样租用合算？

查看试题解析
24. 如图，△ABC的顶点都在方格纸的格点上，将△ABC向右平移4格，再向上平移2格，其中每个格子的边长为1个单位长度.

(1)、在图中画出平移后的△A′B′C′；

(2)、若连接AA′、CC′，则这两条线段的关系是；

(3)、作△ABC的高AD，作△ABC的中线BE，作△ABC的角平分线CF.

查看试题解析
25. 在平面直角坐标系中， $O$ 为坐标原点.

(1)、已知点 $P (a - 1, 3 a + 6)$ 在 $y$ 轴上，求点 $P$ 的坐标.

(2)、已知两点 $A (- 3, m), B (n, 4)$ ，若 $A B / / x$ 轴，点 $B$ 在第一象限，求 $m$ 的值，并确定 $n$ 的取值范围.

(3)、在（1）（2）的条件下，如果线段 $A B$ 的长度是5，求以 $P, O, B$ 为顶点的三角形的面积.

查看试题解析

分数	$50 ~ 60$	$60 ~ 70$	$70 ~ 80$	$80 ~ 90$	$90 ~ 100$
人数	1	4	15	11	9