北京市大兴区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 为了加强生活垃圾管理,改善城乡环境,保障人体健康,2020年5月1日起,北京市实施《北京市生活垃圾管理条例》.下图分别是厨余垃圾,可回收物,有害垃圾,和其他垃圾的标识,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
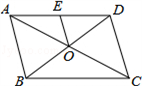
D、 2. 在平面直角坐标系中,点P(2, 1)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 关于x的一元二次方程 (m为常数)有实数根,则m的取值范围是( )A、 B、 C、 ≤ 0 D、 ≥04. 若正比例函数 的图象经过点(2,-1),则这个正比例函数的表达式为( )A、 B、 C、 D、5. 正多边形的一个外角的度数为72°,则这个正多边形的边数为( )A、4 B、5 C、6 D、76. 如图,在 中, 相交于点 .下列结论:① ,② ,③ ,④ ,⑤ .正确结论的个数是( )
2. 在平面直角坐标系中,点P(2, 1)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 关于x的一元二次方程 (m为常数)有实数根,则m的取值范围是( )A、 B、 C、 ≤ 0 D、 ≥04. 若正比例函数 的图象经过点(2,-1),则这个正比例函数的表达式为( )A、 B、 C、 D、5. 正多边形的一个外角的度数为72°,则这个正多边形的边数为( )A、4 B、5 C、6 D、76. 如图,在 中, 相交于点 .下列结论:① ,② ,③ ,④ ,⑤ .正确结论的个数是( ) A、5个 B、4个 C、3个 D、2个7. 在一次函数y=kx+b中,已知 <0,则下列的图象示意图中,正确的是( )A、
A、5个 B、4个 C、3个 D、2个7. 在一次函数y=kx+b中,已知 <0,则下列的图象示意图中,正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知:如图,正方形ABCD中,AB=2,AC , BD相交于点O , E , F分别为边BC , CD上的动点(点E , F不与线段BC , CD的端点重合)且BE=CF , 连接OE , OF , EF . 在点E , F运动的过程中,有下列四个结论:
8. 已知:如图,正方形ABCD中,AB=2,AC , BD相交于点O , E , F分别为边BC , CD上的动点(点E , F不与线段BC , CD的端点重合)且BE=CF , 连接OE , OF , EF . 在点E , F运动的过程中,有下列四个结论:
①△OEF是等腰直角三角形;②△OEF面积的最小值是 ;③至少存在一个△ECF , 使得△ECF的周长是 ;④四边形OECF的面积是1.所有符合题意结论的序号是( )
A、①②③ B、③④ C、①②④ D、①②③④二、填空题
-
9. 函数y= 中,自变量x的取值范围是 .10. 点P(2,-3)关于x轴对称的点P′的坐标是 .11. 一元二次方程 的根12. 甲、乙两名同学在射击选拔比赛中,各射击10次,平均成绩都是是7.5环,方差分别是 ,则在本次测试中,成绩更稳定的同学是(填“甲”或“乙”).13. 若一个一次函数图象经过第一、二、三象限,且经过点(0,4),写出一个满足条件的一次函数表达式 .14. 如图,▱ABCD的对角线AC、BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是.
 15. 二次三项式 的最小值是 .16. 在平面直角坐标系中,点P是直线 上的动点,过点P作直线l垂直于x轴,直线l与直线 相交于点Q , 设点P的横坐标为m , 当PQ >6时,m的取值范围是 .
15. 二次三项式 的最小值是 .16. 在平面直角坐标系中,点P是直线 上的动点,过点P作直线l垂直于x轴,直线l与直线 相交于点Q , 设点P的横坐标为m , 当PQ >6时,m的取值范围是 .三、解答题
-
17. 已知一次函数的图象经过点(-3,5) 和(5,9),求这个一次函数的表达式.18. 解方程: .19. 某学校初二年级进行“垃圾分类,从我做起”垃圾分类知识竞赛活动,并对测试成绩进行了分组整理,各分数段的人数如图所示(满分100分).
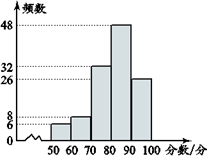
请观察统计图,填空并回答下列问题:
(1)、这个学校初二年级共有名学生;(2)、成绩在分数段的人数最多、最集中,占全年级总人数的比值是 ;(3)、若从该年级随意找出一名学生,他的测试成绩在分数段的可能性最小,可能性是 .20. 若m是方程x2+x-1=0的一个根,求代数式m3+2m2+2019的值.21. 已知关于x的一元二次方程 有两个不相等的实数根,求m的取值范围.22. 如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.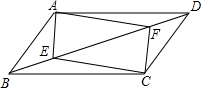 23. 如图,有一面积为150平方米的矩形花圃,花圃的一边靠墙(墙长18米),另三边用竹篱笆围成.如果竹篱笆的长为35米,求矩形花圃的长和宽各是多少米?
23. 如图,有一面积为150平方米的矩形花圃,花圃的一边靠墙(墙长18米),另三边用竹篱笆围成.如果竹篱笆的长为35米,求矩形花圃的长和宽各是多少米? 24. 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,求∠BAE的度数.
24. 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,求∠BAE的度数.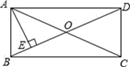 25. 如图,已知△ABC , D是AC的中点,DE⊥AC于点D , 交AB于点E , 过点C作CF∥BA交ED的延长线于点F , 连接CE , AF . 求证:四边形AECF是菱形.
25. 如图,已知△ABC , D是AC的中点,DE⊥AC于点D , 交AB于点E , 过点C作CF∥BA交ED的延长线于点F , 连接CE , AF . 求证:四边形AECF是菱形. 26. 如图,直线 与直线 相交于点M(1,m).
26. 如图,直线 与直线 相交于点M(1,m). (1)、求m , n的值;(2)、结合函数图象,直接写出不等式 的解集;(3)、求两条直线与x轴围成的三角形面积.27. 为鼓励居民节约用水,某市自来水公司采取分段收费标准,下图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
(1)、求m , n的值;(2)、结合函数图象,直接写出不等式 的解集;(3)、求两条直线与x轴围成的三角形面积.27. 为鼓励居民节约用水,某市自来水公司采取分段收费标准,下图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系. (1)、当月用水量 时,收费标准是元/吨;(2)、小华家五月份用水16吨,应交水费多少元?(3)、按上述分段收费标准,某居民家三、四月份分别交水费81元和56元,问四月份比三月份节约用水多少吨?28. 已知: 是等边三角形,点D在射线BC上,连接AD , 将线段AD绕点A逆时针旋转 得到线段 AE , 连接EC , 作EF // BC交直线AB于点F .
(1)、当月用水量 时,收费标准是元/吨;(2)、小华家五月份用水16吨,应交水费多少元?(3)、按上述分段收费标准,某居民家三、四月份分别交水费81元和56元,问四月份比三月份节约用水多少吨?28. 已知: 是等边三角形,点D在射线BC上,连接AD , 将线段AD绕点A逆时针旋转 得到线段 AE , 连接EC , 作EF // BC交直线AB于点F .
 (1)、当点D在线段BC上时,如图1,
(1)、当点D在线段BC上时,如图1,①依据题意,补全图1;
②猜想线段AB , AF , BD的数量关系,并证明;
(2)、当点D在线段BC的延长线上时,直接写出线段AB , AF , BD的数量关系.