湖北省十堰市房县2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、选择题

1. 1﹣ $\sqrt{2}$ 的相反数是（）

A、 1﹣ $\sqrt{2}$ B、 $\sqrt{2}$ ﹣1 C、 $\sqrt{2}$ D、﹣1

查看试题解析
2. 我国数学家华罗庚曾建议，用一副反应勾股定理的数形关系图来作为和外星人交谈的语言，就勾股定理本身而言，它揭示了直角三角形的三边之间的关系，它体现的数学思想方法是（）

A、分类思想 B、方程思想 C、转化 D、数形结合

查看试题解析
3. 下列图案中，含有旋转变换的有（） .

A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 下列计算错误的是（）

A、 $\sqrt{8}$ ﹣ $\sqrt{2}$ ＝ $\sqrt{2}$ B、 $\sqrt{8}$ ÷2＝ $\sqrt{2}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、3+2 $\sqrt{2}$ =5 $\sqrt{2}$

查看试题解析
5. 下列说法中错误的是（）

A、四边相等的四边形是菱形 B、对角线相等的矩形是正方形 C、一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是菱形

查看试题解析
6. 有一组数据：2，5，5，6，7，每个数据加1后的平均数为（）

A、3 B、4 C、5 D、6

查看试题解析
7. 现代互联网技术的广泛应用，促进快递行业高速发展，据调查，某家快递公司，今年5月份与7月份完成投递的快递总件数分别为8.5万件和10万件，设该快递公司这两个月投递总件数的月平均增长率为x，则下列方程正确的是（）

A、8.5（1+2x）=10 B、8.5（1+x）=10 C、8.5（1+x）²=10 D、8.5+8.5（1+x）+8.5（1+x）²=10

查看试题解析
8. 如图1，园丁住宅小区有一块草坪如图所示.已知AB=3米，BC=4米，CD=12米，DA=13米，且AB⊥BC，这块草坪的面积是（）

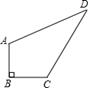A、24米² B、36米² C、48米² D、72米²

查看试题解析
9. 将全体正奇数排成一个三角形数阵：

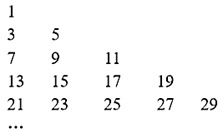
按照以上排列的规律，第25行第19个数是（）

A、639 B、637 C、635 D、633

查看试题解析
10. 已知直线y＝(3m+2)x＋2和y＝－3x＋6交于x轴上同一点，m的值为（）

A、－2 B、2 C、－1 D、0

查看试题解析

二、填空题

11. 已知关于 $x$ 的一元二次方程 $(a - 3) x^{2} - 2 x + a^{2} - 9 = 0$ 的常数项是 $0$ ，则 $a =$ .

查看试题解析

12. 小张和小李练习射击，两人10次射击训练成绩（环数）的统计结果如表所示，

	平均数	中位数	众数	方差
小张	7.2	7.5	7	1.2
小李	7.1	7.5	8	5.4

通常新手的成绩不稳定，根据表格中的信息，估计小张和小李两人中新手是.

查看试题解析

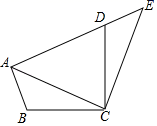
13. 如图，将△ABC绕点C顺时针旋转90°得到△EDC.若点A，D，E在同一条直线上，∠ACB＝20°，则∠ADC的度数是.

查看试题解析
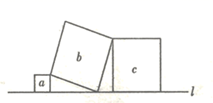
14. 对于能使式子有意义的有理数a，b，定义新运算：a△b＝ $\frac{3 a + b}{a - 3 b}$ .如果 $| \begin{array}{l} x + 1 \end{array} | + \sqrt{y - 3} + | x z + 2 | = 0$ ，则x△(y△z)= .

查看试题解析
15. 如图，直线l上有三个正方形a，b，c，若a，c的面积分别为1和9，则b的面积为.

查看试题解析
16. 如图，四边形ABCD中，AD∥BC，AC平分∠BAD，∠ABC=60°，E为AD上一点，AE=2，DE=4，P为AC 上一点，则△PDE周长的最小值为.

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{- 1} - (\sqrt[3]{8} - 4) \div \sqrt{{(- 2)}^{2}}$

查看试题解析
18. 解方程： $x^{2} + 4 x - 12 = 0$

查看试题解析
19. 如图，某地方政府决定在相距50km的A、B两站之间的公路旁E点，修建一个土特产加工基地，且使C、D两村到E点的距离相等，已知DA⊥AB于A，CB⊥AB于B，DA=30km，CB=20km，那么基地E应建在离A站多少千米的地方？

查看试题解析

20. 某校初三进行了第三次模拟考试，该校领导为了了解学生的数学考试情况，抽样调查部分学生的数学成绩，并将抽样的数据进行了如下整理：

①如下分数段整理样本；

等级等级	分数段	各组总分	人数
A	110＜X≤120	P	4
B	100＜X≤110	843	n
C	90＜X≤100	574	m
D	80＜X≤90	171	2

②根据左表绘制扇形统计图.

(1)、填空m＝， n＝，数学成绩的中位数所在的等级；

(2)、如果该校有1200名学生参加了本次模拟测，估计D等级的人数；

(3)、已知抽样调查学生的数学成绩平均分为102分，求A等级学生的数学成绩的平均分数.

查看试题解析

21. 关于的一元二次方程x²+2x+k+1=0的实数解是x₁和x₂ ．

(1)、求k的取值范围；

(2)、如果x₁+x₂﹣x₁x₂＜﹣1且k为整数，求k的值．

查看试题解析
22. 如图，在矩形ABCD中，直线l经过对角线AC的中点O(直线l不与线段AC重合)，与AB、CD交于点E、F.

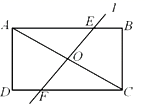(1)、求证：BE = DF；

(2)、当直线l⊥AC时，若AD = 4，AB = 6，求CF的长.

查看试题解析
23. 某饮料厂生产一种饮料，经测算，用1吨水生产的饮料所获利润y（元）是1吨水的价格x（元）的一次函数.

(1)、根据下表提供的数据，求y与x的函数关系式；当水价为每吨10元时，1吨水生产出的饮料所获的利润是多少？

1吨水价格x（元）

4

6

用1吨水生产的饮料所获利润y（元）

200

198

(2)、为节约用水，这个市规定：该厂日用水量不超过20吨时，水价为每吨4元；日用水量超过20吨时，超过部分按每吨40元收费.已知该厂日用水量不少于20吨，设该厂日用水量为t吨，当日所获利润为W元.求W与t的函数关系式；

(3)、该厂加强管理，积极节水，使日用水量不超过25吨，但仍不少于20吨，求该厂的日利润的取值范围.

查看试题解析
24. 如图(1)，已知△ABC是等腰直角三角形，∠BAC＝90°，点D是BC的中点.作正方形DEFG，使点A、C分别在DG和DE上，连接AE、BG.

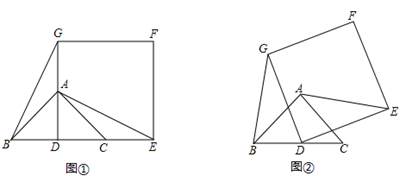(1)、试猜想线段BG和AE的关系(位置关系及数量关系)，请直接写出你得到的结论；

(2)、将正方形DEFG绕点D逆时针方向旋转一角度α后(0°＜α＜90°)，如图(2)，通过观察或测量等方法判断(1)中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由；

(3)、若BC＝DE＝2，正方形DEFG绕点D逆时针方向旋转角度α (0°＜α＜360°)过程中，当BG为最小值时，求AF的值.

查看试题解析
25. 如图1，直线l：y＝ $\frac{1}{2}$ x+2与x轴交于点A，与y轴交于点B．已知点C（﹣2，0）．

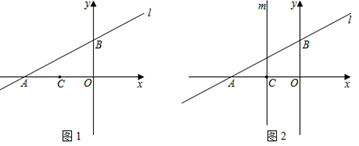(1)、求出点A，点B的坐标．

(2)、P是直线AB上一动点，且△BOP和△COP的面积相等，求点P坐标．

(3)、如图2，平移直线l，分别交x轴，y轴于交于点A₁ ， B₁ ，过点C作平行于y轴的直线m，在直线m上是否存在点Q，使得△A₁B₁Q是等腰直角三角形？若存在，请直接写出所有符合条件的点Q的坐标．

查看试题解析

1吨水价格x（元）	4	6
用1吨水生产的饮料所获利润y（元）	200	198