河南省信阳市罗山县2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、选择题

1. 下列式子中，属于最简二次根式的是

A、 $\sqrt{9}$ B、 $\sqrt{7}$ C、 $\sqrt{20}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 在直角坐标系中，点P(-2，3)到原点的距离是（）

A、 $\sqrt{5}$ B、 $\sqrt{13}$ C、 $\sqrt{11}$ D、2

查看试题解析
3. “倡导全民阅读”、“推动国民素质和社会文明程度显著提高”已成为新时期的重要工作.教育主管部门对某学校青年教师2019年度阅读情况进行了问卷调查，并将收集的数据统计如表，根据表中的信息判断，下列结论错误的是（）

A、该学校中青年教师2019年度看书数量的中位数为4本 B、该学校中青年教师2019年平均每人阅读8本书 C、该学校中参与调查的青年教师人数为40人 D、该学校中青年教师2019年度看书数量的众数为4本

查看试题解析
4. 有100名学生参加两次科技知识测试，条形图显示两次测试的分数分布情况如图所示：根据条形图提供的信息，下列说法中，正确的是（）

A、两次测试，最低分在第二次测试中 B、第一次测试和第二次测试的平均分相同 C、第一次分数的中位数在20～39分数段 D、第二次分数的中位数在60～79分数段

查看试题解析
5. 小明的作业本上做了以下四题：
① $\sqrt{16 a^{4}} = 4 a^{2}$ ② $\sqrt{5 a} \cdot \sqrt{10 a} = 5 \sqrt{2} a$ ③ $a \sqrt{\frac{1}{a}} = \sqrt{a^{2} \cdot \frac{1}{a}} = \sqrt{a}$ ④ $\sqrt{3 a} - \sqrt{2 a} = \sqrt{a}$

其中做错的题是（）

A、① B、② C、③ D、④

查看试题解析
6. 已知四边形ABCD中，AC与BD交于点O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下四种说法：
①如果再加上条件“BC＝AD”，那么四边形ABCD一定是平行四边形；②如果再加上条件“∠BAD＝∠BCD”，那么四边形ABCD一定是平行四边形；③如果再加上条件“OA＝OC”，那么四边形ABCD一定是平行四边形；④如果再加上条件“∠DBA＝∠CAB”，那么四边形ABCD一定是平行四边形.其中正确的说法是（）

A、①② B、①③④ C、②③ D、②③④

查看试题解析
7. 已知a、b、c是三角形的三边长，如果满足 ${(a - 6)}^{2} + \sqrt{b - 8} + | c - 10 |$ =0，则三角形的形状是（）

A、底与边不相等的等腰三角形 B、等边三角形 C、钝角三角形 D、直角三角形

查看试题解析
8. 如图所示，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2m，梯子的顶端B到地面距离为7m，现将梯子的底端A向外移到A'，使梯子的底端A'到墙根O距离为3m，同时梯子顶端B下降至B'，那么BB' （）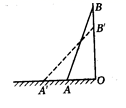

A、等于1m B、小于1m C、大于1m D、以上都不对

查看试题解析
9. 八个边长为1的正方形如图摆放在平面直角坐标系中，经过P点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（）

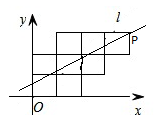A、 $y = \frac{5}{8} x + \frac{1}{2}$ B、 $y = \frac{7}{8} x + \frac{1}{2}$ C、 $y = \frac{7}{6} x + \frac{1}{2}$ D、 $y = \frac{3}{4} x + \frac{1}{2}$

查看试题解析
10. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示.则下列结论：①A，B两城相距300千米；②乙车比甲车晚出发1小时，却早到1.5小时；③乙车出发后2.5小时追上甲车；④当甲、乙两车相距40千米时，t＝ $\frac{3}{2}$ 或t＝ $\frac{7}{2}$ ，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 在函数y= $\frac{1 - x}{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
12. 某校规定学生的学期学业成绩由三部分组成：平时占20%，期中占30%，期末占50%，小颖的平时、期中、期末成绩分别为85分、90分、92分，则她本学期的学业成绩为分.

查看试题解析
13. 如图，点O是矩形ABCD的对角线AC的中点，OM∥AB交AD于点M，若OM=2，BC=6，则OB的长为.

查看试题解析
14. 如图，一次函数y=﹣x+1与y=2x+m的图象相交于点P(n，2)，则关于x的不等式﹣x+1 ≥ 2x+m的解集为.

查看试题解析
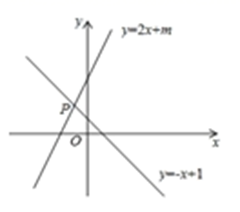15. 如图，正方形ABCD的边长是18，点E是AB边上的一个动点，点F是CD边上一点， $C F = 8$ ，连接EF，把正方形ABCD沿EF折叠，使点A，D分别落在点 $A^{'}$ ， $D^{'}$ 处，当点 $D^{'}$ 落在直线BC上时，线段AE的长为.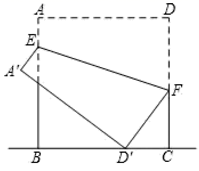

查看试题解析

三、解答题

16. 计算.

(1)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$ ；

(2)、 $(\sqrt{12} + \sqrt{3}) \times \sqrt{6} - 2 \sqrt{\frac{1}{2}}$ .

查看试题解析
17. 某校举办了一次知识竞赛，满分10分，学生得分均为整数，成绩达到6分以上（包括6分）为合格，达到9分以上（包括9分）为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示.

(1)、补充完成下面的成绩统计分析表：

(2)、小明同学说：“这次竞赛我得了7分，在我们小组中排名属中游偏上!”观察上表可知，小明是组的学生；（填“甲”或“乙”）

(3)、甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组，请你给出两条支持乙组同学观点的理由.

查看试题解析
18. 先阅读下面的解题过程，然后再解答.形如 $\sqrt{m \pm 2 \sqrt{n}}$ 的化简，我们只要找到两个数a，b，使 $a + b = m$ ， $a b = n$ ，即 ${(\sqrt{a})}^{2} + {(\sqrt{b})}^{2} = m$ ， $\sqrt{a} \cdot \sqrt{b} = \sqrt{n}$ ，那么便有： $\sqrt{m \pm 2 \sqrt{n}} = \sqrt{{(\sqrt{a} \pm \sqrt{b})}^{2}} = \sqrt{a} \pm \sqrt{b} (a > b ⩾ 0)$ .
例如化简： $\sqrt{7 + 4 \sqrt{3}}$ .

解：首先把 $\sqrt{7 + 4 \sqrt{3}}$ 化为 $\sqrt{7 + 2 \sqrt{12}}$ ，

这里 $m = 7$ ， $n = 12$ ，

由于 $4 + 3 = 7$ ， $4 \times 3 = 12$ ，

所以 ${(\sqrt{4})}^{2} + {(\sqrt{3})}^{2} = 7, \sqrt{4} \times \sqrt{3} = \sqrt{12}$ ，

所以 $\sqrt{7 + 4 \sqrt{3}} = \sqrt{7 + 2 \sqrt{12}} = \sqrt{{(\sqrt{4} + \sqrt{3})}^{2}} = 2 + \sqrt{3}$ .

根据上述方法化简： $\sqrt{13 - 2 \sqrt{42}}$ .

查看试题解析
19. 如图在平静的湖面上，有一支红莲BA，高出水面的部分AC为1米，一阵风吹来，红莲被吹到一边，花朵齐及水面(即AB=DB)，已知红莲移动的水平距离CD为3米，则湖水深CB为多少？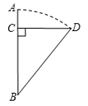

查看试题解析
20. 如图，▱ABCD中，G是CD的中点，E是边长AD上的动点，EG的延长线与BC的延长线相交于点F，连接CE，DF.

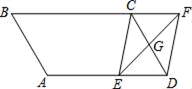(1)、求证：四边形CEDF是平行四边形.

(2)、填空：若AB＝3cm，BC＝5cm，∠B＝60°，则①当AE＝时，四边形CEDF是矩形；②当AE＝时，四边形CEDF是菱形.

查看试题解析
21. 如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 $y$ （千瓦时）关于已行驶路程 $x$ （千米）的函数图象.

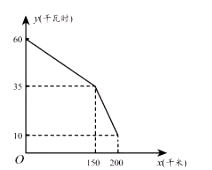(1)、根据图象，直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程，当 $0 \leq x \leq 150$ 时，求1千瓦时的电量汽车能行驶的路程；

(2)、当 $150 \leq x \leq 200$ 时求 $y$ 关于 $x$ 的函数表达式，并计算当汽车已行驶180千米时，蓄电池的剩余电量.

查看试题解析
22. 如图，直线y=kx+b经过点A（-5，0），B（-1，4）

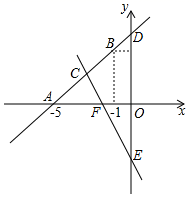(1)、求直线AB的表达式；

(2)、求直线CE：y=-2x-4与直线AB及y轴围成图形的面积；

(3)、根据图象，直接写出关于x的不等式kx+b＞-2x-4的解集.

查看试题解析
23. 如图1，我们把对角线互相垂直的四边形叫做垂美四边形.

(1)、概念理解：我们已经学习了平行四边形、菱形、矩形、正方形，在这四种图形中是垂美四边形的是.

(2)、性质探究：如图2，已知四边形ABCD是垂美四边形，试探究其两组对边AB，CD与BC，AD之间的数量关系，并写出证明过程.

(3)、问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，CE交AB于点M，已知AC=4，AB=5，求GE的长.

查看试题解析