河南省三门峡市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-14 类型:期末考试
一、选择题
-
1. 以下列各组数为边长,能构成直角三角形的是( )A、1,2,3 B、2,3,4 C、2,2,3 D、1,2,2. 下列二次根式中属于最简二次根式的是( )A、 B、 C、 D、3. 如图所示,在数轴上点A所表示的数为 ,则 的值为( )
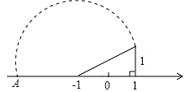 A、 B、 C、 D、4. 下列各式计算正确的是( )A、 B、 C、 D、5. 星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
A、 B、 C、 D、4. 下列各式计算正确的是( )A、 B、 C、 D、5. 星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )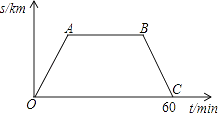 A、
A、 B、
B、 C、
C、 D、
D、 6. 甲,乙,丙,丁四人进行射击测试,每人测试10次,平均成绩均为9.2环,方差如下表所示:
6. 甲,乙,丙,丁四人进行射击测试,每人测试10次,平均成绩均为9.2环,方差如下表所示:选手
甲
乙
丙
丁
方差
0.50
0.56
0.45
0.60
则在这四个选手中,成绩最稳定的是( )
A、甲 B、乙 C、丙 D、丁7. 若点A(- ,m),B(- ,n)在一次函数y=-2x+3图象上,则m与n的大小关系是( )A、 B、 C、 D、无法确定8. 如图,菱形ABCD中,点E,F分别是AC,DC的中点.若EF=5,则菱形ABCD的周长为( ) A、15 B、20 C、30 D、409. 如图,菱形 的一边 在 轴上,将菱形 绕原点 顺时针旋转60°至 的位置,若点 与点 重合, , ,则点 的坐标为( )
A、15 B、20 C、30 D、409. 如图,菱形 的一边 在 轴上,将菱形 绕原点 顺时针旋转60°至 的位置,若点 与点 重合, , ,则点 的坐标为( )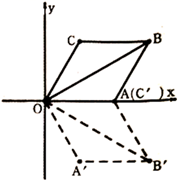 A、 B、 C、 D、10. 正方形 , , ,…,按如图所示的方式放置.点 , , ,…和点 , , ,…,分别在直线 和 轴上,已知点 , ,则 的坐标是( )
A、 B、 C、 D、10. 正方形 , , ,…,按如图所示的方式放置.点 , , ,…和点 , , ,…,分别在直线 和 轴上,已知点 , ,则 的坐标是( )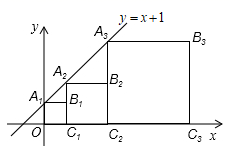 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 式子 在实数范围内有意义,则x的取值范围是.12. 如果数据3,4,x,5的平均数是4,那么该组数据的众数是.13. 直角三角形的三边长分别为 、 、 ,若 , ,则 .14. 如图,直线 与直线 交于点 ,则关于 的不等式 的解集是.
 15. 如图,矩形 中, ,点 在 上,且 ,连接 ,将 沿直线 翻折,点 恰好落在 上的点 处,则 .
15. 如图,矩形 中, ,点 在 上,且 ,连接 ,将 沿直线 翻折,点 恰好落在 上的点 处,则 .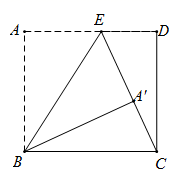
三、解答题
-
16. 计算:(1)、(2)、17. 已知a,b分别为等腰三角形的两条边长,且a,b满足b=4+ +3 ,求此三角形的周长.18. 如图,在 中, 是 边上的一点,已知 , , , .
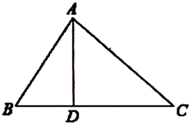 (1)、求证: ;(2)、求 的长.19. 某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
(1)、求证: ;(2)、求 的长.19. 某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:方式一:金卡售价600元/张,每次凭卡不再收费;
方式二:银卡售价150元/张,每次凭卡另收10元.
暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳 次时,所需总费用为 元.
 (1)、直接写出选择银卡、普通票消费时, 与 之间的函数关系式:
(1)、直接写出选择银卡、普通票消费时, 与 之间的函数关系式:银卡:;
普通卡:.
(2)、在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请求出点 , , 的坐标;(3)、根据函数图象回答,当游泳次数次时,选择普通卡更合算:当游泳次数次时,选择银卡更合算;当游泳次数次时,选择金卡更合算.20. 为提高中小学生的安全意识,三门峡市外国语高中举办“珍爱生命,预防溺水”知识竞赛活动.现从高一,高二两个年级各随机抽取20名参赛学生的成绩数据(百分制)进行调查分析,过程如下,请补充完整.收集数据:
高一年级:
76 88 93 65 78 94 89 68 95 70
89 78 89 89 77 94 87 88 92 91
高二年级:
74 97 91 89 98 74 69 87 72 78
99 72 97 86 99 74 99 73 98 74
整理、描述数据:
高一
2
7
6
高二
1
8
8
分析数据:
年级
平均数
中位数
众数
高一
84.5
88.5
高二
85
74
根据以上数据分析,回答下列问题:
(1)、 , ;(2)、 , ;(3)、请推断年级同学的竞赛成绩较好,理由为.21. 如下是小东设计的“作平行四边形一边中点”的尺规作图过程.已知:平行四边形 .
求作:点 ,使点 为边 的中点.
作法:如图,
①作射线 ;
②以点 为圆心, 长为半径画弧,
交 的延长线于点 ;
③连接 交 于点 .
所以点 就是所求作的点.
根据小东设计的尺规作图过程,
 (1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接 , .
四边形 是平行四边形,
.
▲ ,
四边形 是平行四边形 ▲ (填推理的依据).
▲ (填推理的依据).
点 为所求作的边 的中点.
22. 问题:探究函数 的图象与性质.小强根据学习函数的经验,对函数 的图象与性质进行了研究,下面是其研究过程,请补充完整.
(1)、自变量 的取值范围是全体实数, 与 的几组对应值列表如下:…
-4
-3
-2
-1
0
1
2
3
4
5
…
…
6
5
4
2
1
2
3
5
…
其中, , .
(2)、在如图所示的平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象;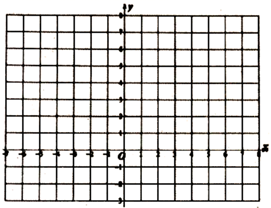 (3)、观察图象,写出该函数的两条性质.23. 在菱形 中, ,点 和点 分别是射线 和射线 上的点(不与 , 重合),且 .
(3)、观察图象,写出该函数的两条性质.23. 在菱形 中, ,点 和点 分别是射线 和射线 上的点(不与 , 重合),且 .
 (1)、问题初现
(1)、问题初现如图1,当点 和点 分别在线段 和线段 上(不与端点重合)时,线段 , , 之间的数量关系是;
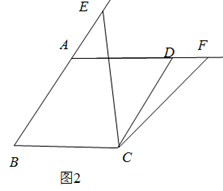
(2)、深入探究如图2,当点 和点 分别在线段 和线段 的延长线上(不与端点重合)时,线段 , , 之间有怎样的数量关系?请说明理由;
(3)、拓展应用在(2)的条件下,若 ,且 ,则 .