甘肃省兰州市教育局第四片区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若a＞b，则下列四个不等式中正确的是（）

A、3a＞3b B、a+5＜b+5 C、-5a＞-5b D、a-2＜b-2

查看试题解析
3. 下列式子：① $\frac{2}{x}$ ；② $\frac{x + y}{5}$ ；③ $\frac{1}{2 - a}$ ；④ $\frac{x}{π}$ ，其中是分式的有（）

A、①② B、①③④ C、①③ D、①②④

查看试题解析
4. 不等式 $5x - 1>2x + 5$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 已知实数x，y满足 $| x - 6 | + {(y - 7)}^{2} = 0$ ，则以x，y的值为两边的等腰三角形的周长为（）

A、19 B、20 C、19或20 D、以上答案都不对

查看试题解析
6. 平面直角坐标系中，点P（2，0）平移后对应的点为Q（5，4），则平移的距离为（）

A、3 B、4 C、5 D、7

查看试题解析
7. 下列分式的运算正确的是（）

A、 $\frac{1}{x} - \frac{1}{y} = \frac{1}{x y}$ B、 $\frac{x^{2} - 1}{{(x - 1)}^{2}} = \frac{x + 1}{x - 1}$ C、 $\frac{x - 2}{4 - x^{2}} = \frac{1}{x + 2}$ D、 $\frac{3}{x} \div \frac{x}{3} = 1$

查看试题解析
8. 在四边形ABCD中，下列说法正确的是（）

A、当AD=BC，AB∥DC时，四边形ABCD是平行四边形 B、当AD=BC，AB=DC时，四边形ABCD是平行四边形 C、当AC=BD，AC平分BD时，四边形ABCD是平行四边形 D、当AC=BD，AC⊥BD时，四边形ABCD是平行四边形

查看试题解析
9. 如图，在△ABC中，DE是边AB的垂直平分线，垂足为E，交BC边于D点，若AC＝5 cm，△ADC的周长为17 cm，则BC的长为（）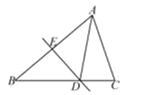

A、7 cm B、10 cm C、12 cm D、22 cm

查看试题解析
10. 如图，直线 $y = k_{1} x + b_{1}$ 与 $x$ 轴交于点(-4，0)，直线 $y = k_{2} x + b_{2}$ 与 $x$ 轴交于点(3，0)，则不等式组 ${\begin{array}{l} k_{1} x + b_{1} > 0 \\ k_{2} x + b_{2} > 0 \end{array}$ 的解集是（）

A、 $x > - 4$ B、 $x < 3$ C、 $- 4 < x < 3$ D、 $x < - 4 或 x > 3$

查看试题解析
11. 如图，在 $△ ABC$ 中， $AB = AC = 10$ ， $∠ BAC = 120^{\circ}$ ，AD是 $△ ABC$ 的中线，AE是 $∠ BAD$ 的角平分线， $DF / / AB$ 交AE的延长线于点F，则DF的长是 $($ $)$

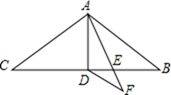A、2 B、4 C、5 D、 $\frac{5}{2}$

查看试题解析
12. 如图，平行四边形ABCD中，对角线AC、BD相交于点O，E、F是AC上的两点，当E、F满足下列哪个条件时，四边形DEBF不一定是平行四边形（）

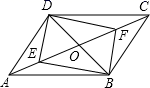A、∠ADE=∠CBF B、∠ABE=∠CDF C、DE=BF D、OE=OF

查看试题解析

二、填空题

13. 一个 $n$ 边形内角和为 $540^{\circ}$ ，则 $n$ 等于.

查看试题解析
14. 如图，在△ABC中，AB=BC，∠ABC= $100^{\circ}$ ，BD是∠ABC的平分线，E是AB的中点，则∠EDB的度数为.

查看试题解析
15. 若 $x^{2} + (m - 3) x + 4$ 是完全平方式，则数 $m$ 的值是.

查看试题解析
16. 若不等式组 ${\begin{array}{l} x < 3 \\ x > 2 m - 1 \end{array}$ 无解，则m的取值范围是.

查看试题解析

三、解答题

17. 因式分解：

(1)、 $2 x^{2} y - 8 x y + 8 y$

(2)、 ${(a + 2 b)}^{2} - {(2 a - b)}^{2}$

查看试题解析
18.

(1)、解不等式 $3 (x - 2) > 2 (7 - x)$ ，并把它的解集表示在数轴上.

(2)、 ${\begin{array}{l} 6 x + 2 \geq 3 x - 4 \\ \frac{2 x + 1}{3} - \frac{1 - x}{2} \leq 1 \end{array}$

查看试题解析
19. 解分式方程： $\frac{1}{x - 3} - \frac{8 x}{x^{2} - 9} = 1 + \frac{x}{3 - x}$

查看试题解析
20. 先化简，再求值： $(1 - \frac{1}{m + 2}) \div \frac{m^{2} + 2 m + 1}{2 m + 2}$ ，其中 $m = \sqrt{2} - 2$

查看试题解析
21. 如图，在平面直角坐标系中，已知 $Δ A B C$ 的三个顶点坐标分别是 $A (1 ， 1) ， B (4 ， 1) ， C (3 ， 3)$ .

( 1 )将 $Δ A B C$ 向下平移5个单位后得到 $Δ A_{1} B_{1} C_{1}$ ，请画出 $Δ A_{1} B_{1} C_{1}$ ；

( 2 )将 $Δ A B C$ 绕原点 $O$ 逆时针旋转90°后得到 $Δ A_{2} B_{2} C_{2}$ ，请画出 $Δ A_{2} B_{2} C_{2}$ ；

查看试题解析
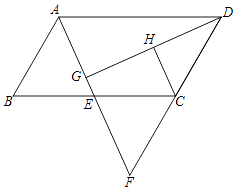
22. 如图，在四边形ABC中，AB=2cm，BC=4cm，CD=5cm，AD= $\sqrt{5}$ cm，∠A= $90^{\circ}$ ，求四边形ABCD的面积.

查看试题解析
23. 在数学课上，老师出了这样一道题：甲、乙两地相距1200 千米，乘高铁列车从甲地到乙地比乘特快列车少用8小时，已知高铁列车的平均行驶速度是特快列车的3倍，求特快列车从甲地到乙地的时间.

查看试题解析
24. 如图，▱ABCD的对角线AC、BD相交于点O，且E、F、G、H分别是AO、BO、CO、DO的中点.

(1)、求证：四边形EFGH是平行四边形；

(2)、若AC+BD=36，AB=10，求△OEF的周长.

查看试题解析
25. 如图，四边形ABCD为平行四边形，E为BC的中点，连接AE并延长交DC的延长线于点F．

(1)、求证：△ABE≌△FCE；

(2)、过点D作DG⊥AE于点G，H为DG的中点．判断CH与DG的位置关系，
并说明理由．

查看试题解析
26. 如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG.

(1)、求证：四边形DEFG是平行四边形；

(2)、若OB⊥OC，∠EOM和∠OCB互余，OM=4，求DG的长度.

查看试题解析