甘肃省天水市麦积区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-14 类型:期末考试
一、选择题
-
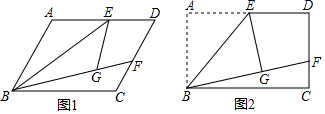
1. 点 在平面直角坐标系的( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 若分式 有意义,则实数 的取值范围是( )A、 B、 C、 D、3. 要判断甲、乙两队舞蹈队的身高哪队比较整齐,通常需要比较这两队舞蹈队身高的( )A、方差 B、中位数 C、众数 D、平均数4. 在平面直角坐标系中,点P(﹣3,2)关于x轴的对称点的坐标为( )A、(2,﹣3) B、(﹣2,3) C、(﹣3,2) D、(﹣3,﹣2)5. 测得某人一根头发的直径约为0.000 071 5米,该数用科学记数法可表示为( )A、0.715×104 B、0.715×10﹣4 C、7.15×105 D、7.15×10﹣56. 已知反比例函数 ,下列结论不正确的是( ).A、该函数图象经过点(-1,1) B、该函数图象在第二、四象限 C、当x<0时,y随x增大而减小 D、当x>1时,7. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )
 A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当AC=BD时,它是矩形 D、当∠ABC=90°时,它是正方形8. 某校八年级学生去距学校10km的科技馆参观,一部分学生骑自行车,过了30min,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑自行车学生速度的4倍,设骑自行车学生的速度为xkm/h,则下列方程正确的是( )A、 B、 C、 D、9. 已知四边形ABCD中,AB∥CD,对角线AC与BD交于点O,下列条件中不能用作判定该四边形是平行四边形条件的是( )A、AB=CD B、AC=BD C、AD∥BC D、OA=OC10. 如图,正比例函数y=x与反比例y= 的图象相交于A、C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为( )
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当AC=BD时,它是矩形 D、当∠ABC=90°时,它是正方形8. 某校八年级学生去距学校10km的科技馆参观,一部分学生骑自行车,过了30min,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑自行车学生速度的4倍,设骑自行车学生的速度为xkm/h,则下列方程正确的是( )A、 B、 C、 D、9. 已知四边形ABCD中,AB∥CD,对角线AC与BD交于点O,下列条件中不能用作判定该四边形是平行四边形条件的是( )A、AB=CD B、AC=BD C、AD∥BC D、OA=OC10. 如图,正比例函数y=x与反比例y= 的图象相交于A、C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为( )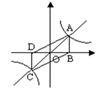 A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
11. 计算: =.12. 若正比例函数y=kx的图象经过点(2,4),则k=.13. ▱ABCD中,∠A=50°,则∠D= .14. 在 中,对角线 , 相交于点 ,若 , , ,则 的周长为.15. 如图,在矩形 中,对角线 与 相交于点 , , ,则 的长为.
 16. 平面直角坐标系中,点O为坐标原点,菱形OABC中的顶点B在x轴的正半轴上,点A在反比例函数y= (x>0)的图象上,点C的坐标为(3,﹣4).(1)、点A的坐标为;(2)、若将菱形OABC沿y轴正方向平移,使其某个顶点落在反比例函数y= (x>0)的图象上,则该菱形向上平移的距离为.
16. 平面直角坐标系中,点O为坐标原点,菱形OABC中的顶点B在x轴的正半轴上,点A在反比例函数y= (x>0)的图象上,点C的坐标为(3,﹣4).(1)、点A的坐标为;(2)、若将菱形OABC沿y轴正方向平移,使其某个顶点落在反比例函数y= (x>0)的图象上,则该菱形向上平移的距离为.三、解答题
-
17. 计算: .18. 解方程: .19. 某校举办“书香校园”读书活动,经过对八年级(2)班的全体学生的每人每月读书的数量(单位:本)进行统计分析,得到条形统计图如图所示:
 (1)、填空:该班学生读书数量的众数是本,中位数是本;(2)、求该班学生每月的平均读书数量?(结果精确到0.1)20. 学期末,某班评选一名优秀学生干部,下表是班长、学习委员和团支部书记的得分情况:
(1)、填空:该班学生读书数量的众数是本,中位数是本;(2)、求该班学生每月的平均读书数量?(结果精确到0.1)20. 学期末,某班评选一名优秀学生干部,下表是班长、学习委员和团支部书记的得分情况: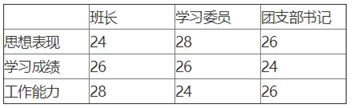
假设在评选优秀干部时,思想表现、学习成绩、工作能力这三方面的重要比为3 ∶3 ∶4 ,通过计算说明谁应当选为优秀学生干部。
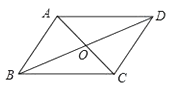
21. 如图,直线y= x+b,分别交x轴,y轴于点A、C,点P是直线AC与双曲线y= 在第一象限内的交点,过点P作PB⊥x轴于点B,若OB=2,PB=3. (1)、填空:k=;(2)、求△ABC的面积;(3)、求在第一象限内,当x取何值时,一次函数的值小于反比例函数的值?22. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)、填空:k=;(2)、求△ABC的面积;(3)、求在第一象限内,当x取何值时,一次函数的值小于反比例函数的值?22. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.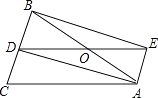 (1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由23. 小东到学校参加毕业晚会演出,到学校时发现演出道具还放在家中,此时距毕业晚会开始还有25分钟,于是立即步行回家.同时,他父亲从家里出发骑自行车以他3倍的速度给他送道具,两人在途中相遇,相遇后,小东父亲立即骑自行车以原来的速度载小东返回学校.图中线段AB、OB表示相遇前(含相遇)父亲送道具、小东取道具过程中,各自离学校的路程S(米)与所用时间t分)之间的函数关系,结合图象解答下列问题.
(1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由23. 小东到学校参加毕业晚会演出,到学校时发现演出道具还放在家中,此时距毕业晚会开始还有25分钟,于是立即步行回家.同时,他父亲从家里出发骑自行车以他3倍的速度给他送道具,两人在途中相遇,相遇后,小东父亲立即骑自行车以原来的速度载小东返回学校.图中线段AB、OB表示相遇前(含相遇)父亲送道具、小东取道具过程中,各自离学校的路程S(米)与所用时间t分)之间的函数关系,结合图象解答下列问题.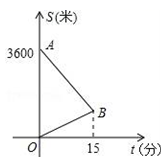 (1)、求点B坐标;(2)、求AB直线的解析式;(3)、小东能否在毕业晚会开始前到达学校?
(1)、求点B坐标;(2)、求AB直线的解析式;(3)、小东能否在毕业晚会开始前到达学校?