青岛版九年级上册数学第二章《解直角三角形》测试题
试卷更新日期：2020-09-13 类型：单元试卷
一、单选题
-
1. 如图，在坡度为 的山坡上种树，要求相邻两棵树的水平距离是6m，则斜坡上相邻两棵树的坡面距离是（ ）
A、3m B、3 m C、12m D、6m2. 如图，一架无人机航拍过程中在 处测得地面上 ， 两个目标点的俯角分别为 和 .若 ， 两个目标点之间的距离是100米，则此时无人机与目标点 之间的距离（即 的长）为（ ）
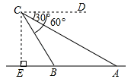A、100米 B、 米 C、50米 D、 米3. 如图，轮船沿正南方向以30海里/时的速度匀速航行，在M处观测到灯塔P在西偏南68°方向上，航行2小时后到达N处，观测灯塔P在西偏南46°方向上，若该船继续向南航行至离灯塔最近位置，则此时轮船离灯塔的距离约为(由科学计算器得到sin68°≈0.9272，sin46°≈0.7193，sin22°≈0.3746，sin44°≈0.6947)（ ）
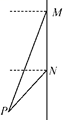A、22.48海里 B、41.68海里 C、43.16海里 D、55.63海里4. 如图，小明想要测量学校操场上旗杆 的高度，他作了如下操作：（1）在点C处放置测角仪，测得旗杆顶的仰角 ；（2）量得测角仪的高度 ；（3）量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识，旗杆的高度可表示为（ ）
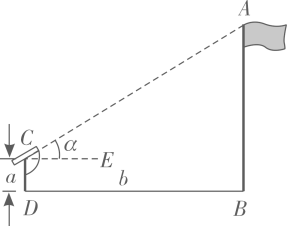A、 B、 C、 D、5. 如图，一棵珍贵的树倾斜程度越来越厉害了．出于对它的保护，需要测量它的高度，现采取以下措施：在地面上选取一点C，测得∠BCA=37°，AC=28米，∠BAC=45°，则这棵树的高AB约为（参考数据：sin37°≈ ，tan37°≈ ， ≈1.4）（ ）
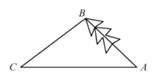A、14米 B、15米 C、17米 D、18米6. 如图，轮船在A处观测灯塔C位于北偏西70°方向上，轮船从A处以每小时40海里的速度沿南偏西50°方向匀速航行，1小时后到达码头B处，此时，观测灯塔C位于北偏西25°方向上，则灯塔C与码头B的距离是（ ）
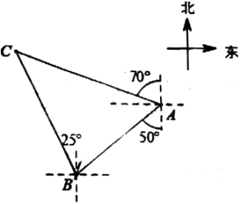A、20 海里 B、10 海里 C、20 海里 D、10 海里7. 如图，A，B两景点相距20km，C景点位于A景点北偏东60°方向上，位于B景点北偏西30°方向上，则A，C两景点相距（ ）
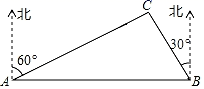A、10km B、10 km C、10 km D、 km8. 如图，在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡，山坡CD的坡度（或坡比）i＝1：0.75，山坡坡底C点到坡顶D点的距离CD＝45m，在坡顶D点处测得居民楼楼顶A点的仰角为28°，居民楼AB与山坡CD的剖面在同一平面内，则居民楼AB的高度约为（参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）（ ）
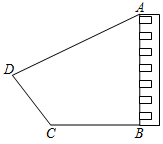A、76.9m B、82.1m C、94.8m D、112.6m9. 如图，从点 看一山坡上的电线杆 ，观测点 的仰角是45°，向前走 到达 点，测得顶端点 和杆底端点 的仰角分别是60°和30°，则该电线杆 的高度（ ）
A、 B、 C、 D、10. 某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求，游客可以乘坐垂直升降电梯AB自由上下选择项目难度.其中斜坡轨道BC的坡度（或坡比）为i＝1：2，BC＝12 米，CD＝8米，∠D＝36°，（其中点A，B，C，D均在同一平面内）则垂直升降电梯AB的高度约为（ ）米.（精确到0.1米，参考数据：tan36°≈0.73，cos36°≈0.81，sin36°≈0.59）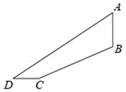
A、5.6 B、6.9 C、11.4 D、13.911. 某货站用传送带传送货物，为了提高传送过程的安全性，工人师傅将原坡角45°的传送带AB，调整为坡度i＝1： 的新传送带AC（如图所示）．已知原传送带AB的长是4 米，那么新传送带AC的长是（ ）
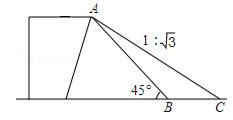A、8米 B、4米 C、6米 D、3米12. 如图，学校环保社成员想测量斜坡CD旁一棵树AB的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知斜坡CD的长度为10m，DE的长为5m，则树AB的高度是（ ）m.
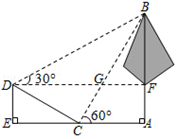A、10 B、15 C、15 D、15 ﹣5二、填空题
-
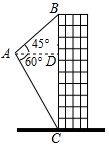
13. 如图，航模小组用无人机来测量建筑物BC的高度，无人机从A处测得建筑物顶部B的仰角为45°，测得底部C的俯角为60°，若此时无人机与该建筑物的水平距离AD为30m，则该建筑物的高度BC为m.（结果保留根号）
14. 如图，点C在线段 上，且 ，分别以 、 为边在线段 的同侧作正方形 、 ，连接 、 ，则 .
15. 如图，对折矩形纸片ABCD使AD与BC重合，得到折痕MN，再把纸片展平.E是AD上一点，将△ABE沿BE折叠，使点A的对应点A′落在MN上.若CD＝5，则BE的长是.
16. 如图，小明在距离地面30米的P处测得A处的俯角为15°，B处的俯角为60°．若斜面坡度为1： ，则斜坡AB的长是米．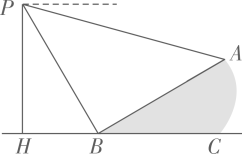
17. 如图，在 的正方形网格中，每个小正方形的边长都是1， 的顶点都在这些小正方形的顶点上，则 的值为 ．
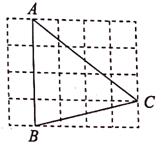18. 计算sin60°tan60°- cos45°cos60°的结果为 。19. 如图，是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧OB与墙MN平行且距离为0.8米，一辆小汽车车门宽AO为1.2米，当车门打开角度∠AOB为40°时，车门是否会碰到墙？；(填“是”或“否”)请简述你的理由.(参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84)
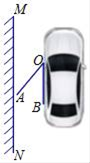20. 如图，已知sinO＝ ，OA＝6，点P是射线ON上一动点，当△AOP为直角三角形时，则AP＝.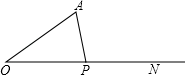
三、解答题
-
21.
假日，小强在广场放风筝．如图，小强为了计算风筝离地面的高度，他测得风筝的仰角为60°，已知风筝线BC的长为10米，小强的身高AB为1.55米，请你帮小强画出测量示意图，并计算出风筝离地面的高度．（结果精确到1米，参考数据 ≈1.41， ≈1.73 ）
22. 汉江是长江最长的支流，在历史上占居重要地位，陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽，如图，探测器在A处观测到正前方汉江两岸岸边的B、C两点，并测得B、C两点的俯角分别为45°，30°已知A处离地面的高度为80m，河平面BC与地面在同一水平面上，请你求出汉江该段河宽BC.(结果保留根号)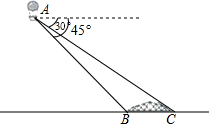
23. 如图，海面上一艘船由西向东航行，在A处测得正东方向上一座灯塔的最高点C的仰角为31°，再向东继续航行35m到达B处，测得该灯塔的最高点C的仰角为45°.根据测得的数据，计算这座灯塔的高度CD（结果精确到0.1）.参考数据：sin31° 0.52， ， .
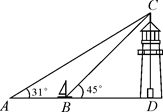24. 如图，在△ABC中，BD⊥AC，AB＝6，AC＝5 ，∠A＝30°.
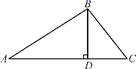(1)、求BD和AD的长；(2)、求tanC的值.25. 某市为了加快5G网络信号覆盖，在市区附近小山顶架设信号发射塔，如图所示.小军为了知道发射塔的高度，从地面上的一点A测得发射塔顶端P点的仰角是45°，向前走60米到达B点测得P点的仰角是60°，测得发射塔底部Q点的仰角是30°.请你帮小军计算出信号发射塔PQ的高度.（结果精确到0.1 米， ）
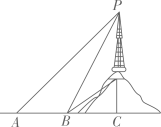26. 如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角为45°，沿斜坡走3 米到达斜坡上点D，在此处测得树顶端点B的仰角为30°，且斜坡AF的坡比为1：2．求大树BC的高度约为多少米？（ ≈1.732，结果精确到0.1）
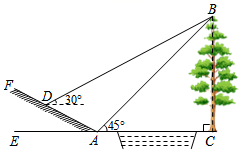27. 如图，A城气象台测得台风中心在A城的正西方300千米处，以每小时10 千米的速度向北偏东60°的BF方向移动，距台风中心200千米的范围内是受这次台风影响的区域．
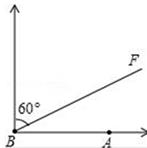(1)、问A城是否会受到这次台风的影响？为什么？(2)、若A城受到这次台风的影响，那么A城遭受这次台风影响的时间有多长？28. 如图，在大楼AB的正前方有一斜坡CD，CD=13米，坡度为1： ，高为DE，在斜坡下的点C处测得楼顶B的仰角为64°，在斜坡上的点D处测得楼顶B的仰角为45°，其中A、C、E在同一直线上．
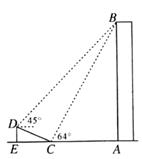(1)、求斜坡CD的高度DE；(2)、求大楼AB的高度；（参考数据：sin64°≈0.9，tan64°≈2)．