山东省济宁市微山县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-11 类型:期末考试
一、单选题
-
1. 下列各式是最简二次根式的是( )A、 B、 C、 D、2. 下列函数中, 是 的一次函数的是( )A、 B、 C、 D、3. 一组数据2, ,-2,1,3的平均数是0.8,则 的值是( )A、-3.2 B、-1 C、0 D、14. 已知点 在第二象限,直线 经过 , 两点,那么 与 的大小关系是( )A、 B、 C、 D、5. 如图,点 是 的边 上一动点,过点 分别作 , 垂足为 , ,连接 ,已知 , , ,当点 运动到 中点时, 等于( )
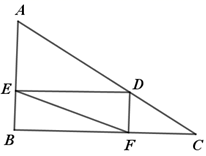 A、6 B、8 C、10 D、146. 已知正比例函数y=kx的图象经过第二、四象限,则一次函数y=kx﹣k的图象可能是图中的( )A、
A、6 B、8 C、10 D、146. 已知正比例函数y=kx的图象经过第二、四象限,则一次函数y=kx﹣k的图象可能是图中的( )A、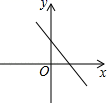 B、
B、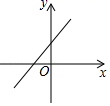 C、
C、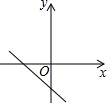 D、
D、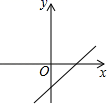 7. 已知平行四边形 的对角线相交于点 ,补充下列四个条件,能使平行四边形 成为菱形的是( )
7. 已知平行四边形 的对角线相交于点 ,补充下列四个条件,能使平行四边形 成为菱形的是( )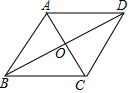 A、 B、 C、 D、8. 如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )
A、 B、 C、 D、8. 如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )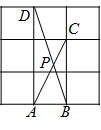 A、 B、 C、 D、9. 按照如图所示的程序计算函数 的值时,若输入 的值是3,则输出 的值是7,若输入 的值是1,则输出 的值是( )
A、 B、 C、 D、9. 按照如图所示的程序计算函数 的值时,若输入 的值是3,则输出 的值是7,若输入 的值是1,则输出 的值是( )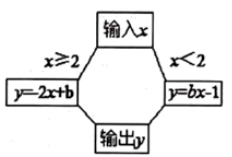 A、-3 B、-2 C、0 D、210. 在学完二次根式的乘除法之后,小明借助计算机完成了以下计算: , , , ,……,通过计算,小明发现了其中规律,那么按照上述规律,计算 的结果是( )A、 B、 C、 D、
A、-3 B、-2 C、0 D、210. 在学完二次根式的乘除法之后,小明借助计算机完成了以下计算: , , , ,……,通过计算,小明发现了其中规律,那么按照上述规律,计算 的结果是( )A、 B、 C、 D、二、填空题
-
11. 已知函数 ,那么自变量 的取值范围是 .12. 新型冠状病毒疫情复工、复产后,某商场为了刺激消费,实施薄利多销,减少库存,现将一商品在保持销售价60元/件不变的前提下,规定凡购买超过5件者,超出的部分打6折出售,若顾客购买 件,应付 元,则 与 之间的函数关系式是 .13. 已知直线 与直线 的交点坐标为 ,则关于 的不等式 的解集是 .
 14. 边长为4的菱形 在平面直角坐标系中的位置如图所示,点 在 轴的负半轴上, ,点 是 轴上一动点,当 的值最小时,点 的坐标是 .
14. 边长为4的菱形 在平面直角坐标系中的位置如图所示,点 在 轴的负半轴上, ,点 是 轴上一动点,当 的值最小时,点 的坐标是 . 15. 若 ,则代数式 的值为 .
15. 若 ,则代数式 的值为 .三、解答题
-
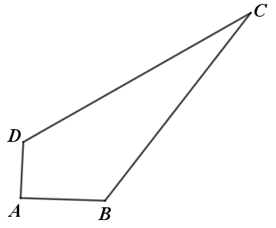
16. 计算:17. 2019年6月16日,某校数学兴趣小组参加社会实践活动,他们途中发现一块四边形草地(如图所示四边形 ),借助所带工具测得: 米, 米, 米, 米, .
请你和他们一起计算出这块草地的面积.
 18. 某校为了解八年级学生对“防溺水”安全知识的掌握情况,从八年级一班和二班各随机抽取10名学生进行比赛,并依据成绩(十分制,单位:分)绘制了下列统计图.
18. 某校为了解八年级学生对“防溺水”安全知识的掌握情况,从八年级一班和二班各随机抽取10名学生进行比赛,并依据成绩(十分制,单位:分)绘制了下列统计图.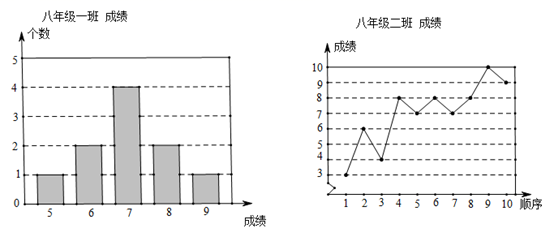
根据以上统计图,进行整理、描述和分析,制作了统计表(如下表):
项目
班级
平均分
中位数
众数
方差
八年级一班
7
7
八年级二班
7.5
4.2
(1)、求表格中的 , , , 的值;(2)、你认为哪个班级的成绩比较稳定?19. 疫情复学后,某校借助小型飞行器监测学生课间休息情况,及时制止学生聚集现象,一天,甲飞行器从5 高度,以1 的速度上升;与此同时,乙飞行器从15 高度,以0.5 的速度上升,两个飞行器都匀速上升了1 .(1)、分别写出甲、乙两个飞行器所在高度 (单位: )与上升时间为 (单位: )之间的函数关系式,并写出自变量 的取值范围;(2)、当 时,甲、乙两个飞行器的高度相差多少米?(3)、在某时刻甲、乙两个飞行器能否位于同一高度?如果能,求此时两个飞行器高度.20. 如图,点 、 分别是正方形 边 , 延长线上的点,且 ,连接 ,过点 作 ,使 ,连接 , , 与 相交于点 .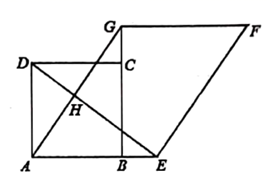 (1)、求证: ;(2)、猜想: 与 的数量关系和位置关系,并证明你的猜想.21. 知识经验
(1)、求证: ;(2)、猜想: 与 的数量关系和位置关系,并证明你的猜想.21. 知识经验我们知道,如果两个因式的积为0,那么这两个因式中至少有一个等于0;反之,如果两个因式中任何一个为0,那么它们的积也等于0.
即:如果 ,那么 或
知识迁移
Ⅰ.解方程:
解: ,
或 ,
∴ 或 .
Ⅱ.解方程: ,
解: ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 或 ,
∴ 或 .
理解应用
(1)、解方程:(2)、拓展应用如图,有一块长宽分别为80 ,60 的矩形硬纸板,在它的四个角上分别剪去四个相同的小正方形,然后将四周突出的部分折起来,就可以做成底面积为1500 的无盖的长方体盒子,求所剪去的小正方形的边长.
 22. 如图,在平面直角坐标系第一象限内有矩形 , 轴,过 , 两点作直线 ,已知 , ,点 坐标为 .
22. 如图,在平面直角坐标系第一象限内有矩形 , 轴,过 , 两点作直线 ,已知 , ,点 坐标为 .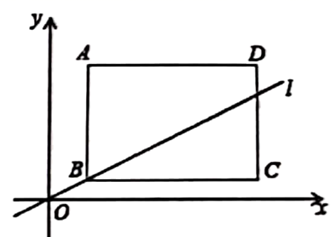 (1)、填空:点 的坐标是 , 点 的坐标是 , 点 的坐标是;(2)、若直线 沿 轴上下平移,当直线 与矩形 有且只有一个公共点时,直接写出此时直线的解析式;(3)、在(2)中平移过程中,设直线 与 轴, 轴交点为 , ,那么直线 是否会平分矩形 的面积?若会,画出此时直线 (不需证明)并求出 的面积;若不会,请说明理由.
(1)、填空:点 的坐标是 , 点 的坐标是 , 点 的坐标是;(2)、若直线 沿 轴上下平移,当直线 与矩形 有且只有一个公共点时,直接写出此时直线的解析式;(3)、在(2)中平移过程中,设直线 与 轴, 轴交点为 , ,那么直线 是否会平分矩形 的面积?若会,画出此时直线 (不需证明)并求出 的面积;若不会,请说明理由.