山东省济南市天桥区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-11 类型:期末考试
一、单选题
-
1. 下面四个图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算结果为a6的是( )
2. 下列计算结果为a6的是( )
A、a7﹣a B、a2•a3 C、a8÷a2 D、(a4)23. 已知三角形中,某两条边的长分别为4和9则另一条边的长可能是( )A、4 B、5 C、12 D、134. 将0.00000125米用科学记数法表示是( )米A、1.25×10-7 B、1.25×10-6 C、12.5×10-6 D、1.25×1075. 如图是反映两个变量关系的图,下列的四个情境比较合适该图的是( ) A、一杯热水放在桌子上,它的水温与时间的关系 B、一辆汽车从起动到匀速行驶,速度与时间的关系 C、一架飞机从起飞到降落的速度与时晨的关系 D、踢出的足球的速度与时间的关系6. 如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF,如果∠1=32°,那么∠2的度数是( )
A、一杯热水放在桌子上,它的水温与时间的关系 B、一辆汽车从起动到匀速行驶,速度与时间的关系 C、一架飞机从起飞到降落的速度与时晨的关系 D、踢出的足球的速度与时间的关系6. 如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF,如果∠1=32°,那么∠2的度数是( )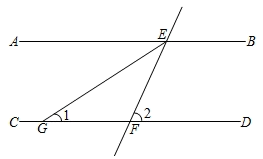 A、64° B、68° C、58° D、60°7. 如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为( )
A、64° B、68° C、58° D、60°7. 如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为( ) A、45° B、60° C、90° D、100°8. 在△ABC中,AB=6,AC=8,BC=10,则该三角形为( )
A、45° B、60° C、90° D、100°8. 在△ABC中,AB=6,AC=8,BC=10,则该三角形为( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形9. 如图,若△ABC与△DEF关于直线l对称,BE交l于点O , 则下列说法不一定正确的是( )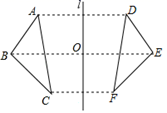 A、AB∥EF B、AC=DF C、AD⊥l D、BO=EO10. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球,下列事件是必然事件的是( )A、摸出的三个球中至少有一个球是黑球 B、摸出的三个球中至少有一个球是白球 C、摸出的三个球中至少有两个球是黑球 D、摸出的三个球中至少有两个球是白球11. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、AB∥EF B、AC=DF C、AD⊥l D、BO=EO10. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球,下列事件是必然事件的是( )A、摸出的三个球中至少有一个球是黑球 B、摸出的三个球中至少有一个球是白球 C、摸出的三个球中至少有两个球是黑球 D、摸出的三个球中至少有两个球是白球11. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD12. 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )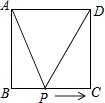 A、
A、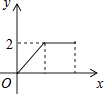 B、
B、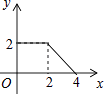 C、
C、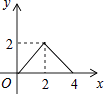 D、
D、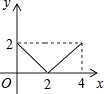
二、填空题
-
13. 计算:(a+2)(a-2)=;14. 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为12,则图中△BEF的面积为。
 15. 如图,小明向图中的格盘中随意投掷一枚棋子,该棋子落在三角形内的概率是;
15. 如图,小明向图中的格盘中随意投掷一枚棋子,该棋子落在三角形内的概率是;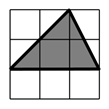 16. 如图,AB、CD表示两根长度相同的木条,若O是AB、CD的中点,经测量AC=9cm,则容器的内径DB为cm.
16. 如图,AB、CD表示两根长度相同的木条,若O是AB、CD的中点,经测量AC=9cm,则容器的内径DB为cm. 17. 若4x2-mx+1是完全平方式,则m的值是。18. 如图,BE和CE分别为 的内角∠ABC和外角∠ACD的平分线,BE⊥AC于点H,CF平分∠ACB交BE于点F,连接AE,则下列结论:①∠ECF=90°;②AE=CE;③∠BFC=90°+ ∠BAC;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的为;
17. 若4x2-mx+1是完全平方式,则m的值是。18. 如图,BE和CE分别为 的内角∠ABC和外角∠ACD的平分线,BE⊥AC于点H,CF平分∠ACB交BE于点F,连接AE,则下列结论:①∠ECF=90°;②AE=CE;③∠BFC=90°+ ∠BAC;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的为;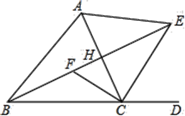 19. 如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
19. 如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
①图2中的阴影部分的面积为;
②观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是;
③根据(2)中的结论,若x+y=5,x•y= ,则(x﹣y)2=;
④实际上通过计算图形的面积可以探求相应的等式.
如图3,你发现的等式是 .
三、解答题
-
20. 计算:(1)、(-1)2020+(- )-2-(3.14-π)0;(2)、a3×a5+(a2)4-3a8;21. 先化简,再求值: (a+3)2+(1+a)(1-a),其中a= .22. 推理填空:
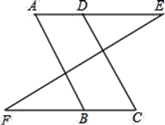
如图,已知∠A=∠C,∠E=∠F, 试说明AB//CD.
证明:∵∠E=∠F,( ▲ )
∴AE//CF,( ▲ )
∴∠A=∠ABF.( ▲ )
∵∠A=∠C.( ▲ )
∴∠ABF=∠C( ▲ )
∴AB//CD.( ▲ )
23. 如图,∠FED=∠B,EF=BC,DA= EB.求证:∠F=∠C.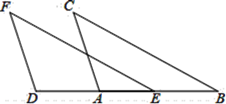 24. 如图,网格中有一个格点△ABC(即三角形的顶点都在格点上).每个小正方形的边长为1.
24. 如图,网格中有一个格点△ABC(即三角形的顶点都在格点上).每个小正方形的边长为1.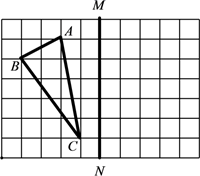 (1)、在图中作出△ABC关于直线MN对称的△A1B1C1(要求A与A1 , B与B1 , C与C1相对应);(2)、在直线MN上找一点P,使得△PAC的周长最小;(3)、求△ABC的面积.25. 小丽和小刚都想参加学校组织的暑期实践活动,但只有一个名额,小丽提议:将一个转盘9等分,分別将9个区间标上1至9个9号码,随意转动-次转盘,根据指针指向区间决定谁去参加活动,具体规则:若指针指向偶数区间,小刚去参加活动;若指针指向奇数区间,小丽去参加活动.
(1)、在图中作出△ABC关于直线MN对称的△A1B1C1(要求A与A1 , B与B1 , C与C1相对应);(2)、在直线MN上找一点P,使得△PAC的周长最小;(3)、求△ABC的面积.25. 小丽和小刚都想参加学校组织的暑期实践活动,但只有一个名额,小丽提议:将一个转盘9等分,分別将9个区间标上1至9个9号码,随意转动-次转盘,根据指针指向区间决定谁去参加活动,具体规则:若指针指向偶数区间,小刚去参加活动;若指针指向奇数区间,小丽去参加活动.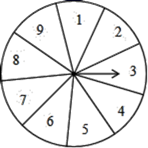 (1)、求小刚去参加活动的概率是多少?(2)、你认为这个游戏公平吗?请说明理由.26. 小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图).
(1)、求小刚去参加活动的概率是多少?(2)、你认为这个游戏公平吗?请说明理由.26. 小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图).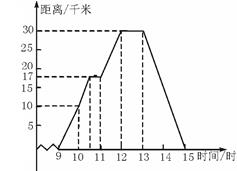 (1)、图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2)、10时和13时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、11时到12时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?27. 如图,在 中, 为锐角,点 为射线 上一动点,连接 .以 为直角边且在 的上方作等腰直角三角形 .
(1)、图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2)、10时和13时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、11时到12时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?27. 如图,在 中, 为锐角,点 为射线 上一动点,连接 .以 为直角边且在 的上方作等腰直角三角形 .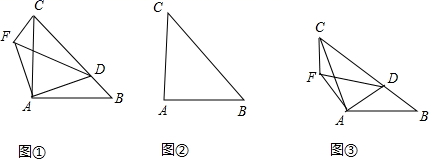 (1)、若 ,
(1)、若 ,①当点 在线段 上时(与点 不重合),试探讨 与 的数量关系和位置关系;
②当点 在线段 的延长线上时,①中的结论是否仍然成立,请在图2中面出相应的图形并说明理由;
(2)、如图3,若 , , ,点 在线段 上运动,试探究 与 的位置关系.