山东省济南市平阴县2019-2020学年七年级下学期数学期末试卷
试卷更新日期：2020-09-11 类型：期末考试
一、单选题
-
1. 下列标志中，可以看作是轴对称图形的是（ ）A、
B、
C、
D、
2. 将0.000613用科学记数法表示应为（ ）A、6.13×10－4 B、0.613×10－4 C、6.13×10－5 D、613×10－43. 下列计算中：①(2x)3·(－5x2y)＝－10x5y；②(2a2－b)(2a2＋b)＝4a2－b2；③(x＋3)(3－x)＝x2－9；④(－x＋y)(x＋y)＝－(x－y)(x＋y)＝－x2－y2 ． 其中错误的有（ ）A、1个 B、2个 C、3个 D、4个4. 如图，窗户打开后，用窗钩AB可将其固定，其所运用的几何原理是（ ）
A、三角形的稳定性 B、垂线段最短 C、两点确定一条直线 D、两点之间，线段最短5. 若是x2＋(m－1)x＋9是完全平方式，则m的值是（ ）A、7 B、－5 C、±6 D、7或－56. 如图，直线AB、CD相交于点O，EO⊥CD，下列说法错误的是（ ）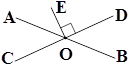
A、∠AOD＝∠BOC B、∠AOE＋∠BOD＝90° C、∠AOC＝∠AOE D、∠AOD＋∠BOD＝180°7. 将一直角三角尺与两边平行的纸条按如图所示放置，下列结论：
①∠1=∠2；②∠3=∠4；③∠2+∠4=90°；④∠4+∠5=180°.正确的个数是（ ）
A、1 B、2 C、3 D、48. 若│x＋y－5│＋(xy－3)2＝0，则x2＋y2的值为（ ）A、19 B、31 C、27 D、239. 一枚质地均匀的正方体骰子，其六个面上分别刻有1，2，3，4，5，6六个数字，投掷这个骰子一次，得到的点数与3、4作为三角形三边的长，能构成三角形的概率是（ ）A、 B、 C、 D、10. 如图，若AB∥CD ， 则∠A、∠E、∠D之间的是（ ）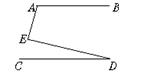
A、∠A+∠E+∠D=180° B、∠A+∠E－∠D=180° C、∠A－∠E+∠D=180° D、∠A+∠E+∠D=270°11. 如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（ ）
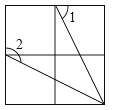A、150° B、180° C、210° D、225°12. 如图，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三角形中y与n之间的关系是（ ）
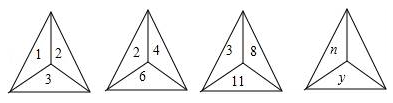A、y=2n+1 B、y=2n+n C、y=2n+1+n D、y=2n+n+1二、填空题
-
13. 计算：(a－
b)2＝； 14. 如果(3m＋n＋3)(3m ＋n－3)＝40，则3m ＋n的值为；15. 如图，已知：∠A＝∠D，∠1＝∠2，下列条件中：①∠E＝∠B；②EF＝ BC；③AB＝ EF；④AF＝CD．能使△ABC≌△DEF的有；(填序号)
16. 如图所示，一个角60°的三角形纸片，剪去这个60°角后，得到一个四边形，则∠1+∠2＝ ．
17. 如图，△ABC中，点D、E分别在边AB、AC的中点，将△ADE沿过DE折叠，使点A落在BC上F处，若∠B=50°，则∠BDF=.
18. 如图，在△ABE和△ACF中，EB交AC于点M，交FC于点D，AB交FC于点N，∠E=∠F=90°，∠B=∠C，AE=AF.下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN.其中，正确的是 ． (填序号)
三、解答题
-
19. 计算(1)、(－2a2)2·(3ab2－5ab＋1)；(2)、(π－2020)0＋( )2018×(－ )2020＋(－2)-220. 先化简，再求值：
[（2x﹣y）2+（2x﹣y）（2x+y）+8xy]÷4x ， 其中x＝﹣ ，y＝4
21. 如图，C ， F是线段AB上的两点，AF＝BC ， CD∥BE ， ∠D＝∠E ．求证：AD＝FE ．
22. 如图，点G在CA的延长线上，AF＝AG ， AD⊥BC ， GE⊥BC．求证：AD平分∠BAC．
证明：∵AF＝AG(已知)，
∴∠AGF＝∠AFG( ▲ )
∵AD⊥BC ， GE⊥BC(已知)，
∴∠ADC＝∠GEC＝90°( ▲ )
∴AD GE( ▲ )
∴∠CAD＝ ▲ (两直线平行，同位角相等)．
∠BAD＝∠AFG( ▲ )
∴∠CAD＝∠BAD (等量代换)
∴AD平分∠BAC( ▲ )
23. 小亮和小芳都想参加学校杜团组织的暑假实践活动，但只有一个名额，小亮提议用如下的办法决定谁去参加活动：将一个转盘9等分，分别标上1至9九个号码，随意转动转盘，若转到2的倍数，小亮去参加活动；转到3的倍数，小芳去参加活动；转到其它号码则重新转动转盘.
(1)、转盘转到2的倍数的概率是多少？；(2)、你认为这个游戏公平吗？请说明理由.24. “龟兔赛跑”的故事同学们都非常热悉，图中的线段OD和折线OABC分别表示龟兔赛跑时路程与时间的关系，请你根据图中给出的信息，解决下列问题．
(1)、填空：折线OABC表示赛跑过程中(填“兔子”或“乌龟”)的路程与时间的关系，赛跑的全过程是米．(2)、兔子在起初每分钟跑多少米？乌龟每分钟爬多少米？(3)、乌龟用了多少分钟追上了正在睡觉的兔子？(4)、兔子醒来后，以400米/分的速度跑向终点，结果还是比乌龟晚到了1分钟，请你算算兔子中间停下睡觉用了多少分钟．25. 看图回答问题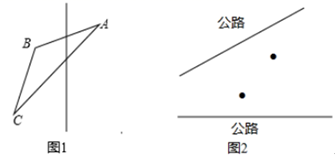
(1)、如图，作出△ABC 关于直线l的对称图形；(2)、现有两条高速公路和A、B两个城镇(如图)，准备建立一个燃气中心站P ， 使中心站到两条公路距离相等，并且到两个城镇距离相等，请你画出中心站位置．26. 某学习小组在探究三角形全等时，发现了下面这种典型的基本图形：
(1)、如图1，在△ABC中，∠BAC＝90° ， AB＝AC ， 直线m经过点A ， BD⊥直线m ， CE⊥直线m ， 垂足分别为点D、E ． 试猜想DE、 BD、CE 有怎样的数量关系，并说明理由．(2)、组员小颖想，如果三个角不是直角，那结论是否成立呢？如图2，将(1)中的条件改为：在△ABC中，AB＝AC ， D、A、B三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α (其中α为任意锐角或钝角)．如果成立，请你给出推理过程；若不成立，请说明理由．
27. 已知Rt△ABC和Rt△DBE ， ∠ABC＝∠DBE＝90°，AB＝CB ， DB＝EB ， CE所在的直线交AD于点F ．
(1)、如图1，若点D在△ABC外，点B在AB边上，求证：AD＝CE ， AD⊥CE ．(2)、若将图1中的△DBE绕点B顺时针旋转，使点B在△ABC内部，如图2，求证：AD＝CE ， AD⊥CE ．(3)、若将图1中的△DBE绕点B逆时针旋转，使点D、E都在△ABC外部，如图3，请直出AD和CE的数量和位置关系．