山东省济南市槐荫区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-11 类型:期末考试
一、单选题
-
1. 如图,四个图标分别是剑桥大学、北京大学、浙江大学和北京理工大学的校徽的重要组成部分,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某种微粒的直径为0.000058米,那么该微粒的直径用科学记数法可以表示为( )A、0.58×10-6米 B、5.8×10-5米 C、58×10-6米 D、5.8×10-6米3.
2. 某种微粒的直径为0.000058米,那么该微粒的直径用科学记数法可以表示为( )A、0.58×10-6米 B、5.8×10-5米 C、58×10-6米 D、5.8×10-6米3.如图,在所标识的角中,互为对顶角的两个角是( )
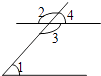 A、∠2和∠3 B、∠1和∠3 C、∠1和∠4 D、∠1和∠24. 骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是( )A、沙漠 B、体温 C、时间 D、骆驼5. 下列式子运算正确的是( )A、(a2)3=a6 B、a6×a3=a3 C、(a-b)2=a2-b2 D、a2+a2=a46. 若一个三角形三个内角度数的比为2:3:4,那么这个三角形是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形7. 下列事件中属于不确定事件的是( )A、抛出的篮球会落下 B、从装有黑球,白球的袋里摸出红球 C、367人中至少有2人是同月同日出生 D、买1张彩票,中500万大奖8. 已知等腰三角形两边长分别为2和4,则此等腰三角形的周长是( )A、10 B、8 C、8或10 D、7或89. 在一次小制作活动中,艳艳剪了一个燕尾图案(如图所示),她用刻度尺量得AB=AC , BO=CO , 为了保证图案的美观,她准备再用量角器量一下∠B和∠C是否相等,小麦走过来说:“不用量了,肯定相等”,小麦的说法利用了判定三角形全等的方法是( )
A、∠2和∠3 B、∠1和∠3 C、∠1和∠4 D、∠1和∠24. 骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是( )A、沙漠 B、体温 C、时间 D、骆驼5. 下列式子运算正确的是( )A、(a2)3=a6 B、a6×a3=a3 C、(a-b)2=a2-b2 D、a2+a2=a46. 若一个三角形三个内角度数的比为2:3:4,那么这个三角形是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形7. 下列事件中属于不确定事件的是( )A、抛出的篮球会落下 B、从装有黑球,白球的袋里摸出红球 C、367人中至少有2人是同月同日出生 D、买1张彩票,中500万大奖8. 已知等腰三角形两边长分别为2和4,则此等腰三角形的周长是( )A、10 B、8 C、8或10 D、7或89. 在一次小制作活动中,艳艳剪了一个燕尾图案(如图所示),她用刻度尺量得AB=AC , BO=CO , 为了保证图案的美观,她准备再用量角器量一下∠B和∠C是否相等,小麦走过来说:“不用量了,肯定相等”,小麦的说法利用了判定三角形全等的方法是( ) A、ASA B、SAS C、AAS D、SSS10. 正方形地板由9块边长均相等的小正方形组成,米粒随机地撒在如图所示的正方形地板上,那么米粒最终停留在黑色区城的概率是( )
A、ASA B、SAS C、AAS D、SSS10. 正方形地板由9块边长均相等的小正方形组成,米粒随机地撒在如图所示的正方形地板上,那么米粒最终停留在黑色区城的概率是( )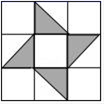 A、 B、 C、 D、11. 某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水. 某同学用直线(虛线) 表示小河, 两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( ).A、
A、 B、 C、 D、11. 某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水. 某同学用直线(虛线) 表示小河, 两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( ).A、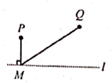 B、
B、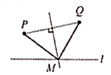 C、
C、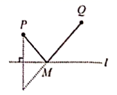 D、
D、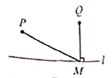 12. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )
12. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的底角度数是( )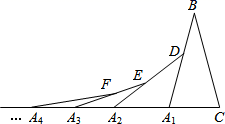 A、( )n•75° B、( )n﹣1•65° C、( )n﹣1•75° D、( )n•85°
A、( )n•75° B、( )n﹣1•65° C、( )n﹣1•75° D、( )n•85°二、填空题
-
13. 计算:3-2=;14. 一蜡烛高20 厘米,点燃后平均每小时燃掉4厘米,则蜡烛点燃后剩余的高度h(厘米)与燃烧时间t(时)之间的关系式是(0≤t≤5).15. 如图所示,直线PQ∥MN,C是MN上一点,CE交PQ于A,CF交PQ于B,且∠ECF=90°,如果∠FBQ=50°,则∠ECM的度数为;
 16. 小颖妈妈经营的玩具店某次进了一箱黑白两种颜色的塑料球3000个,为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近波动,据此可以估计黑球的个数约是.17. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是;
16. 小颖妈妈经营的玩具店某次进了一箱黑白两种颜色的塑料球3000个,为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近波动,据此可以估计黑球的个数约是.17. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是;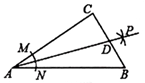 18. 如图,△DAC和△EBC均是等边三角形,A、C、B三点共线,AE与BD相交于点P , AE与BD分别与CD、CE交于点M、N , 有如下结论:①△ACE≌△DCB;②∠DPA=60°;③AC=DN;④EM=BN;⑤DC∥EB , 其中正确结论是(填序号)
18. 如图,△DAC和△EBC均是等边三角形,A、C、B三点共线,AE与BD相交于点P , AE与BD分别与CD、CE交于点M、N , 有如下结论:①△ACE≌△DCB;②∠DPA=60°;③AC=DN;④EM=BN;⑤DC∥EB , 其中正确结论是(填序号)
三、解答题
-
19. 计算:(1)、(-2x2)3+x2·x4(2)、(x-2)(x+2)-4(2x-1)20. 如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
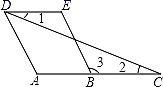
请完成解答过程:
解:∵AD∥BE(已知)
∠A=∠ ▲ ( ▲ )
又∵1=∠2(已知)
∴AC∥ ▲ ( ▲ )
∴∠3=∠ ▲ (两直线平行,内错角相等)
∴∠A=∠E( ▲ )
21. 如图所示,在 的正方形网格中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”. 是一个格点三角形,请你在图1,图2,图3中分别画出一个与 成轴对称的格点三角形,并将所画三角形涂上阴影.(注:所画的三个图不能重复.)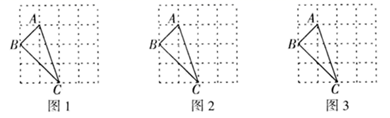 22. 某剧院的观众席的座位为扇形,且按下列方式设置:
22. 某剧院的观众席的座位为扇形,且按下列方式设置: (1)、按照上表所示的规律,当排数为6时,此时座位数为多少?(2)、写出座位数y与排数x之间的关系式;(3)、按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.23. 如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
(1)、按照上表所示的规律,当排数为6时,此时座位数为多少?(2)、写出座位数y与排数x之间的关系式;(3)、按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.23. 如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.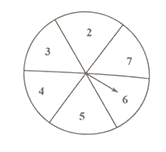
求:
(1)、转动转盘,转出的数字大于3的概率是多少?(2)、现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.①这三条线段能构成三角形的概率是.
②这三条线段能构成等腰三角形的概率是.
24. 小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程S(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题: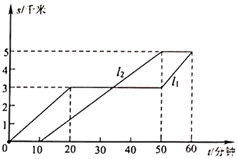 (1)、先出发,先出发了分钟;(答案直接填写到答题卡的横线上)(2)、求当t等于多少分钟时,小凡与小光在去图书馆的路上相遇;(3)、小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括停留的时间)25. 图1,是一个长为 ,宽为 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)、先出发,先出发了分钟;(答案直接填写到答题卡的横线上)(2)、求当t等于多少分钟时,小凡与小光在去图书馆的路上相遇;(3)、小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括停留的时间)25. 图1,是一个长为 ,宽为 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.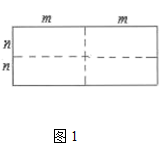
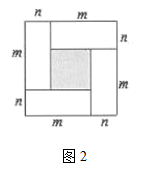
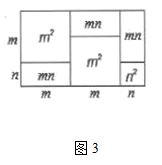 (1)、图2中的阴影部分的面积为;(2)、观察图2,三个代数式 , , 之间的等量关系是;(3)、若 , ,求 ;(4)、观察图3,你能得到怎样的代数恒等式呢?26. 如图,在△ABC中,AB=AC , 点D、E分别在AC及其延长线上,点B、F分别在AE两侧,连结CF , 已知AD=EC , BC=DF , BC∥DF .
(1)、图2中的阴影部分的面积为;(2)、观察图2,三个代数式 , , 之间的等量关系是;(3)、若 , ,求 ;(4)、观察图3,你能得到怎样的代数恒等式呢?26. 如图,在△ABC中,AB=AC , 点D、E分别在AC及其延长线上,点B、F分别在AE两侧,连结CF , 已知AD=EC , BC=DF , BC∥DF .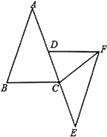 (1)、求证:△ABC≌△EFD;(2)、若CE=CF , FC平分∠DFE , 求∠A的度数.27. 如图1,在 中, 平分 , 平分 .
(1)、求证:△ABC≌△EFD;(2)、若CE=CF , FC平分∠DFE , 求∠A的度数.27. 如图1,在 中, 平分 , 平分 .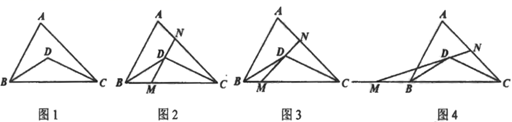 (1)、若 ,则 的度数为;(2)、若 ,直线 经过点 .
(1)、若 ,则 的度数为;(2)、若 ,直线 经过点 .①如图2,若 ,求 的度数(用含 的代数式表示);
②如图3,若 绕点 旋转,分别交线段 于点 ,试问在旋转过程中 的度数是否会发生改变?若不变,求出 的度数(用含 的代数式表示),若改变,请说明理由:
③如图4,继续旋转直线 ,与线段 交于点 ,与 的延长线交于点 ,请直接写出 与 的关系(用含 的代数式表示).