江西省赣州市经开区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-11 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列问题中,不适合用全面调查的是( )A、了解全班同学每周体育锻炼的时间 B、旅客上飞机前的安检 C、了解全县七年级学生的平均身高 D、学校招聘教师,对应聘人员面试3. 在实数3.14, , ,-5π,0.3030030003......, 中无理数有( )个A、1个 B、2个 C、3个 D、4个4. 已知关于x的不等式 的解集为 ,则 的取值范围是( )A、 B、 C、 D、5. 如下图,在下列条件中,能判定AB//CD的是( )
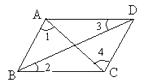 A、∠1=∠3 B、∠2=∠3 C、∠1=∠4 D、∠3=∠46. 在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )A、6,(﹣3,5) B、10,(3,﹣5) C、1,(3,4) D、3,(3,2)
A、∠1=∠3 B、∠2=∠3 C、∠1=∠4 D、∠3=∠46. 在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )A、6,(﹣3,5) B、10,(3,﹣5) C、1,(3,4) D、3,(3,2)二、填空题
-
7. 编写一个二元一次方程组,它的解为 ,则此方程组为8. 若(m+1)x|m|<2 019是关于x的一元一次不等式,则m= .9. 为了了解某市八年级 名学生的体重情况,从中抽查了 名学生的体重进行统计分析,在这个问题中,样本是10. 根据图中数据求阴影部分的面积和为.
 11. 若 , ,则 = .12. 某班数学兴趣小组对不等式组 ,讨论得到以下结论:①若a=5,则不等式组的解集为3<x≤5;②若a=2,则不等式组无解;③若不等式组无解,则a的取值范围为a<3;④若不等式组只有两个整数解,则a的值可以为5.1,其中,正确的结论的序号是 .
11. 若 , ,则 = .12. 某班数学兴趣小组对不等式组 ,讨论得到以下结论:①若a=5,则不等式组的解集为3<x≤5;②若a=2,则不等式组无解;③若不等式组无解,则a的取值范围为a<3;④若不等式组只有两个整数解,则a的值可以为5.1,其中,正确的结论的序号是 .三、解答题
-
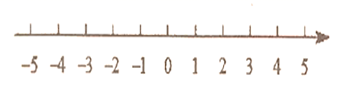
13. 计算:(1)、(2)、解方程:14. 解不等式组 ,并在数轴上表示解集.
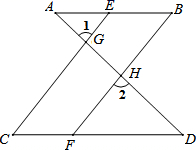
 15. 完成下面推理过程:
15. 完成下面推理过程:如图,已知 ,可推得
理由如下:
(已知),
且 ( ▲ ),
(等量代换).
( ▲ ).
▲
又 (已知),
▲ (等量代换).
( ▲ ).
16.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
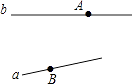 (1)、从火车站到码头怎样走最近,画图并说明理由;(2)、从码头到铁路怎样走最近,画图并说明理由;(3)、从火车站到河流怎样走最近,画图并说明理由.17. 如图,在直角坐标平面内,点A的坐标是 ,点B的坐标是
(1)、从火车站到码头怎样走最近,画图并说明理由;(2)、从码头到铁路怎样走最近,画图并说明理由;(3)、从火车站到河流怎样走最近,画图并说明理由.17. 如图,在直角坐标平面内,点A的坐标是 ,点B的坐标是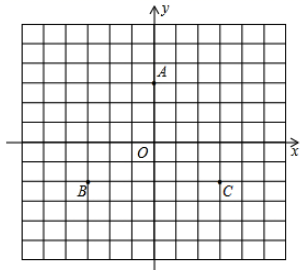 (1)、图中点C关于x轴对称的点D的坐标是 .(2)、如果将点B沿着与x轴平行的方向向右平移3个单位得到点 ,那么 、 两点之间的距离是 .(3)、求四边形ABCD的面积18. 如图,直线 相交于点 平分 平分
(1)、图中点C关于x轴对称的点D的坐标是 .(2)、如果将点B沿着与x轴平行的方向向右平移3个单位得到点 ,那么 、 两点之间的距离是 .(3)、求四边形ABCD的面积18. 如图,直线 相交于点 平分 平分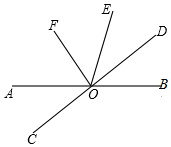 (1)、若 ,判断 与 的位置关系,并进行证明.(2)、若 求 的度数.19. 已知 的立方根是3, 的算术平方根是4,c是 的整数部分.(1)、求a,b,c的值;(2)、求 的平方根.20. 育人中学开展课外体育活动,决定开设 :篮球、 :乒乓球、 :踢毽子、 ;跑步四种活动项目.为了解学生最喜欢哪-种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
(1)、若 ,判断 与 的位置关系,并进行证明.(2)、若 求 的度数.19. 已知 的立方根是3, 的算术平方根是4,c是 的整数部分.(1)、求a,b,c的值;(2)、求 的平方根.20. 育人中学开展课外体育活动,决定开设 :篮球、 :乒乓球、 :踢毽子、 ;跑步四种活动项目.为了解学生最喜欢哪-种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.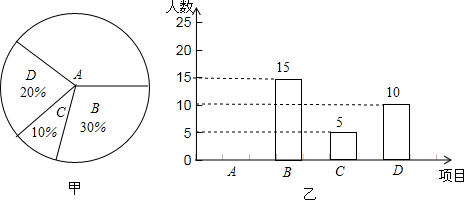 (1)、样本中最喜欢 项目的人数所占的百分比为 , 其所在扇形统计图中对应的圆心角度数是度;(2)、请求出样本中最喜欢 项目的人数是多少?请把条形统计图补充完整;(3)、若该校有学生 人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?21. 在我市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)、求每台电脑、每台电子白板各多少万元?(2)、根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,该校有几种购买方案?(3)、上面的哪种方案费用最低?按费用最低方案购买需要多少钱?22. 阅读材料:善于思考的小强同学在解方程组 时,采用了一 种“整体代换” 解法:
(1)、样本中最喜欢 项目的人数所占的百分比为 , 其所在扇形统计图中对应的圆心角度数是度;(2)、请求出样本中最喜欢 项目的人数是多少?请把条形统计图补充完整;(3)、若该校有学生 人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?21. 在我市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)、求每台电脑、每台电子白板各多少万元?(2)、根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,该校有几种购买方案?(3)、上面的哪种方案费用最低?按费用最低方案购买需要多少钱?22. 阅读材料:善于思考的小强同学在解方程组 时,采用了一 种“整体代换” 解法:解:将方程②变形: ,即 ③,把方程①代入③得: ,即
把 代入方程①,得 ,所以方程组的解为
请你解决以下问题
(1)、模仿小同学约“整体代换”法解方程组(2)、已知 满足方程组求 的值:
求出这个方程组的所有整数解.
23. 问题情境在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
 (1)、如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
(1)、如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;结论应用
(3)、如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于(用含α的式子表示).