福建省三明市建宁县2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-09-11 类型：期末考试

进入出卷网下载

一、单选题

1. 计算(a³)²的结果是（）

A、3a² B、2a³ C、a⁵ D、a⁶

查看试题解析
2. 如图，直线a，b被直线c所截.若a‖b，∠1 = 54°，则∠2的度数是（）

A、126° B、134° C、136° D、144°

查看试题解析
3. 生物学家发现了某种花粉的直径约为0.0000036毫米，数据0.0000036用科学记数法表示正确的是（）

A、3.6×10^﹣5 B、0.36×10^﹣5 C、3.6×10^﹣6 D、0.36×10^﹣6

查看试题解析
4. 下列事件中，是必然事件的是（）

A、任意买一张电影票，座位号是偶数 B、将油滴入水中，油会浮在水面上 C、车辆随机到达一个路口，遇到红灯 D、明天一定会下雨

查看试题解析
5. 如图所示的五角星是轴对称图形，它的对称轴共有（）

A、1条 B、3条 C、5条 D、无数条

查看试题解析
6. 在计算( $x + 2 y$ ) ( $- 2 y + x$ )时，最佳的方法是（）

A、运用多项式乘多项式法则 B、运用平方差公式 C、运用单项式乘多项式法则 D、运用完全平方公式

查看试题解析
7. 如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）

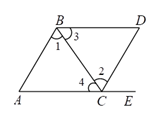A、∠3=∠4 B、∠1=∠2 C、∠D=∠DCE D、∠D+∠DCA=180°

查看试题解析
8. 已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）

A、1 B、2 C、8 D、11

查看试题解析
9. 在一个三角形中，若其中一个内角等于另两个内角的差，则（）

A、必有一个内角等于90° B、必有一个内角等于60° C、必有一个内角等于45° D、必有一个内角等于30°

查看试题解析
10. 计算 $(1^{3} + 2^{3} + \dots + 29^{3}) (2^{3} + 3^{3} + \dots + 30^{3})$ - $(2^{3} + 3^{3} + \dots + 29^{3}) (1^{3} + 2^{3} + \dots + 30^{3})$ 的结果是（）

A、2020 B、20200 C、2700 D、27000

查看试题解析

二、填空题

11. 计算 $x^{6} \cdot x^{2}$ 的结果是．

查看试题解析
12. 某林业部门统计某种幼树在一定条件下的移植成活率，结果如下表所示：
移植总数（n）
400
750
1500
3500
7000
9000
14000
成活数（m）
369
662
1335
3203
6335
8073
12628
成活的频率 $\frac{m}{n}$
0.923
0.883
0.890
0.915
0.905
0.897
0.902
根据表中数据，估计这种幼树移植成活率的概率为（精确到0.1）．

查看试题解析
13. 如图，AB//CD，且∠DEC = 100°，∠C = 45°，则∠B的度数是．

查看试题解析
14. 已知拖拉机油箱中有油50升，工作时每小时耗油6升，则油箱中的剩余油y (升)与工作时间x (小时)之间的关系式是．

查看试题解析
15. 在如图所示的2×2方格中，连接AB、AC，则∠1+∠2=度.

查看试题解析
16. 如图1所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按图2所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（图1）拼出来的图形的总长度是（结果用含 $a$ 、 $b$ 代数式表示）.

查看试题解析

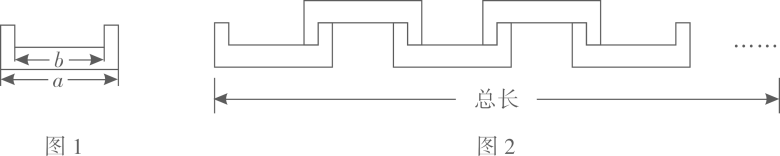
三、解答题

17. 计算：

(1)、 ${(- 2)}^{2} - 2020^{0} + 3^{- 2}$ ；

(2)、 $2 x^{3} y^{2} \cdot (- 9 x^{2}) \div (6 x^{4} y)$ ．

查看试题解析
18. 先化简，再求值： $x (x + 2) - {(x + 1)}^{2} + 7 x$ ，其中 $x = \frac{5}{7}$ ．

查看试题解析
19. 在一个不透明的布袋中，有六个完全相同的小球，把他们分别标号为1，2，2，3，4，5．李强从布袋中随机摸出一个小球．

(1)、求他摸出的小球标号是2的概率；

(2)、求他摸出的小球标号小于4的概率.

查看试题解析
20. 如图，已知ΔABC．

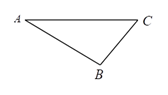(1)、在AC的上方作射线AE，使∠CAE =∠ACB（尺规作图，保留作图痕迹，不要求写作法）；

(2)、在(1)的条件下，在射线AE上取一点D，使AD=BC，连接CD，请说明∠ADC =∠B．

查看试题解析
21. 已知有理数x，y满足 $x + y = \frac{1}{2}$ ， $x y = - 3$ ．

(1)、求 $(x + 1) (y + 1)$ 的值；

(2)、求 $x^{2} + y^{2}$ 的值．

查看试题解析
22. 如图，在四边形ABCD中，AD‖BC，点E在AD 边上，BD平分∠EBC．

(1)、请说明∠1=∠2；

(2)、若AE=BE，请说明AB⊥BD．

查看试题解析
23. 某日上午8点，甲车从A地出发沿一条公路前往B地．行驶一段时间后，提高了速度，如图是甲车行驶路程s (千米)随行驶时间t (小时)变化的图象．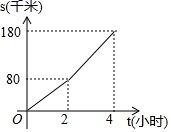

(1)、甲车提高速度前每小时行驶多少千米？

(2)、到上午11点时甲车行驶了多少千米？

(3)、同日上午9点，乙车也从A地出发沿同一条公路匀速前往B地．若在上午11点至12点之间(含11点和12点)能追上甲车，求乙车速度的取值范围．

查看试题解析
24. 已知ΔABC是等腰三角形．

(1)、若∠A=100°，求∠B的度数；

(2)、若∠A=70°，求∠B的度数；

(3)、若∠A= $α$ (45°< $α$ <90°)，过顶点B的角平分线BD与过顶点C的高CE交于点F，求∠BFC的度数(用含 $α$ 的式子表示)．

查看试题解析
25. 如图，四边形ABCD是长方形，E是边CD的中点，连接AE并延长交边BC的延长线于F，过点E作AF的垂线交边BC于M，连接AM．

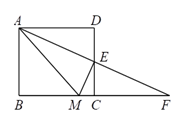(1)、请说明ΔADE≌ΔFCE；

(2)、试说明AM=BC+MC；

(3)、设S_△AEM= S₁ ， S_△ECM= S₂ ， S_△ABM= S₃ ，试探究S₁ ， S₂ ， S₃三者之间的等量关系，并说明理由．

查看试题解析

移植总数（n）	400	750	1500	3500	7000	9000	14000
成活数（m）	369	662	1335	3203	6335	8073	12628
成活的频率 $\frac{m}{n}$	0.923	0.883	0.890	0.915	0.905	0.897	0.902