福建省泉州石狮市2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-11 类型:期末考试
一、单选题
-
1. 下列 的值是方程 的解的是( )A、 B、 C、 D、2. 下列四组长度的小木棒中,按首尾顺次连结能组成一个三角形的是( )A、1,2,3 B、4,5,6 C、3,4,12 D、4,8,43. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 不等式组 的解集在数轴上表示为( )A、
4. 不等式组 的解集在数轴上表示为( )A、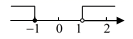 B、
B、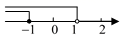 C、
C、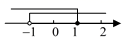 D、
D、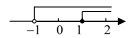 5. 下列正多边形地砖中,单独选用一种地砖不能铺满地面的是( )A、正三角形地砖 B、正方形地砖 C、正六边形地砖 D、正八边形地砖6. 我国元朝的数学著作《算学启蒙》记载:良马日行二百四十里,驽马日行一百五十里,两马同地出发,驽马先行一十二日,问良马几何追及之?其大意是:良马每天跑 里,驽马每天跑 里. 良马和驽马从同地出发,驽马先走 天,问良马追上驽马的时间为多少天?若设良马追上驽马的时间为
5. 下列正多边形地砖中,单独选用一种地砖不能铺满地面的是( )A、正三角形地砖 B、正方形地砖 C、正六边形地砖 D、正八边形地砖6. 我国元朝的数学著作《算学启蒙》记载:良马日行二百四十里,驽马日行一百五十里,两马同地出发,驽马先行一十二日,问良马几何追及之?其大意是:良马每天跑 里,驽马每天跑 里. 良马和驽马从同地出发,驽马先走 天,问良马追上驽马的时间为多少天?若设良马追上驽马的时间为 天,则可列方程为( ) A、 B、 C、 D、7. 如图,将一副直角三角板按如图所示叠放,其中 , , ,则 的大小是( )
天,则可列方程为( ) A、 B、 C、 D、7. 如图,将一副直角三角板按如图所示叠放,其中 , , ,则 的大小是( ) A、 B、 C、 D、8. 如图,将△ 绕点 顺时针旋转到△ 的位置,且点 恰好落在 边上,则下列结论不一定成立的是( )
A、 B、 C、 D、8. 如图,将△ 绕点 顺时针旋转到△ 的位置,且点 恰好落在 边上,则下列结论不一定成立的是( )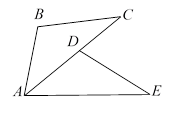 A、 B、 C、 ∥ D、 平分9. 在直角三角形 中, ∶ ∶ ∶ ∶ ,则 的值是( )A、 B、 C、 或 D、 或10. 某便利店分两次购进同款洗手液,第一次以每瓶 元的价格购进 瓶,第二次以每瓶 元的价格购进 瓶,并都以每瓶 元的价格全部卖出,结果发现赔了钱,则赔钱的原因是( )A、 B、 > C、 < D、与 , 的大小无关
A、 B、 C、 ∥ D、 平分9. 在直角三角形 中, ∶ ∶ ∶ ∶ ,则 的值是( )A、 B、 C、 或 D、 或10. 某便利店分两次购进同款洗手液,第一次以每瓶 元的价格购进 瓶,第二次以每瓶 元的价格购进 瓶,并都以每瓶 元的价格全部卖出,结果发现赔了钱,则赔钱的原因是( )A、 B、 > C、 < D、与 , 的大小无关二、填空题
-
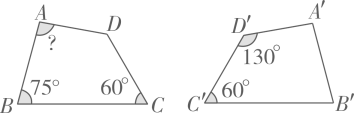
11. 已知方程2x+y=5,适用含x的代数式表示y,则y=.12. 若 > ,则 . (用“>”或“<”填空)13. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .14. 如图,四边形 ≌四边形 ,则 的大小是 .
 15. 如图,在 中, 是 边上的中线, , ,则 的周长为 .
15. 如图,在 中, 是 边上的中线, , ,则 的周长为 . 16. 如图,已知 的面积为 , . 现将 沿射线 方向平移a个单位到 的位置. 在平移过程中,若 所扫过部分的面积为 ,则a的值为 .
16. 如图,已知 的面积为 , . 现将 沿射线 方向平移a个单位到 的位置. 在平移过程中,若 所扫过部分的面积为 ,则a的值为 .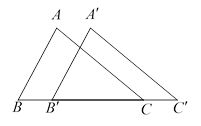
三、解答题
-
17. 解方程: .18. 解方程组:19. 解不等式: < ,并将解集在数轴上表示出来.
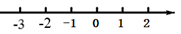 20. 如图,在△ 中, , ,点D是 边上的一点,将△ 沿 折叠,点C恰好落在BC边上的点E处.
20. 如图,在△ 中, , ,点D是 边上的一点,将△ 沿 折叠,点C恰好落在BC边上的点E处.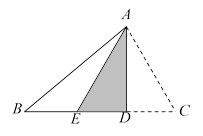 (1)、直接填空: 的大小是;(2)、求 的大小.21. 如图,已知△ 的三个顶点及点 、点 都在方格纸的格点上.
(1)、直接填空: 的大小是;(2)、求 的大小.21. 如图,已知△ 的三个顶点及点 、点 都在方格纸的格点上.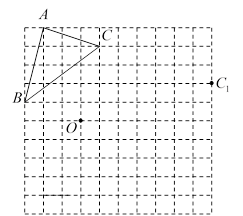 (1)、将△ 平移后得到△ ,点 是点 的对应点,请在图中补全△ ;(2)、画出△ ,使△ 和△ 关于点 成中心对称;(3)、上述△ 与△ 是否关于某点成中心对称?如果是,请写出该对称中心;如果不是,请说明理由.22. 某中学为丰富学生的校园生活,准备从某商店购买若干个同款足球和篮球,已知购买 个足球和 个篮球共需 元,购买 个足球比 个篮球要多花 元.(1)、求所购足球、篮球的单价各是多少元?(2)、若学校计划用不超过 元购买上述两种球共 个,问学校有哪几种购买方案?23. 如图,在△ 中, ,点 为△ 内部的一点. 连接OC,线段OC关于直线 对称的线段分别是 .
(1)、将△ 平移后得到△ ,点 是点 的对应点,请在图中补全△ ;(2)、画出△ ,使△ 和△ 关于点 成中心对称;(3)、上述△ 与△ 是否关于某点成中心对称?如果是,请写出该对称中心;如果不是,请说明理由.22. 某中学为丰富学生的校园生活,准备从某商店购买若干个同款足球和篮球,已知购买 个足球和 个篮球共需 元,购买 个足球比 个篮球要多花 元.(1)、求所购足球、篮球的单价各是多少元?(2)、若学校计划用不超过 元购买上述两种球共 个,问学校有哪几种购买方案?23. 如图,在△ 中, ,点 为△ 内部的一点. 连接OC,线段OC关于直线 对称的线段分别是 .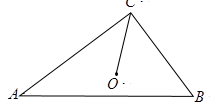 (1)、请借助三角尺在图中分别画出线段 ;(2)、试说明:点 三点在同一条直线上.
(1)、请借助三角尺在图中分别画出线段 ;(2)、试说明:点 三点在同一条直线上.