福建省宁德市2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-11 类型:期末考试
一、单选题
-
1. 下列图案分别表示“福”“禄”“寿”“喜”,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某种冠状病毒的直径是 0.00000012米.将数据 0.000 00012用科学记数法表示是( )A、0.12 ´10 B、0.12´10 C、1.2 ´10 D、1.2 ´103. 下列各图中,∠1与∠2是对顶角的是( )A、
2. 某种冠状病毒的直径是 0.00000012米.将数据 0.000 00012用科学记数法表示是( )A、0.12 ´10 B、0.12´10 C、1.2 ´10 D、1.2 ´103. 下列各图中,∠1与∠2是对顶角的是( )A、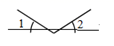 B、
B、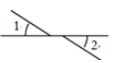 C、
C、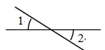 D、
D、 4. 掷一枚质地均匀硬币,前3次都是正面朝上,掷第4次时正面朝上的概率是( )A、0 B、 C、 D、15. 以下面各组数据为长度的三条线段,能组成三角形的是( )A、1,1,3 B、1,3,4 C、4,5,9 D、2,6,76. 下列运算正确的是( )A、4a -a =3a B、a ×a=a C、(3a) =6a D、a ¸a =a7. 如图,公园里有一座假山,要测假山两端A,B的距离,先在平地上取一个可直接到达 A 和B的点C,分别延长AC,BC到D,E,使CD=CA ,CE=CB,连接DE.这样就可利用三角形全等,通过量出DE的长得到假山两端A,B的距离.其中说明两个三角形全等的依据是( )
4. 掷一枚质地均匀硬币,前3次都是正面朝上,掷第4次时正面朝上的概率是( )A、0 B、 C、 D、15. 以下面各组数据为长度的三条线段,能组成三角形的是( )A、1,1,3 B、1,3,4 C、4,5,9 D、2,6,76. 下列运算正确的是( )A、4a -a =3a B、a ×a=a C、(3a) =6a D、a ¸a =a7. 如图,公园里有一座假山,要测假山两端A,B的距离,先在平地上取一个可直接到达 A 和B的点C,分别延长AC,BC到D,E,使CD=CA ,CE=CB,连接DE.这样就可利用三角形全等,通过量出DE的长得到假山两端A,B的距离.其中说明两个三角形全等的依据是( ) A、SSS B、ASA C、AAS D、SAS8. 在利用正六面体骰子进行频率估计概率的实验中,小颖同学统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A、SSS B、ASA C、AAS D、SAS8. 在利用正六面体骰子进行频率估计概率的实验中,小颖同学统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( ) A、朝上的点数是 5 的概率 B、朝上的点数是奇数的概率 C、朝上的点数是大于 2 的概率 D、朝上的点数是 3 的倍数的概率9. 根据如图所示的尺规作图痕迹判断,下列结论错误的是( )
A、朝上的点数是 5 的概率 B、朝上的点数是奇数的概率 C、朝上的点数是大于 2 的概率 D、朝上的点数是 3 的倍数的概率9. 根据如图所示的尺规作图痕迹判断,下列结论错误的是( )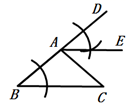 A、∠DAE=∠B B、∠C=∠EAC C、∠DAE=∠EAC D、AE∥BC10. 如图,点P在∠MAN的角平分线上,点B,C分别在AM,AN上,作PR⊥AM,PS⊥AN,垂足分别是R,S.若∠ABP+∠ACP=180°,则下面三个结论:①AS=AR;②PC∥AB;③△BRP≌△CSP.其中正确的是( )
A、∠DAE=∠B B、∠C=∠EAC C、∠DAE=∠EAC D、AE∥BC10. 如图,点P在∠MAN的角平分线上,点B,C分别在AM,AN上,作PR⊥AM,PS⊥AN,垂足分别是R,S.若∠ABP+∠ACP=180°,则下面三个结论:①AS=AR;②PC∥AB;③△BRP≌△CSP.其中正确的是( )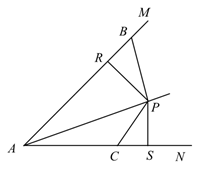 A、①② B、②③ C、①③ D、①②③
A、①② B、②③ C、①③ D、①②③二、填空题
-
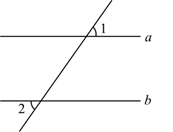
11. 若∠A=25°,则它的补角是°.12. 计算: .13. 如图,直线a∥b , 若∠1=41°,则∠2=°.
 14. 下列事件:①掷一枚质地均匀的硬币,正面朝上;②某彩票中奖率为 买100张一定会中奖;③13人中至少有2人的生日在同一个月.其中是必然事件的是(填序号).15. 如图,在△ABC 中,AC = AB , △ABC 的角平分线 AD交 BE 于点 F , 若∠AFE = 32° ,则∠FBD =°.
14. 下列事件:①掷一枚质地均匀的硬币,正面朝上;②某彩票中奖率为 买100张一定会中奖;③13人中至少有2人的生日在同一个月.其中是必然事件的是(填序号).15. 如图,在△ABC 中,AC = AB , △ABC 的角平分线 AD交 BE 于点 F , 若∠AFE = 32° ,则∠FBD =°.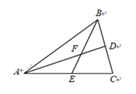 16. 有若干个形状大小完全相同的小长方形,现将其中 3 个如图 1 摆放,构造一个正方形;其中5 个如图 2 摆放,构造一个新的长方形(各小长方形之间不重叠且不留空隙).若图 1 和图2 中阴影部分的面积分别为 39 和 106,则每个小长方形的面积为 .
16. 有若干个形状大小完全相同的小长方形,现将其中 3 个如图 1 摆放,构造一个正方形;其中5 个如图 2 摆放,构造一个新的长方形(各小长方形之间不重叠且不留空隙).若图 1 和图2 中阴影部分的面积分别为 39 和 106,则每个小长方形的面积为 .
三、解答题
-
17. 计算:(1)、(x-1)(x+2)-x(x-2);(2)、(2ab -3a b+b)¸b +(a-b) ,其中a=2,b=-1.18. 请将下面的说理过程和理由补充完整.
如图,点B,E,C,F在一条直线上,BE=CF,AB∥DE,AB=DE,说明AC=DF.
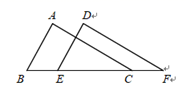
解:∵BE=CF,(已知)
∴BE+EC=CF+ ▲ . (等式的性质)
即 BC= ▲ .
∵AB∥DE,(已知)
∴∠B= ▲ . ( ▲ )
又∵AB=DE,(已知)
∴△ABC≌△DEF.( ▲ )
∴AC=DF.( ▲ )
19. 李大爷在如图1所示扇形湖畔的栈道上散步,他从圆心O出发,沿O→A→B→O 匀速运动,最后回到点O , 其中路径AB是一段长180米的圆弧.李大爷离出发点O的直线距离S(米)与运动时间t(分)之间的关系如图2所示.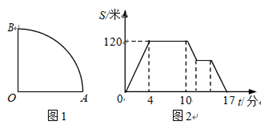 (1)、在时间段内,李大爷离出发点 O 的距离在增大;在 4~10 分这个时间段内,李大爷在路段上运动(填 OA , AB 或 OB);李大爷从点 O 出发到回到点 O 一共用了分钟;(2)、扇形栈道的半径是米,李大爷的速度为米/分;(3)、在与出发点 O 距离 75 米处有一个报刊亭,李大爷在该处买报纸时逗留了一会儿.已知李大爷在买报纸前后始终保持运动速度不变,则李大爷是在第分到达报刊亭,他在报刊亭停留了分钟.20. 为了缓解疫情对消费的冲击,某商场设置两种方案给顾客发放代金券,每位顾客均有一次获得代金券的机会.方案一:在一个装有 5 个红球、7 个黄球、8 个蓝球的不透明箱子中,每个球除颜色外都相同.从中任意摸出一个球,摸到红球获得代金券;方案二:在如图所示的长方形转盘 ABCD 中,AC , BD 交于点 O , OA = OB = OC = OD , △AOB 是等边三角形,任意转动指针 1 次,当指针停止转动时,指针指向区域①获得代金券.
(1)、在时间段内,李大爷离出发点 O 的距离在增大;在 4~10 分这个时间段内,李大爷在路段上运动(填 OA , AB 或 OB);李大爷从点 O 出发到回到点 O 一共用了分钟;(2)、扇形栈道的半径是米,李大爷的速度为米/分;(3)、在与出发点 O 距离 75 米处有一个报刊亭,李大爷在该处买报纸时逗留了一会儿.已知李大爷在买报纸前后始终保持运动速度不变,则李大爷是在第分到达报刊亭,他在报刊亭停留了分钟.20. 为了缓解疫情对消费的冲击,某商场设置两种方案给顾客发放代金券,每位顾客均有一次获得代金券的机会.方案一:在一个装有 5 个红球、7 个黄球、8 个蓝球的不透明箱子中,每个球除颜色外都相同.从中任意摸出一个球,摸到红球获得代金券;方案二:在如图所示的长方形转盘 ABCD 中,AC , BD 交于点 O , OA = OB = OC = OD , △AOB 是等边三角形,任意转动指针 1 次,当指针停止转动时,指针指向区域①获得代金券.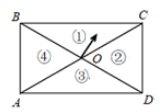 (1)、小明选择方案一,求他获得代金券的概率;(2)、你认为选择哪种方案更合算,并说明理由.21. 如图,已知△ABC,点P为BC上一点.
(1)、小明选择方案一,求他获得代金券的概率;(2)、你认为选择哪种方案更合算,并说明理由.21. 如图,已知△ABC,点P为BC上一点.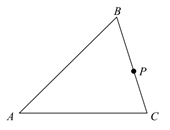 (1)、尺规作图:作直线EF,使得点A与点P关于直线EF对称,直线EF交直线AC于E,交直线AB于F;(保留作图痕迹,不写作法)(2)、连接PE,AP,AP交EF于点O,若AP平分∠BAC,请在(1)的基础上说明PE=AF.22. 生活处处有数学,比如在日历上就有许多数学规律.如图,是 2020 年 7 月份日历,我们任意选择一个如图所示的 X 形框,将同一斜线段两端的两个数相乘,再相减,例如:5 ´ 21 - 7 ´19 = -28,9 ´ 25 -11´ 23 = -28 ,不难发现,结果都是 -28 .
(1)、尺规作图:作直线EF,使得点A与点P关于直线EF对称,直线EF交直线AC于E,交直线AB于F;(保留作图痕迹,不写作法)(2)、连接PE,AP,AP交EF于点O,若AP平分∠BAC,请在(1)的基础上说明PE=AF.22. 生活处处有数学,比如在日历上就有许多数学规律.如图,是 2020 年 7 月份日历,我们任意选择一个如图所示的 X 形框,将同一斜线段两端的两个数相乘,再相减,例如:5 ´ 21 - 7 ´19 = -28,9 ´ 25 -11´ 23 = -28 ,不难发现,结果都是 -28 .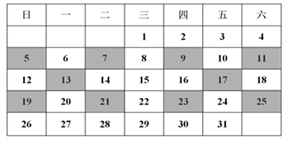 (1)、请你再选择一个X形框,参照例子写出算式,看看结果是否符合这个规律;(2)、若设X形框正中间的一个数为x , 请用整式的运算说明上述规律.23. 如图,已知等腰△ABC 中,AB=AC , ∠A<90°,CD 是△ABC 的高,BE 是△ABC 的角平分线,CD 与 BE 交于点 P . 当∠A 的大小变化时,△EPC 的形状也随之改变.
(1)、请你再选择一个X形框,参照例子写出算式,看看结果是否符合这个规律;(2)、若设X形框正中间的一个数为x , 请用整式的运算说明上述规律.23. 如图,已知等腰△ABC 中,AB=AC , ∠A<90°,CD 是△ABC 的高,BE 是△ABC 的角平分线,CD 与 BE 交于点 P . 当∠A 的大小变化时,△EPC 的形状也随之改变.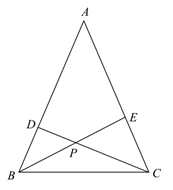 (1)、当∠A=44°时,求∠BPD 的度数;(2)、设∠A=x°,∠EPC=y°,求变量 y 与 x 的关系式;(3)、当△EPC 是等腰三角形时,请直接写出∠A 的度数.
(1)、当∠A=44°时,求∠BPD 的度数;(2)、设∠A=x°,∠EPC=y°,求变量 y 与 x 的关系式;(3)、当△EPC 是等腰三角形时,请直接写出∠A 的度数.