福建省福州市2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-11 类型:期末考试
一、单选题
-
1. 点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在实数 ,-3,-1,0中,最小的是( )A、 B、-3 C、-1 D、03. 2的算术平方根是( )A、2 B、±2 C、± D、4. 下列事件中,最适合采用普查的是( )A、对我校七年级一班学生出生日期的调查 B、对全国中学生节水意识的调查 C、对山东省初中学生每天阅读时间的调查 D、对某批次灯泡使用寿命的调查5. 如图所示,不等式的解集是( )
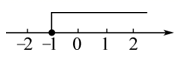 A、 B、 C、 D、6. 若 是方程 的一个解,则 的值是( )A、5 B、1 C、-5 D、-17. 如图,在三角形 中,若 , 于点 ,则下列线段的长度可以表示为点 到直线 距离的是( )
A、 B、 C、 D、6. 若 是方程 的一个解,则 的值是( )A、5 B、1 C、-5 D、-17. 如图,在三角形 中,若 , 于点 ,则下列线段的长度可以表示为点 到直线 距离的是( ) A、 B、 C、 D、8. 如图,下列选项中,不能判断直线 的是( )
A、 B、 C、 D、8. 如图,下列选项中,不能判断直线 的是( ) A、 B、 C、 D、9. 已知 ,下列不等式一定成立的是( )A、 B、 C、 D、10. 在平面直角坐标系中, , ,其中 ,则下列对 长度判断正确的是( )A、 B、 C、 D、无法确定
A、 B、 C、 D、9. 已知 ,下列不等式一定成立的是( )A、 B、 C、 D、10. 在平面直角坐标系中, , ,其中 ,则下列对 长度判断正确的是( )A、 B、 C、 D、无法确定二、填空题
-
11. 计算: .12. 在一次立定跳远测试中,10名学生所测的成绩(单位:厘米)如下:182,160,169,178,180,158,156,163,161,150,则这一组数据中最大值与最小值的差是 .13. 二元一次方程 的正整数解共有个.14. 《九章算术》是我国东汉年间编订的一部数学经典著作,其中有一个问题是:“今有三人公车,二车空;二人公车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,若每3人坐一辆车,则有2辆空车;若每2人坐一辆车,则有9人需要步行,问人与车各多少?设共有 人, 辆车,则可列方程组为 .15. 如图,将长方形分成四个区域,其中 , 两正方形区域的面积分别是1和6,则剩余区域的面积是 .
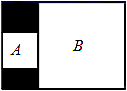 16. 如图,已知 ,点 在两平行线之间,连接 , , 的平分线与 的平分线的反向延长线交于点 ,若 ,则 的度数是 .
16. 如图,已知 ,点 在两平行线之间,连接 , , 的平分线与 的平分线的反向延长线交于点 ,若 ,则 的度数是 .
三、解答题
-
17. 计算: .18. 解方程组:19. 请补全证明过程及推理依据.已知:如图,点 , , 分别是三角形 的边 , , 上的点,若 , .求证: .
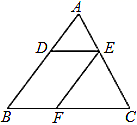
证明:∵ ,
∴ ▲ .( ▲ )
∵ ,
∴ ,( ▲ )
∴ ,( ▲ )
∴ .
20. 已知足球场的形状是一个长方形,而国际标准球场的长度 和宽度 (单位:米)的取值范围分别是 , .若某球场的宽与长的比是1:1.5,面积为7350平方米,请判断该球场是否符合国际标准球场的长宽标准,并说明理由.21. 2020年是决胜全面建成小康社会,决战脱贫攻坚之年.贫困地区的小康建成是最艰巨最繁重的任务.国务院扶贫开发领导小组指出贫困户脱贫人均年收入要达到4000元,根据某贫困县随机抽取的2019年居民人均年收入统计情况,绘制了如下的频数分布表:收入(元)
频数(人数)
频率
80
0.01
0.45
0.3
800
0.1
合计
1
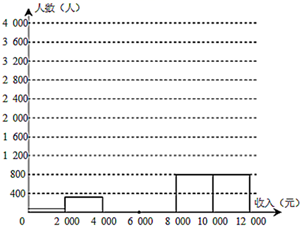 (1)、填空:m= , p=;(2)、请补全频数分布直方图;(3)、若该县共有6万居民,试估计仍未脱贫的居民人数.22. 如图,在平面直角坐标系中, , ,连接 交 轴于点 ,连接 .
(1)、填空:m= , p=;(2)、请补全频数分布直方图;(3)、若该县共有6万居民,试估计仍未脱贫的居民人数.22. 如图,在平面直角坐标系中, , ,连接 交 轴于点 ,连接 . (1)、求三角形 的面积;(2)、求点 的坐标.23. 2台大收割机和5台小收割机同时工作2天共收割小麦3.6公顷,3台大收割机和2台小收割机同时工作5天共收割小麦8公顷.(1)、求1台大收割机和1台小收割机每天各收割小麦多少公顷?(2)、已知大收割机每台租金600元/天,小收割机每台租金120元/天,某农场准备租用两种收割机共15台,且大收割机的数量不少于小收割机的一半,若每天总租金不超过5000元,设租赁大收割机 台,求该农场的租赁方案?24. 如图,在四边形 中, ,对角线 与 相交于点 ,且 .
(1)、求三角形 的面积;(2)、求点 的坐标.23. 2台大收割机和5台小收割机同时工作2天共收割小麦3.6公顷,3台大收割机和2台小收割机同时工作5天共收割小麦8公顷.(1)、求1台大收割机和1台小收割机每天各收割小麦多少公顷?(2)、已知大收割机每台租金600元/天,小收割机每台租金120元/天,某农场准备租用两种收割机共15台,且大收割机的数量不少于小收割机的一半,若每天总租金不超过5000元,设租赁大收割机 台,求该农场的租赁方案?24. 如图,在四边形 中, ,对角线 与 相交于点 ,且 . (1)、求证: 平分 ;(2)、若 ,且 , 平分 交 边于点 ,求 的值.25. 如图,在平面直角坐标系 中,点 , 分别是第三象限与第二象限内的点,将 , 两点先向右平移 个单位,再向下平移1个单位得到 , 两点(点 对应点 ).
(1)、求证: 平分 ;(2)、若 ,且 , 平分 交 边于点 ,求 的值.25. 如图,在平面直角坐标系 中,点 , 分别是第三象限与第二象限内的点,将 , 两点先向右平移 个单位,再向下平移1个单位得到 , 两点(点 对应点 ). (1)、写出 , 两点的坐标;(用含相关字母的代数式表示)(2)、连接 ,过点 作 的垂线 , 是直线 上一点,连接 ,且 的最小值为1.
(1)、写出 , 两点的坐标;(用含相关字母的代数式表示)(2)、连接 ,过点 作 的垂线 , 是直线 上一点,连接 ,且 的最小值为1.①若 ,求证:直线 轴;
②在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,这条直线上有无数个点,每一个点的坐标 都是这个方程的一个解.在①的条件下,若关于 , 的二元一次方程 ( )的图象经过点 , 及点 ,判断 与 是否相等,并说明理由.