江苏省徐州市2020年数学中考模拟试卷(二)
试卷更新日期:2020-09-11 类型:中考模拟
一、单选题。
-
1. 2020的倒数是( )A、 B、 C、2020 D、-20202. 下列计算正确的是( )A、 B、 C、 D、3. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、84. 使二次根式 有意义的x的取值范围是( )A、 B、 C、 D、5. 如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现在用一把剪刀沿着它的 棱剪开成一个平面图形,则展开图可以是( )
 A、
A、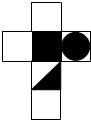 B、
B、 C、
C、 D、
D、 6. 一组数据:1,3,3,5,若添加一个数据3,则下列统计量中发生变化的是( )A、平均数 B、中位数 C、众数 D、方差7. 已知菱形 是动点,边长为4, ,若 ,则 ( )
6. 一组数据:1,3,3,5,若添加一个数据3,则下列统计量中发生变化的是( )A、平均数 B、中位数 C、众数 D、方差7. 已知菱形 是动点,边长为4, ,若 ,则 ( ) A、 B、4 C、 D、18. 如图,抛物线 ( 是常数, )与x轴交于A,B两点,顶点 给出下列结论:① ;②若 在抛物线上,则 ;③关于x的方程 有实数解,则 ;④当 时, 为等腰直角三角形,其中正确的结论是( )
A、 B、4 C、 D、18. 如图,抛物线 ( 是常数, )与x轴交于A,B两点,顶点 给出下列结论:① ;②若 在抛物线上,则 ;③关于x的方程 有实数解,则 ;④当 时, 为等腰直角三角形,其中正确的结论是( )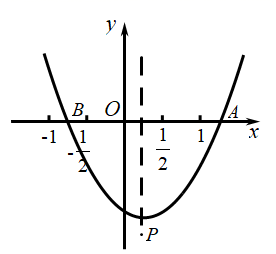 A、①② B、①③ C、②③ D、②④
A、①② B、①③ C、②③ D、②④二、填空题。
-
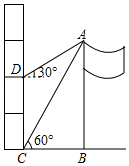
9. 因式分解: =.10. 1米=10亿纳米,某新型冠状病毒直径约为90纳米,90纳米用科学记数法可表示为米.11. 已知 ,是方程组 的解,则 的值是.12. 如果关于 的一元二次方程 有一个根是2 ,那么另一个根是.13. 点 和 的连线垂直于 轴,则 的值为.14. 若一个正多边形的外角与它的内角相等,则这个多边形为.15. 已知圆锥的母线长为6cm,侧面展开图是半圆,则圆锥的底面圆半径为 .16. 如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上.已CD=9.6m知,则旗杆AB的高度为m.
 17. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线解析式为.18. 如图,在矩形ABCD中, ,点E在AD边上,且 ,动点P从点A出发,沿AB运动到点B停止,过点E作 ,交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为.
17. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线解析式为.18. 如图,在矩形ABCD中, ,点E在AD边上,且 ,动点P从点A出发,沿AB运动到点B停止,过点E作 ,交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为.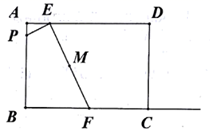
三、解答题
-
19. 如下:(1)、计算:(2)、化简:20. 如下:(1)、解方程:(2)、解不等式组:21. 为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.(1)、直接写出甲投放的垃圾恰好是A类的概率;(2)、求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.22. 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.

 (1)、频数分布表中 的值: , ;(2)、补全频数分布直方图;(3)、若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?23. 如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在AB上,且BF=DE.
(1)、频数分布表中 的值: , ;(2)、补全频数分布直方图;(3)、若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?23. 如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在AB上,且BF=DE. (1)、求证:四边形BDEF是平行四边形;(2)、线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论.24. 如图, 是 的直径, 切 于点A , 切 于点B , 且 .
(1)、求证:四边形BDEF是平行四边形;(2)、线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论.24. 如图, 是 的直径, 切 于点A , 切 于点B , 且 .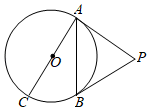 (1)、求 的度数;(2)、若 ,求点O到弦 的距离.25. 某工厂为贯彻落实“绿水青山就是金山银山“的发展理念,投资组建了日废水处理量为m吨的废水处理车间,对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大,该车间经常无法完成当天工业废水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水,每天需固定成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.(1)、求该车间的日废水处理量m;(2)、为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过10元/吨,试计算该厂一天产生的工业废水量的范围.26. 定义:
(1)、求 的度数;(2)、若 ,求点O到弦 的距离.25. 某工厂为贯彻落实“绿水青山就是金山银山“的发展理念,投资组建了日废水处理量为m吨的废水处理车间,对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大,该车间经常无法完成当天工业废水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水,每天需固定成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.(1)、求该车间的日废水处理量m;(2)、为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过10元/吨,试计算该厂一天产生的工业废水量的范围.26. 定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
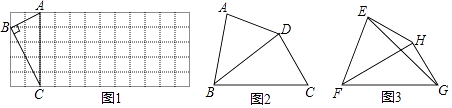 (1)、如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);(2)、如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
(1)、如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);(2)、如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”;
(3)、如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2 ,求FH的长.27. 如图,直线 与 , 轴分别交于点 , ,与反比例函数 图象交于点 , ,过点 作 轴的垂线交该反比例函数图象于点 . (1)、求点 的坐标.(2)、若 .
(1)、求点 的坐标.(2)、若 .①求 的值.
②试判断点 与点 是否关于原点 成中心对称?并说明理由.
28. 如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1. (1)、求抛物线L的解析式;(2)、将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;(3)、设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
(1)、求抛物线L的解析式;(2)、将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;(3)、设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.