江苏省南通市如皋市、崇川区2020年数学中考一模试卷

试卷更新日期：2020-09-11 类型：中考模拟

进入出卷网下载

一、单选题。

1. 如果温度上升10℃记作+10℃，那么温度下降5℃记作（）

A、+10℃ B、﹣10℃ C、+5℃ D、﹣5℃

查看试题解析
2. 据报道，国庆70周年阅兵是进入新时代的首次国庆阅兵，是共和国武装力量全面重塑后的首次整体亮相，阅兵编59个方(梯)队和联合军乐团，总规模约1.5万人，各型飞机160余架、装备580台套，是近几次阅兵中规模最大的一次.将1.5万人用科学记数法表示为（）

A、150×10²人 B、15×10³人 C、1.5×10⁴人 D、0.15×10⁵人

查看试题解析
3. 如图是由5个完全相同的小正方形搭成的几何体，如果将小正方体A放到小正方体B的正上方，则它的（）

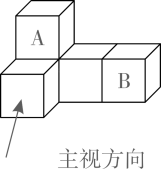A、主视图会发生改变 B、俯视图会发生改变 C、左视图会发生改变 D、三种视图都会发生改变

查看试题解析
4.
如图，△ABC沿着由点B到点E的方向，平移到△DEF，已知BC=5．EC=3，那么平移的距离为（　　）

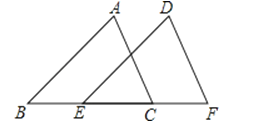A、2 B、3 C、5 D、7

查看试题解析
5. 如图，一辆小车沿倾斜角为α的斜坡向上行驶13m，若sinα $= \frac{5}{13}$ ，则小车上升的高度是（）

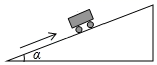A、5m B、6m C、6.5m D、12m

查看试题解析
6. 在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的( )

A、众数 B、方差 C、平均数 D、中位数

查看试题解析
7. 如图，AB是⊙O的直径，O是圆心，弦CD⊥AB于E，AB=10，CD=8，则OE的长为（）

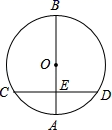A、2 B、3 C、4 D、5

查看试题解析
8. 已知方程x²﹣3x+1=0的两个根分别是x₁ ， x₂ ，则x₁²x₂+x₁x₂²的值为（）

A、﹣6 B、﹣3 C、3 D、6

查看试题解析
9. 一个有进水管和出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内即进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（L）与时间x（min）之间的关系如图所示，则每分钟的出水量为（　　）

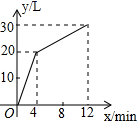A、5L B、3.75L C、2.5L D、1.25L

查看试题解析
10. 如图，矩形ABCD中，AB=2，AD=3.E，F分别是AD，CD上的动点，EF=2.Q是EF的中点，P为BC上的动点，连接AP，PQ.则AP+PQ的最小值等于（）

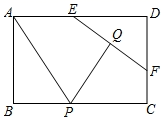A、2 B、3 C、4 D、5

查看试题解析

二、填空题。

11. 计算3²﹣( $\sqrt{5} +$ 1)⁰=.

查看试题解析
12. 函数y= $\sqrt{x - 2}$ 中，自变量x的取值范围是；实数2﹣ $\sqrt{3}$ 的倒数是．

查看试题解析
13. 一个n边形的每个外角都等于36°，则n=.

查看试题解析
14. 因式分解：a²﹣9b²＝.

查看试题解析
15. 已知a²+5ab+b²=0（a≠0，b≠0），则代数式 $\frac{b}{a}$ + $\frac{a}{b}$ 的值等于．

查看试题解析
16. 75°的圆心角所对的弧长是 $2.5 π$ cm，则此弧所在圆的半径是cm．

查看试题解析
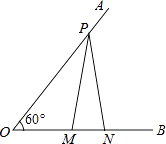
17. 如图，已知∠AOB=60°，点P在边OA上，OP=12，点M，N在边OB上，PM=PN，若MN=2，则OM= ．

查看试题解析
18. 当 $0 \leq x \leq 3$ 时，直线 $y = a$ 与抛物线 $y = {(x ﹣ 1)}^{2} ﹣ 3$ 有交点，则a的取值范围是．

查看试题解析

三、解答题

19. 如下：

(1)、解不等式组 ${\begin{array}{l} 3 x - 6 \geq x - 4 \\ 2 x + 1 > 3 (x - 1) \end{array}$ 并写出它的所有整数解.

(2)、先化简，再求值：(2x+1)²﹣2(x﹣1)(x+3)﹣2，其中x $= \sqrt{2}$ .

查看试题解析
20. 如图，要测量池塘两岸相对的两点A，B的距离，可以在池塘外取AB的垂线BF上的两点C，D，使BC=CD，再画出BF的垂线DE，使E与A，C在一条直线上，这时测得DE的长就是AB的长。为什么？

查看试题解析
21. 某商店在某一时间以每件60元的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%，卖这两件衣服总的是盈利还是亏本，还是不盈不亏？

查看试题解析
22. 某商场举办抽奖活动，规则如下：在不透明的袋子中有2个黑球和2个红球，这些球除颜色外都相同.顾客每次摸出一个球，若摸到黑球，则获得1份奖品；若摸到红球，则没有奖品.

(1)、如果小芳只有一次摸球机会，那么小芳获得奖品的概率为；

(2)、如果小芳有两次摸球机会(摸出后不放回)，求小芳获得2份奖品的概率.

查看试题解析
23. 某校为了解七、八年级学生一分钟跳绳情况，从这两个年级随机抽取 $50$ 名学生进行测试，并对测试成绩（一分钟跳绳次数）进行整理、描述和分析，下面给出了部分信息：
七年级学生一分钟跳绳成绩频数分布直方图

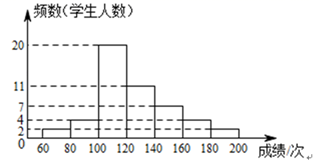
七，八年级学生一分钟跳绳成绩分析表

七年级学生一分钟跳绳成绩（数据分7组： $60 \leq x < 80 ， 80 \leq x < 100 ， \dots ， 180 \leq x < 200$ ）在 $100 \leq x < 120$ 这一组的是：

100 101 102 103 105 106 108 109 109 110 110 111 112 113 115 115 115 116 117 119

根据以上信息，回答下列问题：

(1)、表中 $a =$ ；

(2)、在这次测试中，七年级甲同学的成绩122次，八年级乙同学的成绩125，他们的测试成绩，在各自年级所抽取的50名同学中，排名更靠前的是（填“甲”或“乙”），理由是.

(3)、该校七年级共有500名学生，估计一分钟跳绳不低于116次的有多少人？

查看试题解析
24. 如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径.

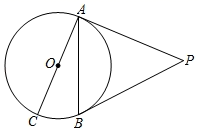(1)、若∠BAC=25°，求∠P的度数；

(2)、若∠P=60°，PA=2 $\sqrt{3}$ ，求AC的长.

查看试题解析
25. 已知抛物线y=﹣x²+2bx+1﹣2b(b为常数).

(1)、若点(2，5)在该抛物线上，求b的值；

(2)、若该抛物线的顶点坐标是(m，n)，求n关于m的函数解析式；

(3)、若抛物线与x轴交点之间的距离大于4，求b的取值范围.

查看试题解析
26. 如图，△ABC中，P'是边AB上一点，四边形P'Q'M'N'是正方形，点Q'， $M^{'}$ 在边BC上，点N'在△ABC内.连接BN'，并延长交AC于点N，NM⊥BC于点M，NP⊥MN交AB于点P，PQ⊥BC于点Q.

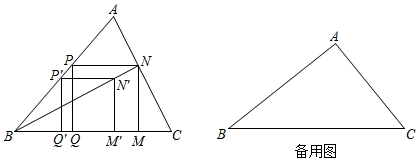(1)、求证：四边形PQMN为正方形；

(2)、若∠A=90°，AC=1.5m，△ABC的面积=1.5m².求PN的长.

查看试题解析
27. 定义：对于函数y，我们称函数叫做函数|y|的正值函数.例如：函数y $= \frac{1}{x}$ 的正值函数为y=| $\frac{1}{x}$ |.如图，曲线y $= \frac{4}{x}$ (x＞0)请你在图中画出y=x+3的正值函数的图象.

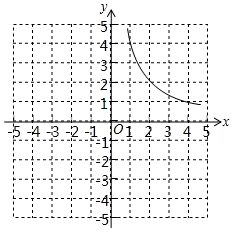(1)、写出y=x+3的正值函数的两条性质；

(2)、y=x+3的正值函数的图象与x轴、y轴、曲线y $= \frac{4}{x}$ (x＞0)的交点分别是A，B，C.点D是线段AC上一动点(不包括端点)，过点D作x轴的平行线，与正值函数图象交于另一点E，与曲线交于点P.
①试求△PAD的面积的最大值；

②探索：在点D运动的过程中，四边形PAEC能否为平行四边形？若能，求出此时点D的坐标；若不能，请说明理由.

查看试题解析