江苏省南京市鼓楼区2020年数学中考一模试卷

试卷更新日期：2020-09-11 类型：中考模拟

进入出卷网下载

一、单选题。

1. “鼓楼e学校一停课不停学在线课堂”在此次疫情期间为全国师生提供鼓楼教育的“云服务”，课程日均访问量达1200000，用科学记数法表示1200000是（）

A、0.12×10⁶ B、1.2×10⁷ C、1.2×10⁶ D、12×10⁵

查看试题解析
2. $\sqrt{4}$ 表示4的（）

A、平方 B、平方根 C、算术平方根 D、立方根

查看试题解析
3. 数轴上，点A，B分别表示﹣1、7，则线段AB的中点C表示的数是（）

A、2 B、3 C、4 D、5

查看试题解析
4. 已知5≤ $\sqrt{a}$ ≤7，4≤ $\sqrt{b}$ ≤6，则 $\sqrt{a + b}$ 的整数部分可以是（）

A、9 B、10 C、11 D、12

查看试题解析
5. 某班37名同学中只有1位同学身高是165cm.若除甲、乙外其余35名同学身高的平均数和中位数都是165cm，则该班37名同学身高的平均数a和中位数b（单位：cm），不可能是（）

A、a＞165，b＝165 B、a＜165，b＝165 C、a＜165，b＝164 D、a＝165，b＝166

查看试题解析
6. 如图，A，B两地相距am，它们之间有一半径为r的圆形绿地（r＜ $\frac{a}{2}$ ），绿地圆心位于AB连线的中点O处，分别过A、B作⊙O的切线相交于C，切点分别为D、E.现规划两条驾车路径：①B→E→C→D→A；②B→E→（沿 $\overset{⌢}{E D}$ ）→D→A，则下列说法正确的是（）

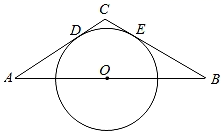A、①较长 B、②较长 C、①②一样长 D、以上皆有可能

查看试题解析

二、填空题。

7. 写出一个数，使这个数等于它的倒数：.

查看试题解析
8. 若代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是。

查看试题解析
9. 计算 $\frac{3}{\sqrt{2}} + \sqrt{\frac{1}{2}}$ 的结果是.

查看试题解析
10. 解方程 $\frac{2}{x - 3}$ ＝ $\frac{3}{x}$ 得.

查看试题解析
11. 已知方程2x²+4x﹣3＝0的两根分别为x₁、x₂ ，则x₁+x₂＝， x₁x₂＝.

查看试题解析
12. 一组数据2，3，2，3，5的方差是.

查看试题解析
13. 若正比例函数y＝k₁x的图象与反比例函数y＝ $\frac{k_{2}}{x}$ 的图象都经过点(2，3)，则k₁x＝ $\frac{k_{2}}{x}$ 的解是.

查看试题解析
14. 如图，点O是正五边形ABCDE的中心，连接BD、OD，则∠BDO＝°.

查看试题解析
15. 如图，BC是⊙O的切线，D是切点.连接BO并延长，交⊙O于点E、A，过A作AC⊥BC，垂足为C.若BD＝8，BE＝4，则AC＝.

查看试题解析
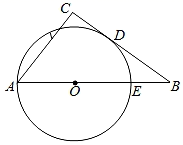16. 用若干个相同的小正方体搭一个几何体，该几何体的主视图、俯视图如图所示.若小正方体的棱长为1，则搭成的几何体的表面积是.

查看试题解析

三、解答题

17. 计算 $\frac{a}{a - 1} + \frac{3 a - 1}{1 - a^{2}}$ .

查看试题解析
18.

(1)、解不等式5x+2≥3（x﹣1），并把它的解集在数轴上表示出来.

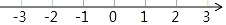(2)、写出一个实数k，使得不等式x＜k和（1）中的不等式组成的不等式组恰有3个整数解.

查看试题解析
19. 如图，已知AB∥CD，直线EF分别交直线AB、CD于点G、H，GI、HI分别平分∠BGH、∠GHD.

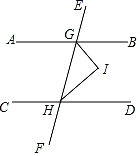(1)、求证GI⊥HI.

(2)、请用文字概括（1）所证明的命题：.

查看试题解析
20. 如图是某区1500名小学生和初中生的视力情况和他们每节课课间户外活动平均时长的统计图.

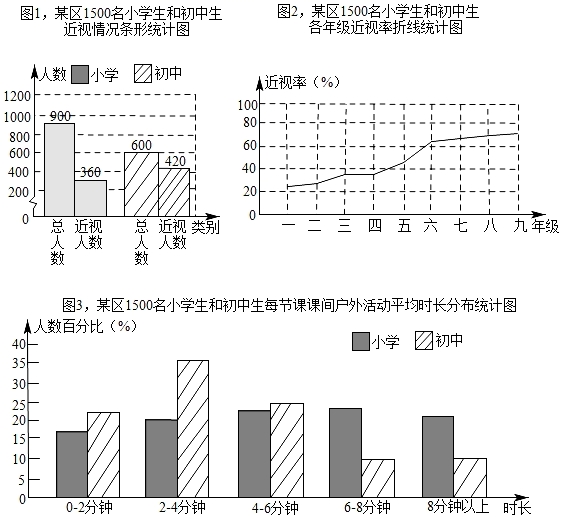(1)、根据图1，计算该区1500名学生的近视率；

(2)、根据图2，从两个不同的角度描述该区1500名学生各年级近视率的变化趋势；

(3)、根据图1、图2、图3，描述该区1500名学生近视率和所在学段（小学、初中）、每节课课间户外活动平均时长的关系.

查看试题解析
21. 如下：

(1)、不透明的袋子A中装有红球1个、白球1个，不透明的袋子B中装有红球1个、白球2个，这些球除颜色外无其他差别.分别从两个袋子中随机摸出一个球，求摸出的两个球颜色不同的概率；

(2)、甲、乙两人解同一道数学题，甲正确的概率为 $\frac{1}{3}$ ，乙正确的概率为 $\frac{1}{4}$ ，则甲乙恰有一人正确的概率是.

查看试题解析
22. 点E、F分别是菱形ABCD边BC、CD上的点.

(1)、如图，若CE＝CF，求证AE＝AF；

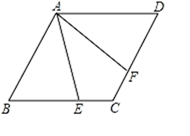(2)、判断命题“若AE＝AF，则CE＝CF”的真假.若真，请证明；若假，请在备用图上画出反例.

查看试题解析

23. 某工厂生产A、B、C三种产品，这三种产品的生产数量均为x件.它们的单件成本和固定成本如表：

产品	单件成本（元/件）	固定成本（元）
A	0.1	1100
B	0.8	a
C	b（b＞0）	200

（注：总成本＝单件成本×生产数量+固定成本）

(1)、若产品A的总成本为y_A ，则y_A关于x的函数表达式为.

(2)、当x＝1000时，产品A、B的总成本相同.

①求a；

②当x≤2000时，产品C的总成本最低，求b的取值范围.

查看试题解析

24. 如图， $△ A B C$ 内接于⊙O，∠BAC＝45°，AD⊥BC，垂足为D，BD＝6，DC＝4.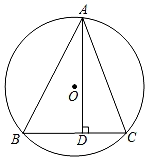

(1)、求⊙O的半径；

(2)、求AD的长.

查看试题解析
25. 如图，用一个平面去截正方体ABCDEFGH，得到了三棱锥S﹣DPQ.若∠SPD＝45°，∠SQD＝37°，PQ＝1，求SD的长.（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75.）

查看试题解析
26. 已知y是x的二次函数，该函数的图象经过点A(0，5)、B(1，2)、C(3，2).

(1)、求该二次函数的表达式，画出它的大致图象并标注顶点及其坐标；

(2)、结合图象，回答下列问题：
①当1≤x≤4时，y的取值范围是；

②当m≤x≤m+3时，求y的最大值（用含m的代数式表示）；

③是否存在实数m、n（m≠n），使得当m≤x≤n时，m≤y≤n？若存在，请求出m、n；若不存在，请说明理由.

查看试题解析

27. 如图，已知矩形纸片ABCD，怎样折叠，能使边AB被三等分？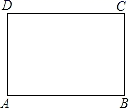

以下是小红的研究过程.

思考过程

要使边AB被三等分，若从边DC上考虑，就是要折出DM＝ $\frac{1}{3}$ DC，

也就是要折出DM＝ $\frac{1}{3}$ AB，

当DB、AM相交于F时，即要折出对角线上的DF＝ $\frac{1}{4}$ DB.那么…

折叠方法和示意图

①折出DB；对折纸片，使D、B重合，得到的折痕与DB相交于点E；继续折叠纸片，使D、B与E重合，得到的折痕与DB分别相交于点F、G；

②折出AF、CG，分别交边CD、AB于M、Q；

③过M折纸片，使D落在MC上，得到折痕MN，则边AB被N、Q三等分.

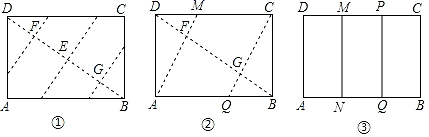(1)、整理小红的研究过程，说明AN＝NQ＝QB；

(2)、用一种与小红不同的方法折叠，使边AB被三等分.（需简述折叠方法并画出示意图）

查看试题解析