江苏省靖江市2020年数学中考适应性试卷
试卷更新日期:2020-09-11 类型:中考模拟
一、单选题。
-
1. 在0,1,﹣3,|﹣3|这四个数中,最小的数是( )A、0 B、1 C、﹣3 D、|﹣3|2. 如图是由5个相同的小立方体搭成的一个几何体,从左面看这个几何体,看到的形状图是( )
 A、
A、 B、
B、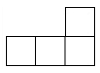 C、
C、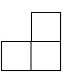 D、
D、 3. 在期末体育考核中,成绩分为优秀、合格、不合格三个档次,某班有40名学生,达到优秀的有18人,合格的有17人,则这次体育考核中,不合格人数的频率是( )A、0.125 B、0.45 C、0.425 D、1.254. 若方程x2+3x+c=0有实数根,则c的取值范围是( )A、c≤ B、c≤ C、c≥ D、c≥5. 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
3. 在期末体育考核中,成绩分为优秀、合格、不合格三个档次,某班有40名学生,达到优秀的有18人,合格的有17人,则这次体育考核中,不合格人数的频率是( )A、0.125 B、0.45 C、0.425 D、1.254. 若方程x2+3x+c=0有实数根,则c的取值范围是( )A、c≤ B、c≤ C、c≥ D、c≥5. 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( ) A、AC=AB B、∠C= ∠BOD C、∠C=∠B D、∠A=∠B0D6. 如图,甲、乙两同学从 地出发,骑自行车在同一条路上行驶到 地,他们离出发地的距离为 和行驶时间 之间的函数关系的图象如图所示,则下列结论错误的是( )
A、AC=AB B、∠C= ∠BOD C、∠C=∠B D、∠A=∠B0D6. 如图,甲、乙两同学从 地出发,骑自行车在同一条路上行驶到 地,他们离出发地的距离为 和行驶时间 之间的函数关系的图象如图所示,则下列结论错误的是( ) A、 、 两地相距 B、甲在途中停留了0.5小时 C、全程乙比甲少用了1小时 D、乙出发后0.5小时追上甲
A、 、 两地相距 B、甲在途中停留了0.5小时 C、全程乙比甲少用了1小时 D、乙出发后0.5小时追上甲二、填空题。
-
7. 我国倡导的“一带一路”建设将促进我国与世界各国的互利合作,“一带一路”地区覆盖总人口约为4400000000人,将数据4400000000用科学记数法表示为.8. 因式分解: .9. 不等式 的解集是.10. 计算: .11. 一组数据1,2,3,x,5的平均数是3,则该组数据的方差是 .12. “对顶角相等”的逆命题是命题(填真或假)13. 设ΔABC 三边分别为 a、b、c,其中 a,b 满足 +(a-b-4)2 =0,则第三边 c的取值范围为 .14. 如图,平行四边形 中,点E在 上,以 为折痕,把△ 向上翻折,点A正好落在 边的点F处 ,若△ 的周长为6,△ 的周长为20,那么 的长为.
 15. 刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径 .此时圆内接正六边形的周长为 ,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为.(参考数据: )
15. 刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径 .此时圆内接正六边形的周长为 ,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为.(参考数据: )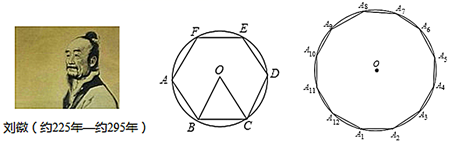 16. 二次函数 ,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为
16. 二次函数 ,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为三、解答题
-
17. 计算:(1)、计算:(2)、化简:18. 根据某网站调查,2019年网民最关注的热点话题分别是:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据绘制的统计图如图:

根据以上信息解答下列问题:
(1)、请补全条形图,并在图中标明相应数据.(2)、若某市中心城区约有90万人口,请你估计该市中心城区最关注教育问题的人数约有多少万人?(3)、据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年关注该问题网民数的年平均增长率约为多少?(已知2017~2019年每年接受调查的网民人数相同, )19. 2019年9月30日,由著名导演李仁港执导的电影《攀登者》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用模球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个不透明的袋子中装有编号1-4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.(1)、请用列表或画树状图的方法表示出随机摸球所有可能的结果;(2)、分别求出小亮和小丽获胜的概率,并判断这种游戏规则对两人公平吗?20. 如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.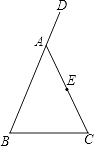 (1)、利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);(2)、试判断AF与BC有怎样的位置关系与数量关系,并说明理由.21. 列分式方程解应用题:
(1)、利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);(2)、试判断AF与BC有怎样的位置关系与数量关系,并说明理由.21. 列分式方程解应用题:“5G改变世界,5G创造未来”.2019年9月,全球首个5G上海虹桥火车站,完成了5G网络深度覆盖,旅客可享受到高速便捷的5G网络服务.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输7千兆数据,5G网络比4G网络快630秒,求5G网络的峰值速率.
22. 疫情突发,危难时刻,从决定建造到交付使用,雷神山、火神山医院仅用时十天,其建造速度之快,充分展现了中国基建的巨大威力!这样的速度和动员能力就是全 国人民的坚定信心和尽快控制疫情的底气!改革开放 年来,中国已经成为领先世界的基 建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点F在线段HG上运动, 垂足为点 的延长线交HG于点 G,经测量 ,
 (1)、求线段 的长度;(结果 精确到 )(2)、连接AF,当线段 时, 求点F和点G之间的距离.(结果精确到0.1m,参考数据: )23. 如图所示,AB是 直径, 弦BC于点F,且交 于点E,且∠AEC=∠ODB.
(1)、求线段 的长度;(结果 精确到 )(2)、连接AF,当线段 时, 求点F和点G之间的距离.(结果精确到0.1m,参考数据: )23. 如图所示,AB是 直径, 弦BC于点F,且交 于点E,且∠AEC=∠ODB.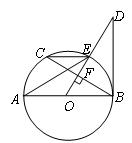 (1)、判断直线 和 的位置关系,并给出证明;(2)、当 , 时,求 的面积.24. 如图,已知二次函数 的图象与坐标轴交于点 和点 .
(1)、判断直线 和 的位置关系,并给出证明;(2)、当 , 时,求 的面积.24. 如图,已知二次函数 的图象与坐标轴交于点 和点 . (1)、求该二次函数的解析式;(2)、已知该函数图象的对称轴上存在一点 ,使得 的周长最小.请求出点 的坐标;(3)、在(2)的条件下,在x轴上找一点M,使得 是等腰三角形,请直接写出所有符合条件的点M的坐标.25. 如图:
(1)、求该二次函数的解析式;(2)、已知该函数图象的对称轴上存在一点 ,使得 的周长最小.请求出点 的坐标;(3)、在(2)的条件下,在x轴上找一点M,使得 是等腰三角形,请直接写出所有符合条件的点M的坐标.25. 如图:
 (1)、如图1,在正方形ABCD中,点E、F分别是BC、CD边上的动点,且 ,求证: .(2)、如图2,在正方形 中,如果点 、 分别是 、 延长线上的动点,且 ,则 、 、 之间数量关系是什么?请写出证明过程.(3)、如图1,若正方形 的边长为6, ,求 的长.26. 如图,点A是坐标原点,点D是反比例函数 图象上一点,点B在x轴上, ,四边形ABCD是平行四边形,BC交反比例函数 图象于点E.
(1)、如图1,在正方形ABCD中,点E、F分别是BC、CD边上的动点,且 ,求证: .(2)、如图2,在正方形 中,如果点 、 分别是 、 延长线上的动点,且 ,则 、 、 之间数量关系是什么?请写出证明过程.(3)、如图1,若正方形 的边长为6, ,求 的长.26. 如图,点A是坐标原点,点D是反比例函数 图象上一点,点B在x轴上, ,四边形ABCD是平行四边形,BC交反比例函数 图象于点E. (1)、平行四边形BCD的面积等于;(2)、设D点横坐标为m,试用m表示点E的坐标;(要有推理和计算过程)(3)、求 的值;(4)、求 的最小值.
(1)、平行四边形BCD的面积等于;(2)、设D点横坐标为m,试用m表示点E的坐标;(要有推理和计算过程)(3)、求 的值;(4)、求 的最小值.