江苏省淮安市淮阴区2020年数学中考二模试卷

试卷更新日期：2020-09-11 类型：中考模拟

进入出卷网下载

一、单选题。

1. 5的相反数是（）

A、 -5 B、5 C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
2. 下面图形分别表示低碳、节水、节能和绿色食品四个标志，其中的轴对称图形是（）

A、 B、 C、 D、

查看试题解析
3. （﹣a²）³=（）

A、a⁵ B、a⁶ C、﹣a⁵ D、﹣a⁶

查看试题解析
4. 如图，若A，B分别是实数a、b在数轴上对应的点，则下列式子的值一定是正数的是（）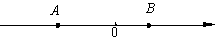

A、b＋a B、b－a C、a^b D、 $\frac{b}{a}$

查看试题解析
5. 已知圆锥的母线长为12，底面圆半径为6，则圆锥的侧面积是（）

A、24π B、36π C、70π D、72π

查看试题解析
6. 某工程队开挖一条480米的隧道，开工后，每天比原计划多挖20米，结果提前4天完成任务，若设原计划每天挖 $x$ 米，那么求 $x$ 时所列方程正确的是（）

A、 $\frac{480}{x - 20} - \frac{480}{x} = 4$ B、 $\frac{480}{x} - \frac{480}{x + 4} = 20$ C、 $\frac{480}{x} - \frac{480}{x + 20} = 4$ D、 $\frac{480}{x - 4} - \frac{480}{x} = 20$

查看试题解析
7. 如图，AB是⊙O的直径，CD是⊙O的弦，连结AC、AD、BD，若∠BAC＝35°，则∠ADC 的度数为

A、35° B、55° C、65° D、70°

查看试题解析

8. 在二次函数

y = - x^{2} + bx + c

中，函数y与自变量x的部分对应值如下表：

x	$- 3$	$- 2$	$- 1$	1	2	3	4	5	6
y	$- 14$	$- 7$	$- 2$	2	m	n	$- 7$	$- 14$	$- 23$

则m、n的大小关系为 $($ $)$

A、

m > n

B、

m < n

C、

m = n

D、无法比较

查看试题解析

二、填空题。

9. 若分式 $\frac{1}{x - 1}$ 有意义，则 $x$ 的取值范围是 .

查看试题解析
10. 据调查，截止2020年2月末，全国4G用户总数达到1230000000户，把1230000000用科学记数法表示为.

查看试题解析
11. “同时抛掷两枚普通的骰子，向上一面的点数之和为13”是（选填“必然事件”，“不可能事件”，或“随机事件”）.

查看试题解析
12. 已知一元二次方程 $x^{2} + x + m = 0$ 的一个根为2，则它的另一个根为.

查看试题解析
13. 一个不透明的布袋里装有8个只有颜色不同的球，其中3个红球，5个白球，从布袋中随机摸出一个球，摸出的球是白球的概率是.

查看试题解析
14. 如图，在△ABC中，AC＝BC，把△ABC沿AC翻折，点B落在点D处，连接BD，若∠CBD＝16°，则∠BAC＝°．

查看试题解析
15. 已知一次函数y＝ $\frac{3}{2}$ x－3的图象与x、y轴分别交于点A、B，与反比例函数y＝ $\frac{k}{x}$ (x＞0)的图象交于点C，且AB＝AC，则k的值为.

查看试题解析
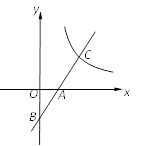16. 如图，在四边形ABCD中，AD∥BC (BC＞AD)，∠D＝90°，∠ABE＝45°，BC＝CD，
若AE＝5，CE=2，则BC的长度为．

查看试题解析

三、解答题

17. 计算：

(1)、解方程： $\frac{2 x}{x - 3} = 1 - \frac{1}{3 - x}$ ；

(2)、计算： $\sqrt[3]{8} + 2 \cos 45^{°} + {(- \frac{1}{2})}^{- 1}$ .

查看试题解析
18. 先化简，再求值：（1﹣ $\frac{1}{a - 1}$ ）÷ $\frac{a^{2} - 4}{a - 1}$ .其中a=﹣3.

查看试题解析
19. $Δ A B C$ 中， $A B = A C$ ， $∠ A = 36 °$ ，AC的垂直平分线交AB于E，D为垂足，连结EC.

(1)、求 $∠ E C D$ 的度数；

(2)、若 $C E = 5$ ，求 $B C$ 长.

查看试题解析
20. 如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．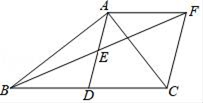

(1)、求证：△AEF≌△DEB；

(2)、若∠BAC＝90°，求证：四边形ADCF是菱形．

查看试题解析
21. 如图，高楼顶部有一信号发射塔（FM），在矩形建筑物ABCD的D、C两点测得该塔顶端F的仰角分别为 $45 ° 、 64.5 °$ ，矩形建筑物高度DC为22米.求该信号发射塔顶端到地面的距离FG.（精确到1m）（参考数据： $sin 64.5 ° \approx 0.90 ， cos 64.5 ° \approx 0.43 ，$ $tan 64.5 ° \approx 2.1$ ）

查看试题解析
22. 为了弘扬中国传统文化，某校对全校学生进行了古诗词知识测试，将测试成绩分为一般、良好、优秀三个等级.从中随机抽取部分学生的测试成绩，绘制成如下两幅统计图，根据图中的信息，解答下列问题：

(1)、本次抽样调查的样本容量是，扇形统计图中阴影部分扇形的圆心角是度；

(2)、将条形统计图补充完整；

(3)、根据本次抽样调查的结果，试估计该校2000名学生中测试成绩为良好和优秀的共有多少人.

查看试题解析
23. 在△ABC中，AB=6，AC=8，D、E分别在AB、AC上，连接DE，设BD=x（0＜x＜6），CE=y（0＜y＜8）．

(1)、当x=2，y=5时，求证：△AED∽△ABC；

(2)、若△ADE和△ABC相似，求y与x的函数表达式．

查看试题解析
24. 如图，△ABC内接于⊙O，且AB为⊙O的直径，OD⊥AB，与AC交于点E，∠D＝2∠A.

(1)、求证：CD是⊙O的切线；

(2)、求证：DE＝DC；

(3)、若OD＝5，CD＝3，求AC的长.

查看试题解析
25. 如图①，点A表示小明家，点B表示学校．小明妈妈骑车带着小明去学校，到达C处时发现数学书没带，于是妈妈立即骑车原路回家拿书后再追赶小明，同时小明步行去学校，到达学校后等待妈妈．假设拿书时间忽略不计，小明和妈妈在整个运动过程中分别保持匀速．妈妈从C处出发x分钟时离C处的距离为y₁米，小明离C处的距离为y₂米，如图②，折线O-D-E-F表示y₁与x的函数图象；折线O-G-F表示y₂与x的函数图象．

(1)、小明的速度为m/min，图②中a的值为．

(2)、设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米．
①写出小明妈妈在骑车由C处返回到A处的过程中，y与x的函数表达式及x的取值范围；
②在图③中画出整个过程中y与x的函数图象．（要求标出关键点的坐标）

查看试题解析
26. 如图，二次函数y＝ax²+bx+4与y轴交于C点，与x轴交于A、B两点，其中A点坐标为(﹣2，0)，B点坐标为(8，0).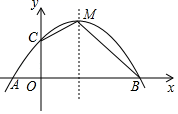

(1)、求经过A，B，C三点的抛物线的解析式；

(2)、如果M为抛物线的顶点，连接CM、BM，求四边形COBM的面积.

查看试题解析
27. 已知，A（0，8），B（4，0），直线y＝﹣x沿x轴作平移运动，平移时交OA于D，交OB于C.

(1)、当直线y＝﹣x从点O出发以1单位长度/s的速度匀速沿x轴正方向平移，平移到达点B时结束运动，过点D作DE⊥y轴交AB于点E，连接CE，设运动时间为t（s）.
①是否存在t值，使得△CDE是以CD为腰的等腰三角形？如果能，请直接写出相应的t值；如果不能，请说明理由.

②将△CDE沿DE翻折后得到△FDE，设△EDF与△ADE重叠部分的面积为y（单位长度的平方）.求y关于t的函数关系式及相应的t的取值范围；

(2)、若点M是AB的中点，将MC绕点M顺时针旋转90°得到MN，连接AN，请直接写出AN+MN的最小值.

查看试题解析