江苏省宿迁市2019-2020学年高二下学期数学期末考试试卷

试卷更新日期：2020-09-11 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {0, 1, 2, 3}$ ， $B = {x | 1 < x < 3}$ ，则 $A \cap B =$ （）

A、 ${1, 2}$ B、 ${0, 1, 2}$ C、 ${2}$ D、 ${2, 3}$

查看试题解析
2. 若复数 $z = \frac{a + i}{1 + i}$ ( $i$ 为虚数单位)为纯虚数，则实数 $a$ 的值为（）

A、1 B、0 C、 $- \frac{1}{2}$ D、-1

查看试题解析
3. 设 $x \in R$ 则“ $x^{2} > 9$ ”是“ $3^{x} > 81$ ”的（）条件

A、充分不必要 B、必要不充分 C、充分必要 D、既不充分也不必要

查看试题解析
4. 函数 $f (x) = \frac{2}{\sqrt{2 - x}} - \log_{2} x$ 的定义域为（）

A、 $(0, 2)$ B、 $(0, 2]$ C、 $(2, + \infty)$ D、 $[2, + \infty)$

查看试题解析
5. 若实数 $m$ ， $n$ 满足 $m > n$ ，则下列选项正确的是（）

A、 $\lg (m - n) > 0$ B、 ${(\frac{1}{2})}^{m} > {(\frac{1}{2})}^{n}$ C、 $m^{3} - n^{3} > 0$ D、 $| m | > | n |$

查看试题解析
6. 夏日炎炎，雪糕成为很多人的解暑甜品，一个盒子里装有10个雪糕，其中草莓味2个，巧克力味3个，芒果味5个，假设三种口味的雪糕外观完全相同，现从中任意取3个，则恰好有一个是芒果味的概率为（）

A、 $\frac{5}{12}$ B、 $\frac{1}{3}$ C、 $\frac{1}{12}$ D、 $\frac{1}{2}$

查看试题解析
7. 某种产品的广告费支出与销售额之间有如下对应数据：

广告费用 $x$ (万元)

0.2

0.4

0.5

0.6

0.8

销售额 $y$ (万元)

3

4

6

5

7

销售额 $y$ (万元)与广告费用 $x$ (万元)之间有线性相关关系，回归方程为 $\hat{y} = 7 x + m$ ( $m$ 为常数)，现在要使销售额达到7.8万元，估计广告费用约为（）万元.

A、0.75 B、0.9 C、1.5 D、2.5

查看试题解析
8. 函数 $f (x) = \frac{\ln (x + 2)}{x - 1}$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、多选题

9. 在100件产品中，有98件合格品，2件不合格品，从这100件产品中任意抽出3件，则下列结论正确的有（）

A、抽出的3件产品中恰好有1件是不合格品的抽法有 $C_{2}^{1} C_{98}^{2}$ 种 B、抽出的3件产品中恰好有1件是不合格品的抽法有 $C_{2}^{1} C_{99}^{2}$ 种 C、抽出的3件中至少有1件是不合格品的抽法有 $C_{2}^{1} C_{98}^{2} + C_{2}^{2} C_{98}^{1}$ 种 D、抽出的3件中至少有1件是不合格品的抽法有 $C_{100}^{3} - C_{98}^{3}$ 种

查看试题解析
10. 已知函数 $y = f (x)$ 的导函数的图象如图所示，下列结论中正确的是（）

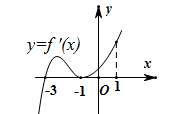A、-1是函数 $f (x)$ 的极小值点 B、-3是函数 $f (x)$ 的极小值点 C、函数 $f (x)$ 在区间 $(- 3 ， 1)$ 上单调递增 D、函数 $f (x)$ 在 $x = 0$ 处切线的斜率小于零

查看试题解析
11. 若函数 $f (x)$ 在定义域 $D$ 内的某个区间 $I$ 上是单调增函数，且 $F (x) = \frac{f (x)}{x}$ 在区间 $I$ 上也是单调增函数，则称 $y = f (x)$ 是 $I$ 上的“一致递增函数”.已知 $f (x) = x + \frac{e^{x}}{x}$ ，若函数 $f (x)$ 是区间 $I$ 上的“一致递增函数”，则区间 $I$ 可能是（）

A、 $(- \infty ， - 2)$ B、 $(- \infty ， 0)$ C、 $(0 ， + \infty)$ D、 $(2 ， + \infty)$

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} - x^{2} - 3 x ， x < 0 \\ f (x - 3) ， x \geq 0 \end{array}$ ，以下结论正确的是（）

A、 $f (x)$ 在区间 $[4 ， 6]$ 上是增函数 B、 $f (- 2) + f (2020) = 4$ C、若函数 $y = f (x) - b$ 在 $(- \infty ， 6)$ 上有6个零点 $x_{i} (i = 1 ， 2 ， 3 ， 4 ， 5 ， 6)$ ，则 $\sum_{i = 1}^{6} x_{i} = 9$ D、若方程 $f (x) = k x + 1$ 恰有3个实根，则 $k \in (- 1 ， - \frac{1}{3}) \cup {1}$

查看试题解析

三、填空题

13. 已知随机变量 $X ~ N (2, σ^{2})$ ， $P (X \leq 6) = 0.9$ ，那么 $P (X \leq - 2)$ 的值为.

查看试题解析
14. 已知 $a = {0.2}^{- 3.2}$ ， $b = \log_{2.2} 0.3$ ， $c = \log_{0.2} 0.3$ ，则 $a, b, c$ 三个数按照从小到大的顺序是.

查看试题解析
15. 现有5位学生站成一排照相，要求 $A$ 和 $B$ 两位学生均在学生 $C$ 的同侧，则不同的排法共有种(用数字作答).

查看试题解析

四、双空题

16. 已知函数 $f (x) = {\begin{array}{l} \frac{1}{3} x^{2} + 2 a x ， x \geq 0 \\ - \frac{1}{3} x^{2} - \frac{2}{3} x ， x < 0 \end{array}$ 的图象关于原点对称，则 $a =$ ；若关于 $x$ 的不等式 $f (b x - 2) > f (1)$ 在区间 $[1 ， 2]$ 上恒成立，则实数 $b$ 的取值范围为.

查看试题解析

五、解答题

17. 已知 ${(2 x + \frac{1}{\sqrt{x}})}^{n}$ 展开式中前三项的二项式系数和为22.

(1)、求 $n$ 的值；

(2)、求展开式中的常数项.

查看试题解析
18. 已知函数 $f (x) = 2 x^{3} - 3 a x^{2} - 2$ ，其中 $a \in R$ .

(1)、求 $a = 1$ ，求 $f (x)$ 在 $[0 ， 2]$ 上的最大值和最小值；

(2)、若 $x = 2$ 是函数 $f (x)$ 的一个极值点，求实数 $a$ 的值.

查看试题解析
19. 某位同学参加3门课程的考试，假设他第一门课程取得优秀的概率为 $\frac{3}{5}$ ，第二､第三门课程取得优秀的概率分别为 $P_{1}, P_{2} (P_{1} > P_{2})$ ，且不同课程是否取得优秀相互独立.记 $ξ$ 为该生取得优秀的课程数，其分布列为

$ξ$

0

1

2

3

$p$

$\frac{6}{125}$

$m$

$n$

$\frac{24}{125}$

(1)、求该同学至少有1门课程取得优秀的概率；

(2)、求 $P_{1}$ ， $P_{2}$ 的值；

(3)、求该同学取得优秀课程数的数学期望 $E (ξ)$ .

查看试题解析
20. 已知函数 $g (x) = \frac{x + b}{a x^{2} + 2}$ ， $x \in (- 1 ， 1)$ ，从下面三个条件中任选一个条件，求出 $a ， b$ 的值，并解答后面的问题.
①已知函数 $f (x) = b + \frac{3}{x - a}$ ，满足 $f (2 - x) + f (x + 2) = 0$ ；

②已知函数 $f (x) = a^{x} + b (a > 0 ， a \neq 1)$ 在 $[1 ， 2]$ 上的值域为 $[2 ， 4]$

③已知函数 $f (x) = x^{2} - a x + 4$ ，若 $f (x + 1)$ 在定义域 $[b - 1 ， b + 1]$ 上为偶函数.

(1)、证明 $g (x)$ 在 $(- 1 ， 1)$ 上的单调性；

(2)、解不等式 $g (t - 1) + g (2 t) < 0$ .

查看试题解析
21. 某医疗机构，为了研究某种病毒在人群中的传播特征，需要检测血液是否为阳性.若现有 $n (n \in N^{*})$ 份血液样本，每份样本被取到的可能性相同，检测方式有以下两种：
方式一：逐份检测，需检测 $n$ 次；

方式二：混合检测，将其中 $k (k \in N^{*} ， k \geq 2)$ 份血液样本分别取样混合在一起检测，若检测结果为阴性，说明这 $k$ 份样本全为阴性，则只需检测1次；若检测结果为阳性，则需要对这 $k$ 份样本逐份检测，因此检测总次数为 $k + 1$ 次，假设每份样本被检测为阳性或阴性是相互独立的，且每份样本为阳性的概率是 $p (0 < p < 1)$ .

(1)、在某地区，通过随机检测发现该地区人群血液为阳性的概率约为0.8%.为了调查某单位该病毒感染情况，随机选取50人进行检测，有两个分组方案：
方案一：将50人分成10组，每组5人；

方案二：将50人分成5组，每组10人.

试分析哪种方案的检测总次数更少？

(取 ${0.992}^{5} = 0.961$ ， ${0.992}^{10} = 0.923$ ， ${0.992}^{11} = 0.915$ )

(2)、现取其中 $k$ 份血液样本，若采用逐份检验方式，需要检测的总次数为 $ξ_{1}$ ；采用混合检测方式，需要检测的总次数为 $ξ_{2}$ .若 $E (ξ_{1}) = E (ξ_{2})$ ，试解决以下问题：
①确定 $p$ 关于 $k$ 的函数关系；

②当 $k$ 为何值时， $p$ 取最大值并求出最大值.

查看试题解析
22. 已知函数 $f (x) = (x - 1) e^{x}$ ， $g (x) = \ln x$ ，其中 $e$ 是自然对数的底数.

(1)、求曲线 $y = f (x)$ 在 $x = 1$ 处的切线方程；

(2)、当 $x \geq 1$ 时，关于 $x$ 不等式 $a g (x) \leq 2 x + 2$ 恒成立，求整数 $a$ 的最大值；

(3)、设函数 $h (x) = b f (x) - g (x)$ ，若函数 $h (x)$ 恰好有2个零点，求实数 $b$ 的取值范围.(取 $\ln 3.5 = 1.25$ ， $\ln 4 = 1.40$ )

查看试题解析

广告费用 $x$ (万元)	0.2	0.4	0.5	0.6	0.8
销售额 $y$ (万元)	3	4	6	5	7

$ξ$	0	1	2	3
$p$	$\frac{6}{125}$	$m$	$n$	$\frac{24}{125}$