广东省佛山市顺德区2019-2020学年七年级上学期数学期中试卷
试卷更新日期:2020-09-10 类型:期中考试
一、单选题
-
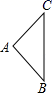
1. ﹣2019的绝对值是( )A、2019 B、﹣2019 C、 D、﹣2. 数32000000用科学记数法表示为( )A、0.32×10 B、3.2×10 C、32×10 D、3.2×103. 三角形ABC绕BC旋转一周得到的几何体为( )
 A、
A、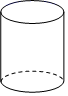 B、
B、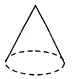 C、
C、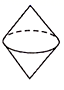 D、
D、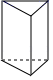 4. 单项式﹣5x2y的次数和系数分别是( )A、3,5 B、3,﹣5 C、2,5 D、2,﹣55. 去括号正确的是( )A、﹣(a﹣1)=a+1 B、﹣(a﹣1)=a﹣1 C、﹣(a﹣1)=﹣a+1 D、﹣(a﹣1)=﹣a﹣16. 下列代数式是同类项的是( )A、 与x2y B、2x2y与3xy2 C、xy与﹣xyz D、x+y与2x+2y7. 对如图所示的几何体认识正确的是( )
4. 单项式﹣5x2y的次数和系数分别是( )A、3,5 B、3,﹣5 C、2,5 D、2,﹣55. 去括号正确的是( )A、﹣(a﹣1)=a+1 B、﹣(a﹣1)=a﹣1 C、﹣(a﹣1)=﹣a+1 D、﹣(a﹣1)=﹣a﹣16. 下列代数式是同类项的是( )A、 与x2y B、2x2y与3xy2 C、xy与﹣xyz D、x+y与2x+2y7. 对如图所示的几何体认识正确的是( ) A、几何体是四棱柱 B、棱柱的侧面是三角形 C、棱柱的底面是四边形 D、棱柱的底面是三角形8. 一个两位数,用x表示十位数字,个位数字比十位数字大3,则这个两位数为( )A、11x+3 B、11x﹣3 C、2x+3 D、2x﹣39. 已知a﹣3b=﹣2,则2a﹣6b+7的值是( )A、11 B、9 C、5 D、310. 下列说法正确的个数是( )
A、几何体是四棱柱 B、棱柱的侧面是三角形 C、棱柱的底面是四边形 D、棱柱的底面是三角形8. 一个两位数,用x表示十位数字,个位数字比十位数字大3,则这个两位数为( )A、11x+3 B、11x﹣3 C、2x+3 D、2x﹣39. 已知a﹣3b=﹣2,则2a﹣6b+7的值是( )A、11 B、9 C、5 D、310. 下列说法正确的个数是( )⑴a的相反数是﹣a;(2)非负数就是正数;(3)正数和负数统称为有理数;(4)|a|=a.
A、3 B、2 C、1 D、0二、填空题
-
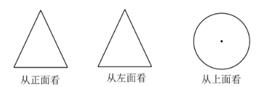
11. ﹣ 的倒数是 .12. 比大小: (填“>”或“<”)13. 如图,是从不同的方向看一个物体得到的平面图形,该物体的形状是。
 14. 计算:(﹣35)+(﹣22)﹣(﹣35)﹣8= .15. 将如图折叠成一个正方体,与“思”字相对的面上的字是 .
14. 计算:(﹣35)+(﹣22)﹣(﹣35)﹣8= .15. 将如图折叠成一个正方体,与“思”字相对的面上的字是 . 16. 已知x、y为有理数,如果规定一种新运算x⊗y=﹣x2+y,则2⊗(﹣3)= .17. 如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推,求出 的值 .
16. 已知x、y为有理数,如果规定一种新运算x⊗y=﹣x2+y,则2⊗(﹣3)= .17. 如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推,求出 的值 .
三、解答题
-
18. 计算题:(﹣2)2×7+(﹣6)÷3﹣|﹣5|19. 化简:(2x2+x)﹣2(3x﹣2x2)20. 某出租车从车站出发在东西方向上营运.若规定向东为正,向西为负,一天的行车情况依先后序记录如下(单位:km):+8,﹣2,﹣4,+4,﹣8,+5,﹣3,﹣6,﹣4,+7.(1)、将最后一名乘客送到目的地,出租车离车站多远?在车站什么方向?(2)、若每千米的营运费为3元,求出司机一天的营运额是多少?21. 已知A=3x2+x﹣2,B=2x2﹣2x﹣1.(1)、化简A+ B;(2)、当x=﹣1时,求A+ B的值.22. 数轴上的点A,B所表示的数如图所示,回答下列问题:
 (1)、求出A,B两点间的距离;(2)、若点A在数轴上移动了m个单位长度到点C,且B,C两点间的距离是3,求m的值.23. 一个正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图.
(1)、求出A,B两点间的距离;(2)、若点A在数轴上移动了m个单位长度到点C,且B,C两点间的距离是3,求m的值.23. 一个正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图. (1)、A对面的字母是 , B对面的字母是;(请直接填写答案)(2)、已知A=x,B=﹣x2+3x,C=﹣3,D=1,E=x2019 , F=6.
(1)、A对面的字母是 , B对面的字母是;(请直接填写答案)(2)、已知A=x,B=﹣x2+3x,C=﹣3,D=1,E=x2019 , F=6.①若字母A表示的数与它对面的字母表示的数互为相反数,求E的值;
②若2A﹣3B+M=0,求出M的表达式.
24. 某综合实践活动园区的门票价为:成人票50元,学生票25元,满40人可以购买团体票,票价打9折(不足40人也可按40人计算),某班在2位老师的带领下到园区参加综合实践活动.(1)、如果学生人数为38人,买门票至少应付多少钱?(2)、如果学生人数为34人,买门票至少应付多少钱?(3)、若设学生人数为x人,你能用含x的代数式表示买门票至少应付多少钱吗?25. 在《丰富的图形世界》一章中,我们认识了三棱柱、四棱柱、五棱柱和六棱柱,这些棱柱是由点、线和面构成.(1)、请使用合适的方式统计上述四种棱柱顶点的个数、棱的条数和面的个数;(2)、若棱柱顶点的个数用V表示、棱的条数用E表示、面的个数用F表示,观察你的统计数据,写出V,E,F三者间的数量关系;(3)、若某几何体满足(2)的数量关系,且有24条棱和10个面,则几何体有多少个顶点?