安徽省合肥市包河区2019-2020学年七年级上学期数学期中试卷

试卷更新日期：2020-09-10 类型：期中考试

进入出卷网下载

一、单选题

1. 在1，-0.1，0，-2这四个数中，最小的数是（）

A、0 B、-0.1 C、-2 D、1

查看试题解析
2. 下列去（添）括号正确的是（）

A、 $x - (y - z) = x - y - z$ B、 $- (x - y + z) = - x - y - z$ C、 $x + 2 y - 2 z = x - 2 (y - z)$ D、 $- a + c + d + b = - (a - b) + (c + d)$

查看试题解析
3. 在 $- (- 2)$ 、 $- | - 2 |$ 、 $- 2^{2}$ 、 ${(- 2)}^{2}$ 中正数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 港珠澳大桥东起香港国际机场附近的香港口岸人工岛，向西横跨伶仃洋海域后连接珠海和澳门人工岛，止于珠海洪湾；桥隧全长55千米，用科学记数法表示这个数为（）

A、55×10⁴m B、5.5×10³ m C、5.5×10⁴m D、0.55×10³m

查看试题解析
5. 已知一个多项式与3x²+9x的和等于5x²+4x﹣1，则这个多项式是（）

A、2x²﹣5x﹣1 B、﹣2x²+5x+1 C、8x²﹣5x+1 D、8x²+13x﹣1

查看试题解析
6. 如图1，将一个边长为a的正方形纸片剪去两个小矩形，得到一个“S”形的图案，如图2所示，则这个“S”形下的图案的周长可表示为（）

A、 $4 a - 8 b$ B、 $8 a - 4 b$ C、 $8 a - 8 b$ D、 $4 a - 10 b$

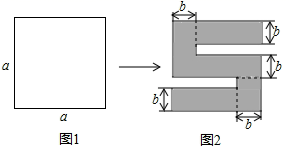查看试题解析
7. 某商店举行促销活动，其促销的方式是“消费超过100元时，所购买的商品按原价打8折后，再减少20元”．若某商品的原价为x元（x＞100），则购买该商品实际付款的金额（单位：元）是（）

A、80%x﹣20 B、80%（x﹣20） C、20%x﹣20 D、20%（x﹣20）

查看试题解析
8. 当 $x = 1$ 时，代数式 $p x^{3} + q x + 1$ 的值为2019，则当 $x = - 1$ 时，代数式 $p x^{3} + q x + 1$ 的值为（）

A、-2017 B、-2019 C、2018 D、2019

查看试题解析
9. 已知a、b为有理数，下列式子：①|ab|＞ab；② $\frac{a}{b} < 0$ ；③ $| \frac{a}{b} | = - \frac{a}{b}$ ；④a³+b³=0，其中一定能够表示a、b异号的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 下面每个表格中的四个数都是按相同规律填写的：
$\begin{matrix} 1 & 4 \\ 2 & 9 \end{matrix}$     $\begin{matrix} 2 & 6 \\ 3 & 20 \end{matrix}$      $\begin{matrix} 3 & 8 \\ 4 & 35 \end{matrix}$      $\begin{matrix} 4 & 10 \\ 5 & 54 \end{matrix}$ …… $\begin{matrix} a & 20 \\ b & x \end{matrix}$ ……

第1个      第2个       第3个      第4个

根据此规律确定x的值为（    ）．

A、135 B、170 C、209 D、252

查看试题解析

二、填空题

11. 将数轴上表示﹣1的点A向右移动5个单位长度，此时点A所对应的数为．

查看试题解析
12. 单项式 $- \frac{a b c}{6}$ 的系数为．

查看试题解析
13. 已知a与b互为相反数，c与d互为倒数，则|a+b|﹣cd＝．

查看试题解析
14. 嘉淇准备完成题目：化简：（4x²﹣6x+7）﹣（4x²﹣口x+2）发现系数“口”印刷不清楚，妈妈告诉她：“我看到该题标准答案的结果是常数”，则题目中“口”应是．

查看试题解析
15. 如果单项式 $- x y^{b + 1}$ 与 $x^{a - 2} y^{3}$ 是同类项，那么 ${(a - b)}^{2019} =$ ．

查看试题解析
16.
如图，数轴上，点A的初始位置表示的数为1，现点A做如下移动：第1次点A向左移动3个单位长度至点A₁ ，第2次从点A₁向右移动6个单位长度至点A₂ ，第3次从点A₂向左移动9个单位长度至点A₃ ， …，按照这种移动方式进行下去，如果点A_n与原点的距离不小于20，那么n的最小值是．

查看试题解析

三、解答题

17. 计算：

(1)、 $- 15 - (- \frac{3}{4}) + 7 - | - 0.75 |$ ；

(2)、 $- (3 a^{2} - 4 a^{2} - 4 a b) + [a^{2} - 2 (2 a^{2} + 2 a b)]$ ；

(3)、 $- 1^{4} + {(- 2)}^{3} \div 4 \times [5 - {(- 3)}^{2}]$ ．

查看试题解析
18. 解方程： $\frac{4 x - 3}{5} - 1 = \frac{2 x - 2}{3}$ ．

查看试题解析
19. 设 $A = a^{2} + 4 a b - 5$ ， $B = a^{2} - 6 a b + 9$ ．

(1)、求 $2 A - B$ 的值．

(2)、若 ${(a - 6)}^{2} + | b + \frac{2}{3} | = 0$ ，求（1）中所求结果的值．

查看试题解析
20. 对于任意有理数a和b ，我们规定： $a * b = a^{2} - 2 a b$ ，如 $3 * 4 = 3^{2} - 2 \times 3 \times 4 = - 15$ ．

(1)、求 $(- 5) * 6$ 的值；

(2)、若 $(- 3) * x = 10$ ，求x的值．

查看试题解析
21. 阅读材料：我们知道，4x﹣2x+x＝（4﹣2+1）x＝3x ，类似地，我们把（a+b）看成一个整体，则4（a+b）﹣2（a+b）+（a+b）＝（4﹣2+1）（a+b）＝3（a+b）．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．

(1)、尝试应用：
把（a﹣b）²看成一个整体，合并3（a﹣b）²﹣6（a﹣b）²+2（a﹣b）²的结果是．

(2)、已知x²﹣2y＝4，求3x²﹣6y﹣21的值；

(3)、拓广探索：
已知a﹣2b＝3，2b﹣c＝﹣5，c﹣d＝10，求（a﹣c）+（2b﹣d）﹣（2b﹣c）的值．

查看试题解析
22. 已知数轴上点A表示的数为6，B是数轴上在左侧的一点，且A，B两点间的距离为10。动点P从点A出发，以每秒6个单位长度的度沿数轴向左匀速运动，设运动时间为t $(t > 0)$ 秒。

(1)、数轴上点B表示的数是；当点P运动到AB的中点时，它所表示的数是。

(2)、动点Q从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，求：
①当点P运动多少秒时，点P追上点Q？

②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？

查看试题解析
23. 取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1，这个结论在数学上还没有得到证明．但举例验证都是正确的，例如；取自然数5．经过下面5步运算可得I，即：如图所示．如果自然数m恰好经过了步运算可得到1，则所有符合条件的m的值有．
$5 \overset{\times 3 + 1}{\to} 16 \overset{+ 2}{\to} 8 \overset{+ 2}{\to} 4 \overset{+ 2}{\to} 2 \overset{+ 2}{\to} 1$

查看试题解析