2020年江苏省中考数学分类汇编专题13 锐角三角函数
试卷更新日期:2020-09-10 类型:二轮复习
一、单选题
-
1. 下列选项错误的是( )A、 B、 C、 D、2. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
 A、 B、 C、 D、3. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A、 B、 C、 D、3. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )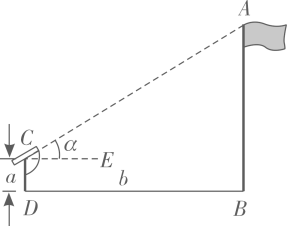 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
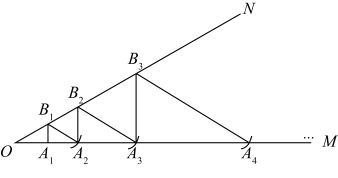
4. 如图, ,在 上截取 .过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;按此规律,所得线段 的长等于.
 5. 如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
5. 如图,测角仪CD竖直放在距建筑物AB底部5m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪的高度是1.5m,则建筑物AB的高度约为m.(结果保留小数点后一位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19) 6. 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 ,则螺帽边长 cm.
6. 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 ,则螺帽边长 cm.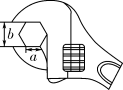 7. 数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形 中, .如图,建立平面直角坐标系 ,使得边 在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是.
7. 数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形 中, .如图,建立平面直角坐标系 ,使得边 在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是.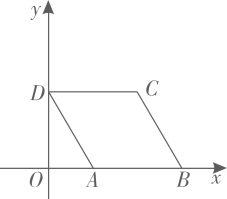 8. 如图,点C在线段 上,且 ,分别以 、 为边在线段 的同侧作正方形 、 ,连接 、 ,则 .
8. 如图,点C在线段 上,且 ,分别以 、 为边在线段 的同侧作正方形 、 ,连接 、 ,则 . 9. 如图,在 中, ,D、E分别是 、 的中点,连接 ,在直线 和直线 上分别取点F、G,连接 、 .若 ,且直线 与直线 互相垂直,则 的长为.
9. 如图,在 中, ,D、E分别是 、 的中点,连接 ,在直线 和直线 上分别取点F、G,连接 、 .若 ,且直线 与直线 互相垂直,则 的长为.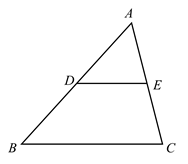
三、解答题
-
10.(1)、计算:4sin60°﹣ +( ﹣1)0;(2)、化简(x+1)÷(1+ ).11. 小红和爸爸绕着小区广场锻炼如图在矩形广场 边 的中点 处有一座雕塑.在某一时刻,小红到达点 处,爸爸到达点 处,此时雕塑在小红的南偏东 方向,爸爸在小红的北偏东 方向,若小红到雕塑的距离 ,求小红与爸爸的距离 .(结果精确到 ,参考数据: , , )
 12. 如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)
12. 如图,点E与树AB的根部点A、建筑物CD的底部点C在一条直线上,AC=10m.小明站在点E处观测树顶B的仰角为30°,他从点E出发沿EC方向前进6m到点G时,观测树顶B的仰角为45°,此时恰好看不到建筑物CD的顶部D(H、B、D三点在一条直线上).已知小明的眼睛离地面1.6m,求建筑物CD的高度(结果精确到0.1m).(参考数据: ≈1.41, ≈1.73.)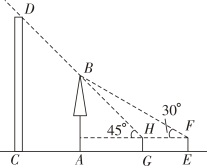 13. 我市在凤城河风景区举办了端午节赛龙舟活动,小亮在河畔的一幢楼上看到一艘龙舟迎面驶来,他在高出水面 的 处测得在 处的龙舟俯角为 ;他登高 到正上方的 处测得驶至 处的龙舟俯角为 ,问两次观测期间龙舟前进了多少?(结果精确到 ,参考数据: , , , )
13. 我市在凤城河风景区举办了端午节赛龙舟活动,小亮在河畔的一幢楼上看到一艘龙舟迎面驶来,他在高出水面 的 处测得在 处的龙舟俯角为 ;他登高 到正上方的 处测得驶至 处的龙舟俯角为 ,问两次观测期间龙舟前进了多少?(结果精确到 ,参考数据: , , , ) 14. 如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从观测站A测得船C在北偏东45°的方向,从观测站B测得船C在北偏西30°的方向.求船C离观测站A的距离.
14. 如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从观测站A测得船C在北偏东45°的方向,从观测站B测得船C在北偏西30°的方向.求船C离观测站A的距离.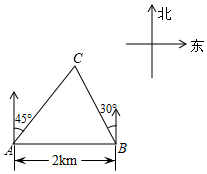 15. 如图,在 中, 的平分线 交 于点 .求 的长?
15. 如图,在 中, 的平分线 交 于点 .求 的长?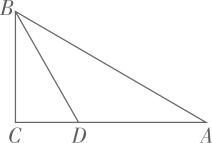 16. 如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据: , , , , , )
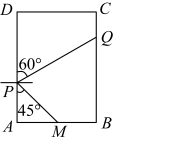
16. 如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据: , , , , , )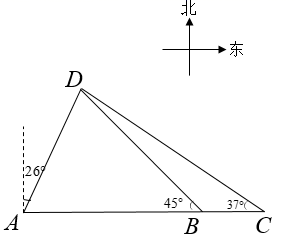 17. 木门常常需要雕刻美丽的图案.(1)、图①为某矩形木门示意图,其中 长为200厘米, 长为100厘米,阴影部分是边长为30厘米的正方形雕刻模具,刻刀的位置在模具的中心点P处,在雕刻时始终保持模具的一边紧贴木门的一边,所刻图案如虚线所示,求图案的周长;
17. 木门常常需要雕刻美丽的图案.(1)、图①为某矩形木门示意图,其中 长为200厘米, 长为100厘米,阴影部分是边长为30厘米的正方形雕刻模具,刻刀的位置在模具的中心点P处,在雕刻时始终保持模具的一边紧贴木门的一边,所刻图案如虚线所示,求图案的周长;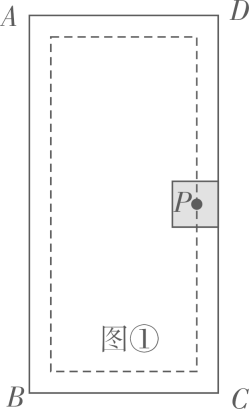 (2)、如图 ,对于(1)中的木门,当模具换成边长为 厘米的等边三角形时,刻刀的位置仍在模具的中心点P处,雕刻时也始终保持模具的一边紧贴本门的一边,使模具进行滑动雕刻.但当模具的一个顶点与木门的一个顶点重合时,需将模具绕着重合点进行旋转雕刻,直到模具的另一边与木门的另一边重合.再滑动模具进行雕刻,如此雕刻一周,请在图 中画出雕刻所得图案的草图,并求其周长.
(2)、如图 ,对于(1)中的木门,当模具换成边长为 厘米的等边三角形时,刻刀的位置仍在模具的中心点P处,雕刻时也始终保持模具的一边紧贴本门的一边,使模具进行滑动雕刻.但当模具的一个顶点与木门的一个顶点重合时,需将模具绕着重合点进行旋转雕刻,直到模具的另一边与木门的另一边重合.再滑动模具进行雕刻,如此雕刻一周,请在图 中画出雕刻所得图案的草图,并求其周长.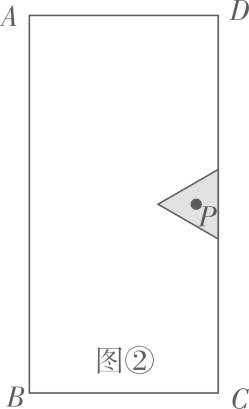 18. 问题1:如图①,在四边形 中, , 是 上一点, , .
18. 问题1:如图①,在四边形 中, , 是 上一点, , .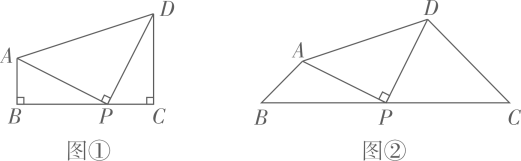 (1)、求证: .(2)、如图②,在四边形 中, , 是 上一点, , .求 的值.19. 如图,正方形 的边长为6, 为 的中点, 为等边三角形,过点 作 的垂线分别与边 、 相交于点 、 ,点 、 分别在线段 、 上运动,且满足 ,连接 .
(1)、求证: .(2)、如图②,在四边形 中, , 是 上一点, , .求 的值.19. 如图,正方形 的边长为6, 为 的中点, 为等边三角形,过点 作 的垂线分别与边 、 相交于点 、 ,点 、 分别在线段 、 上运动,且满足 ,连接 .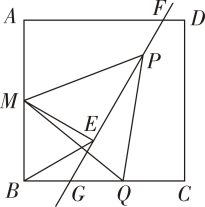 (1)、求证: .(2)、当点 在线段 上时,试判断 的值是否变化?如果不变,求出这个值,如果变化,请说明理由.(3)、设 ,点 关于 的对称点为 ,若点 落在 的内部,试写出 的范围,并说明理由.20. 以下虚线框中为一个合作学习小组在一次数学实验中的过程记录,请阅读后完成虚线框下方的问题 .
(1)、求证: .(2)、当点 在线段 上时,试判断 的值是否变化?如果不变,求出这个值,如果变化,请说明理由.(3)、设 ,点 关于 的对称点为 ,若点 落在 的内部,试写出 的范围,并说明理由.20. 以下虚线框中为一个合作学习小组在一次数学实验中的过程记录,请阅读后完成虚线框下方的问题 .Ⅰ.在 中, ,在探究三边关系时,通过画图,度量和计算,收集到,组数据如下表:(单位:厘米)
2.8
2.7
2.6
2.3
2
1.5
0.4
0.4
0.8
1.2
1.6
2
2.4
2.8
3.2
3.5
3.8
3.9
4
3.9
3.2
Ⅱ.根据学习函数的经验,选取上表中 和 的数据进行分析;
设 ,以 为坐标,在图 所示的坐标系中描出对应的点;
连线;
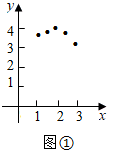
Ⅲ.观察思考
结合表中的数据以及所面的图像,猜想.当 ▲ 时,y最大;
Ⅳ.进一步C猜想:若 中, ,斜边 为常数, ),则 ▲ 时, 最大.
推理证明
Ⅴ.对(4)中的猜想进行证明.
(1)、问题1.在图 中完善(1)的描点过程,并依次连线;(2)、问题2.补全观察思考中的两个猜想:Ⅲ;Ⅳ。(3)、问题3.证明上述Ⅴ中的猜想:(4)、问题4.图 中折线 是一个感光元件的截面设计草图,其中点 间的距离是4厘米, 厘米, 平行光线从 区域射入, 线段 为感光区城,当 的长度为多少时,感光区域长度之和最大,并求出最大值. 21. 如图1,已知点O在四边形ABCD的边AB上,且 ,OC平分 ,与BD交于点G,AC分别与BD、OD交于点E、F.
21. 如图1,已知点O在四边形ABCD的边AB上,且 ,OC平分 ,与BD交于点G,AC分别与BD、OD交于点E、F.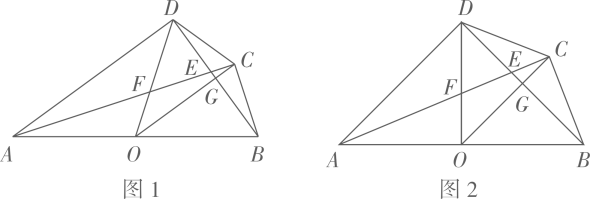 (1)、求证: ;(2)、如图2,若 ,求 的值;(3)、当四边形ABCD的周长取最大值时,求 的值.22. 筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为 的筒车 按逆时针方向每分钟转 圈,筒车与水面分别交于点A、B,筒车的轴心 距离水面的高度 长为 ,简车上均匀分布着若干个盛水筒.若以某个盛水筒 刚浮出水面时开始计算时间.
(1)、求证: ;(2)、如图2,若 ,求 的值;(3)、当四边形ABCD的周长取最大值时,求 的值.22. 筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为 的筒车 按逆时针方向每分钟转 圈,筒车与水面分别交于点A、B,筒车的轴心 距离水面的高度 长为 ,简车上均匀分布着若干个盛水筒.若以某个盛水筒 刚浮出水面时开始计算时间.
 (1)、经过多长时间,盛水筒 首次到达最高点?(2)、浮出水面3.4秒后,盛水筒P距离水面多高?(3)、若接水槽 所在直线是 的切线,且与直线 交于点M, .求盛水筒P从最高点开始,至少经过多长时间恰好在直线 上.(参考数据: , , )
(1)、经过多长时间,盛水筒 首次到达最高点?(2)、浮出水面3.4秒后,盛水筒P距离水面多高?(3)、若接水槽 所在直线是 的切线,且与直线 交于点M, .求盛水筒P从最高点开始,至少经过多长时间恰好在直线 上.(参考数据: , , )