初中数学北师大版八年级上学期 第三章 3.3 轴对称与坐标变化

试卷更新日期：2020-09-10 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 在平面直角坐标系中，点 (2 ， −1) 关于x轴对称的点是（    ）
    A、(2 ， 1) B、(1，−2) C、(−1 ， 2) D、(−2 ， −1)

    查看试题解析

  • 2. 已知点M （3，﹣2），N（﹣3，﹣2），则直线MN与x轴、y轴的位置关系分别为（  ）
    A、平行，垂直 B、平行，平行 C、垂直，平行 D、相交，相交

    查看试题解析

  • 3. 如图，在平面直角坐标系中，点 A(3 ， m) 在第一象限，若点A关于x轴的对称点B在直线 y=−x+1 上，则m的值为（    ）

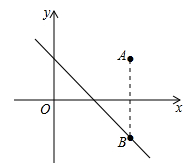    A、-1 B、1 C、2 D、3

    查看试题解析

  • 4. 平面直角坐标中，已知点P（a ， 3）在第二象限，则点P关于直线m（直线m上各点的横坐标都是2）对称的点的坐标是（    ）
    A、（﹣a ， 3） B、（a ， ﹣3） C、（﹣a+2，3） D、（﹣a+4，3）

    查看试题解析

二、填空题

  • 5. 如图，点 P(−2 ， 1) 与点 Q(a ， b) 关于直线 l(y=−1) 对称，则 a+b= ．

    查看试题解析

  • 6. 点A（－2，1）关于x轴对称的点的坐标是 ．

    查看试题解析

三、作图题

  • 7. 如图，在由长度为1个单位长度的小正方形组成的网格中， △ABC 的三个顶点A，B，C都在格点上，分别按下列要求在网格中作图：

    （ 1 ）画出与 △ABC 关于直线l成轴对称的 △A1B1C1 ；

    （ 2 ）在直线l上找出一点P，使得 |PA−PC| 的值最大；（保留作图痕迹，并标上字母P）

    （ 3 ）在直线l上找出一点Q，使得 QA+QC1 的值最小.（保留作图痕迹，并标上字母Q）

    查看试题解析

  • 8. 如图，网格中的 ΔABC 与 ΔDEF 为轴对称图形，且顶点都在格点上.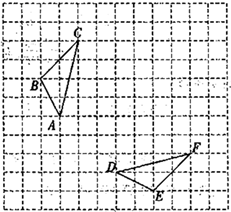

    (1)、利用网格，作出 ΔABC 与 ΔDEF 的对称轴l；
    (2)、结合图形，在对称轴l上画出一点 P ，使得 PA+PC 最小；
    (3)、如果每个小正方形的边长为1，请直接写出 ΔABC 的面积.

    查看试题解析

  • 9. 如图，在平面直角坐标系 xoy 中，A（-1，5），B（-1，0），C（-4，3）

    (1)、在图中作出 △ABC 关于 y 轴的对称图形 △A1B1C1 .
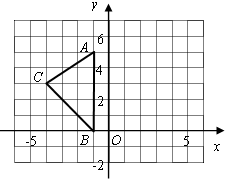    (2)、写出点 A1 ， B1 ， C1 的坐标.
    (3)、求出 △ABC 的面积.

    查看试题解析

  • 10. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）.

    ①在如图所示的网格平面内作出平面直角坐标系；

    ②作出△ABC关于y轴对称的△A′B′C′，并写出点B′的坐标；

    ③P是x轴上的动点，在图中找出使△A′BP周长最短时的点P，直接写出点P的坐标.

    查看试题解析

四、综合题

  • 11. 在平面直角坐标系xOy中， A、B两点分别在x轴、y轴的正半轴上，且OB =OA=3．
    (1)、求点A、B的坐标；
    (2)、已知点C（－2，2），求△ BOC 的面积；
    (3)、点P是第一、三象限角平分线上一点，若 SΔABP=332 ，求点P的坐标．

     

    查看试题解析

  • 12. 在平面直角坐标系中，有点A（a﹣1，3），B（a+2，2a﹣1）
    (1)、若线段AB∥x轴，求点A、B的坐标；
    (2)、当点B到y轴的距离与点A到x轴的距离相等时，求点B所在的象限．

    查看试题解析