2020年江苏省中考数学分类汇编专题12 圆
试卷更新日期:2020-09-10 类型:二轮复习
一、单选题
-
1. 如图是一个几体何的三视图(图中尺寸单位:cm),则这个几何体的侧面积为( )
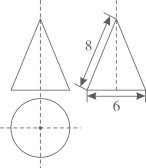 A、48πcm2 B、24πcm2 C、12πcm2 D、9πcm22. 如图,点A,B,C在圆O上, ,则 的度数是( )
A、48πcm2 B、24πcm2 C、12πcm2 D、9πcm22. 如图,点A,B,C在圆O上, ,则 的度数是( ) A、 B、 C、 D、3. 如图, 是 的弦,点C是优弧 上的动点(C不与A、B重合), ,垂足为H,点M是 的中点.若 的半径是3,则 长的最大值是( )
A、 B、 C、 D、3. 如图, 是 的弦,点C是优弧 上的动点(C不与A、B重合), ,垂足为H,点M是 的中点.若 的半径是3,则 长的最大值是( )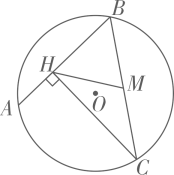 A、3 B、4 C、5 D、64. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )
A、3 B、4 C、5 D、64. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )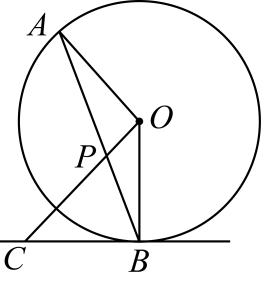 A、 B、 C、 D、5. 如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
A、 B、 C、 D、5. 如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )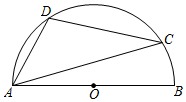 A、10° B、14° C、16° D、26°6. 如图,半径为10的扇形 中, , 为 上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( )
A、10° B、14° C、16° D、26°6. 如图,半径为10的扇形 中, , 为 上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( ) A、 B、 C、 D、7. 如图,在扇形 中,已知 , ,过 的中点C作 , ,垂足分别为D、E,则图中阴影部分的面积为( )
A、 B、 C、 D、7. 如图,在扇形 中,已知 , ,过 的中点C作 , ,垂足分别为D、E,则图中阴影部分的面积为( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 在第一象限,⊙P与x轴、y轴都相切,且经过矩形 的顶点C,与BC相交于点D,若⊙P的半径为5,点 的坐标是 ,则点D的坐标是( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 在第一象限,⊙P与x轴、y轴都相切,且经过矩形 的顶点C,与BC相交于点D,若⊙P的半径为5,点 的坐标是 ,则点D的坐标是( )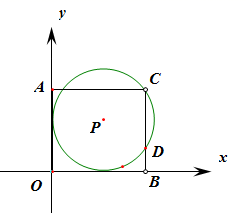 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为cm.10. 如图,已知 是 的直径, 是 的切线,连接 交 于点D,连接 .若 ,则 的度数是 .
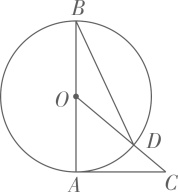 11. 如图,在 中, , , .若以 所在直线为轴,把 旋转一周,得到一个圆锥,则这个圆锥的侧面积等于.
11. 如图,在 中, , , .若以 所在直线为轴,把 旋转一周,得到一个圆锥,则这个圆锥的侧面积等于.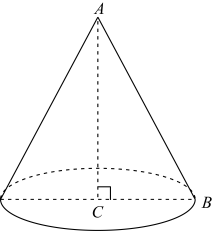 12. 如图, 、 、 、 为一个正多边形的顶点, 为正多边形的中心,若 ,则这个正多边形的边数为.
12. 如图, 、 、 、 为一个正多边形的顶点, 为正多边形的中心,若 ,则这个正多边形的边数为.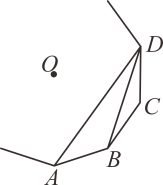 13. 圆锥底面圆半径为5,母线长为6,则圆锥侧面积等于.14. 如图所示的网格由边长为 个单位长度的小正方形组成,点 、 、 、在直角坐标系中的坐标分别为 , , ,则 内心的坐标为.
13. 圆锥底面圆半径为5,母线长为6,则圆锥侧面积等于.14. 如图所示的网格由边长为 个单位长度的小正方形组成,点 、 、 、在直角坐标系中的坐标分别为 , , ,则 内心的坐标为. 15. 如图,直线a⊥b,垂足为 ,点 在直线 上, , 为直线 上一动点,若以 为半径的 与直线 相切,则 的长为.
15. 如图,直线a⊥b,垂足为 ,点 在直线 上, , 为直线 上一动点,若以 为半径的 与直线 相切,则 的长为.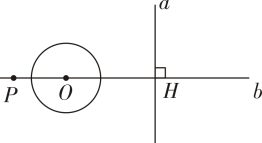 16. 用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为.17. 如图,在 中,点 在 上, 则 。
16. 用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为.17. 如图,在 中,点 在 上, 则 。 18. 圆锥的底面半径为3,侧面积为 ,则这个圆锥的母线长为.19. 已知圆锥的底面半径为 ,高为 ,则它的侧面展开图的面积为=.20. 如图,在边长为 的正六边形 中,点P在BC上,则 的面积为.
18. 圆锥的底面半径为3,侧面积为 ,则这个圆锥的母线长为.19. 已知圆锥的底面半径为 ,高为 ,则它的侧面展开图的面积为=.20. 如图,在边长为 的正六边形 中,点P在BC上,则 的面积为.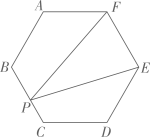 21. 用一个圆心角为 ,半径为 的扇形纸片围成一个圆锥的侧面,这个圆锥的底面圆半径为 .22. 如图,在矩形ABCD中,AB=1,AD= ,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为.
21. 用一个圆心角为 ,半径为 的扇形纸片围成一个圆锥的侧面,这个圆锥的底面圆半径为 .22. 如图,在矩形ABCD中,AB=1,AD= ,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为. 23. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .
23. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .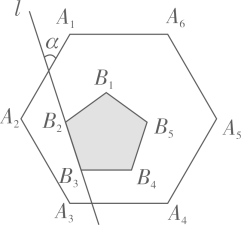
三、解答题
-
24. 如图,▱ABCD中,∠ABC的平分线BO交边AD于点O,OD=4,以点O为圆心,OD长为半径作⊙O,分别交边DA、DC于点M、N.点E在边BC上,OE交⊙O于点G,G为 的中点.
 (1)、求证:四边形ABEO为菱形;(2)、已知cos∠ABC= ,连接AE,当AE与⊙O相切时,求AB的长.25. 如图,在 中,点 为 的中点,弦 、 互相垂直,垂足为 , 分别与 、 相交于点 、 ,连接 、 .
(1)、求证:四边形ABEO为菱形;(2)、已知cos∠ABC= ,连接AE,当AE与⊙O相切时,求AB的长.25. 如图,在 中,点 为 的中点,弦 、 互相垂直,垂足为 , 分别与 、 相交于点 、 ,连接 、 . (1)、求证: 为 的中点.(2)、若 的半径为8, 的度数为 ,求线段 的长.26. 如图,在△ABC中,D是边BC上一点,以BD为直径的⊙O经过点A,且∠CAD=∠ABC.
(1)、求证: 为 的中点.(2)、若 的半径为8, 的度数为 ,求线段 的长.26. 如图,在△ABC中,D是边BC上一点,以BD为直径的⊙O经过点A,且∠CAD=∠ABC.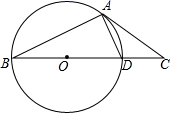 (1)、请判断直线AC是否是⊙O的切线,并说明理由;(2)、若CD=2,CA=4,求弦AB的长.27. 如图, 是 的外接圆, 是 的直径, .
(1)、请判断直线AC是否是⊙O的切线,并说明理由;(2)、若CD=2,CA=4,求弦AB的长.27. 如图, 是 的外接圆, 是 的直径, .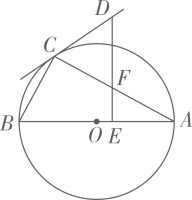 (1)、求证: 是 的切线;(2)、若 ,垂足为 交 与点;求证: 是等腰三角形.28. 如图, 内接于 , ,点E在直径CD的延长线上,且 .
(1)、求证: 是 的切线;(2)、若 ,垂足为 交 与点;求证: 是等腰三角形.28. 如图, 内接于 , ,点E在直径CD的延长线上,且 .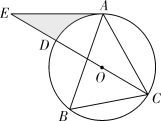 (1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.29. 如图, 过 的圆心,交 于点A、B, 是 的切线,点C是切点,已知 , .
(1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.29. 如图, 过 的圆心,交 于点A、B, 是 的切线,点C是切点,已知 , .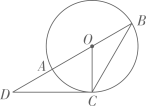 (1)、求证: ;(2)、求 的周长.30. 如图,已知 是锐角三角形 .
(1)、求证: ;(2)、求 的周长.30. 如图,已知 是锐角三角形 .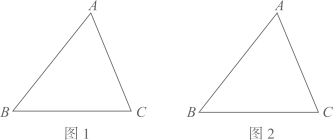 (1)、请在图1中用无刻度的直尺和圆规作图;作直线l,使l上的各点到B、C两点的距离相等;设直线 与 、 分别交于点M、N,作一个圆,使得圆心O在线段 上,且与边 、 相切;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , ,则 的半径为.31. 如图, 是圆O的弦, 是圆 外一点, , 交 于点P,交圆O于点D,且 .
(1)、请在图1中用无刻度的直尺和圆规作图;作直线l,使l上的各点到B、C两点的距离相等;设直线 与 、 分别交于点M、N,作一个圆,使得圆心O在线段 上,且与边 、 相切;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , ,则 的半径为.31. 如图, 是圆O的弦, 是圆 外一点, , 交 于点P,交圆O于点D,且 .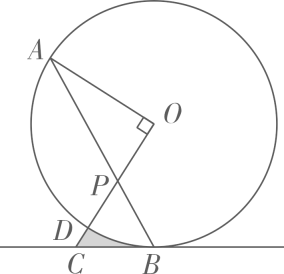 (1)、判断直线 与圆O的位置关系,并说明理由;(2)、若 , ,求图中阴影部分的面积.32. 如图1,点B在线段 上,Rt△ ≌Rt△ , , , .
(1)、判断直线 与圆O的位置关系,并说明理由;(2)、若 , ,求图中阴影部分的面积.32. 如图1,点B在线段 上,Rt△ ≌Rt△ , , , .
 (1)、点F到直线 的距离是;(2)、固定△ ,将△ 绕点C按顺时针方向旋转30°,使得 与 重合,并停止旋转.
(1)、点F到直线 的距离是;(2)、固定△ ,将△ 绕点C按顺时针方向旋转30°,使得 与 重合,并停止旋转.①请你在图1中用直尺和圆规画出线段 经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法)该图形的面积为;
②如图2,在旋转过程中,线段 与 交于点O,当 时,求 的长.
33. 如图,已知 , 是 的平分线,A是射线 上一点, .动点P从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点Q从点O出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点B.经过O、P、Q三点作圆,交 于点C,连接 、 .设运动时间为 ,其中 .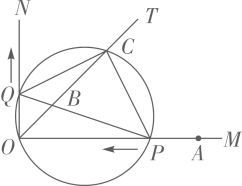 (1)、求 的值;(2)、是否存在实数t,使得线段 的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、求四边形 的面积.34. 如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把 的值称为⊙I关于直线a的“特征数”.
(1)、求 的值;(2)、是否存在实数t,使得线段 的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、求四边形 的面积.34. 如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把 的值称为⊙I关于直线a的“特征数”.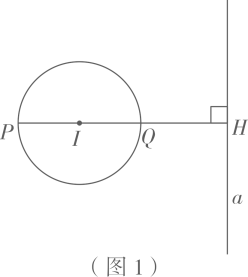
 (1)、如图2,在平面直角坐标系 中,点E的坐标为 ,半径为1的⊙O与两坐标轴交于点A、B、C、D.
(1)、如图2,在平面直角坐标系 中,点E的坐标为 ,半径为1的⊙O与两坐标轴交于点A、B、C、D.①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点_▲__(填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为_▲__;
②若直线n的函数表达式为 ,求 关于直线n的“特征数”;
(2)、在平面直角坐标系 中,直线l经过点 ,点F是坐标平面内一点,以F为圆心, 为半径作⊙F.若⊙F与直线l相离,点 是⊙F关于直线l的“远点”,且⊙F关于直线l的“特征数”是 ,求直线l的函数表达式.