2020年江苏省中考数学分类汇编专题10 四边形
试卷更新日期:2020-09-10 类型:二轮复习
一、单选题
-
1. 正十边形的每一个外角的度数为( )A、 B、 C、 D、2. 下列条件中,能判定▱ABCD是菱形的是( )A、AC=BD B、AB⊥BC C、AD=BD D、AC⊥BD3. 如图,小明从点A出发沿直线前进10米到达点B,向左转 后又沿直线前进10米到达点C,再向左转 后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
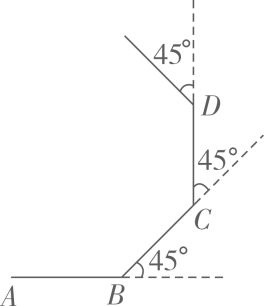 A、100米 B、80米 C、60米 D、40米4. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( )
A、100米 B、80米 C、60米 D、40米4. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( ) A、 B、 C、3 D、55. 如图,将矩形纸片 沿 折叠,使点A落在对角线 上的 处.若 ,则 等于( ).
A、 B、 C、3 D、55. 如图,将矩形纸片 沿 折叠,使点A落在对角线 上的 处.若 ,则 等于( ).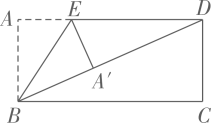 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
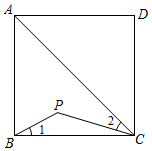
6. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
 7. 如图,在菱形 中, ,点E在 上,若 ,则 .
7. 如图,在菱形 中, ,点E在 上,若 ,则 .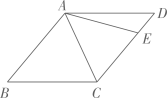 8. 如图,已知 是一个锐角,以点O为圆心,任意长为半径画弧,分别交 、 于点A、B,再分别以点A、B为圆心,大于 长为半径画弧,两弧交于点C,画射线 .过点 作 ,交射线 于点D,过点D作 ,交 于点E.设 , ,则 .
8. 如图,已知 是一个锐角,以点O为圆心,任意长为半径画弧,分别交 、 于点A、B,再分别以点A、B为圆心,大于 长为半径画弧,两弧交于点C,画射线 .过点 作 ,交射线 于点D,过点D作 ,交 于点E.设 , ,则 . 9. 如图,在 中, , , ,点E为边AB上的一个动点,连接ED并延长至点F,使得 ,以EC、EF为邻边构造 ,连接EG,则EG的最小值为.
9. 如图,在 中, , , ,点E为边AB上的一个动点,连接ED并延长至点F,使得 ,以EC、EF为邻边构造 ,连接EG,则EG的最小值为.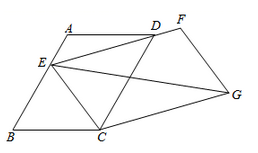
三、解答题
-
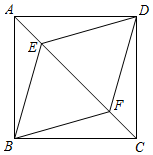
10. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.
 11. 如图, 的对角线AC,BD相交于点O,过点O作 ,分别交AB,DC于点E、F,连接AF、CE.
11. 如图, 的对角线AC,BD相交于点O,过点O作 ,分别交AB,DC于点E、F,连接AF、CE. (1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.12. 如图,在四边形 中, ,对角线 的垂直平分线与边 、 分别相交于M、N.
(1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.12. 如图,在四边形 中, ,对角线 的垂直平分线与边 、 分别相交于M、N.
 (1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的周长.13. 如图,在平行四边形 中,点E、F分别在 、 上, 与 相交于点O,且 .
(1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的周长.13. 如图,在平行四边形 中,点E、F分别在 、 上, 与 相交于点O,且 . (1)、求证: ≌ ;(2)、连接 、 ,则四边形 (填“是”或“不是”)平行四边形.14. 如图,在 中, ,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作 ,交⊙O于点F,求证:
(1)、求证: ≌ ;(2)、连接 、 ,则四边形 (填“是”或“不是”)平行四边形.14. 如图,在 中, ,D是AB上一点,⊙O经过点A、C、D,交BC于点E,过点D作 ,交⊙O于点F,求证: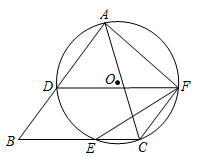 (1)、四边形DBCF是平行四边形(2)、15.(1)、如图1,点P为矩形 对角线 上一点,过点P作 ,分别交 、 于点E、F.若 , , 的面积为 , 的面积为 ,则 ;
(1)、四边形DBCF是平行四边形(2)、15.(1)、如图1,点P为矩形 对角线 上一点,过点P作 ,分别交 、 于点E、F.若 , , 的面积为 , 的面积为 ,则 ;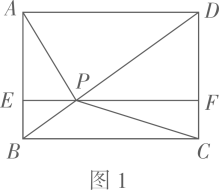 (2)、如图2,点 为 内一点(点 不在 上),点 、 、 、 分别为各边的中点.设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);
(2)、如图2,点 为 内一点(点 不在 上),点 、 、 、 分别为各边的中点.设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);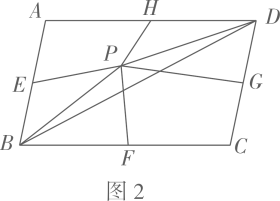 (3)、如图3,点 为 内一点(点 不在 上)过点 作 , ,与各边分别相交于点 、 、 、 .设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);
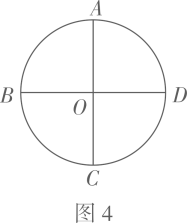
(3)、如图3,点 为 内一点(点 不在 上)过点 作 , ,与各边分别相交于点 、 、 、 .设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);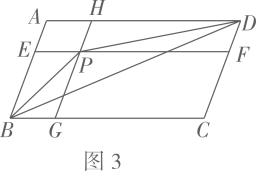 (4)、如图4,点 、 、 、 把 四等分.请你在圆内选一点 (点 不在 、 上),设 、 、 围成的封闭图形的面积为 , 、 、 围成的封闭图形的面积为 , 的面积为 , 的面积为 .根据你选的点 的位置,直接写出一个含有 、 、 、 的等式(写出一种情况即可).
(4)、如图4,点 、 、 、 把 四等分.请你在圆内选一点 (点 不在 、 上),设 、 、 围成的封闭图形的面积为 , 、 、 围成的封闭图形的面积为 , 的面积为 , 的面积为 .根据你选的点 的位置,直接写出一个含有 、 、 、 的等式(写出一种情况即可).