2020年江苏省中考数学分类汇编专题09 平面几何基础与三角形
试卷更新日期:2020-09-10 类型:二轮复习
一、单选题
-
1. 把如图所示的纸片沿着虚线折叠,可以得到的几何体是( )
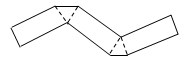 A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥2. 如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数为( )
A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥2. 如图,直线a,b被直线c所截,a∥b,∠1=50°,则∠2的度数为( )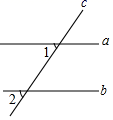 A、40° B、50° C、130° D、150°3. 如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A、40° B、50° C、130° D、150°3. 如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( ) A、36° B、34° C、32° D、30°4. 如图,直线a、b被直线c所截, , ,则 的度数是( )
A、36° B、34° C、32° D、30°4. 如图,直线a、b被直线c所截, , ,则 的度数是( ) A、30° B、40° C、50° D、60°5. 在△ABC中,AB=1,BC= ,下列选项中,可以作为AC长度的是( )A、2 B、4 C、5 D、66. 如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A、30° B、40° C、50° D、60°5. 在△ABC中,AB=1,BC= ,下列选项中,可以作为AC长度的是( )A、2 B、4 C、5 D、66. 如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )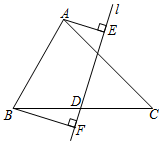 A、 B、2 C、2 D、37. 如图,在四边形 中 , , , ,把 沿着 翻折得到 ,若 ,则线段 的长度为( )
A、 B、2 C、2 D、37. 如图,在四边形 中 , , , ,把 沿着 翻折得到 ,若 ,则线段 的长度为( )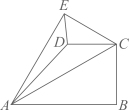 A、 B、 C、 D、8. 如图,在平面直角坐标系中,Q是直线y=﹣ x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点 ,连接 ,则 的最小值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,Q是直线y=﹣ x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点 ,连接 ,则 的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
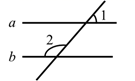
9. 如图,直线 被直线c所截, .那么 .
 10. 如图,在 中, 的垂直平分线分别交 、 于点E、F.若 是等边三角形,则 °.
10. 如图,在 中, 的垂直平分线分别交 、 于点E、F.若 是等边三角形,则 °. 11. 如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 =.
11. 如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 =.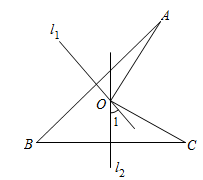 12. 在 中,若 , ,则 的面积的最大值为.13. 如图,在 中, , 、 、 分别为 、 、 的中点,若 ,则 .
12. 在 中,若 , ,则 的面积的最大值为.13. 如图,在 中, , 、 、 分别为 、 、 的中点,若 ,则 .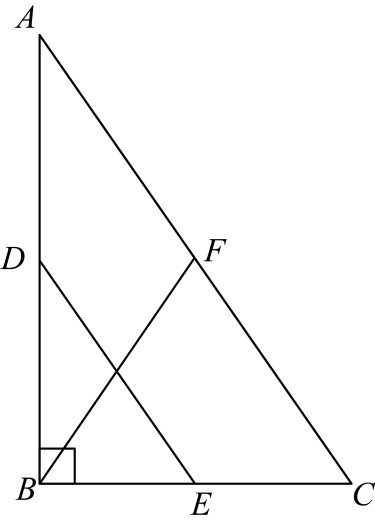 14. 如图,将分别含有 、 角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为 ,则图中角 的度数为.
14. 如图,将分别含有 、 角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为 ,则图中角 的度数为. 15. 如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为.
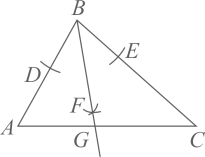
15. 如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为. 16. 如图,在 中,按以下步骤作图:
16. 如图,在 中,按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交AB、BC于点D、E.
②分别以点D、E为圆心,大于 的同样长为半径作弧,两弧交于点F.
③作射线BF交AC于点G.
如果 , , 的面积为18,则 的面积为.
 17. 《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面尺高.
17. 《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面尺高.
三、综合题
-
18. 已知:如图,点A、B、C、D在一条直线上, .
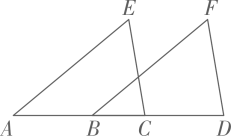 (1)、求证: ;(2)、若 ,求 的度数.19. 如图,已知 , , .
(1)、求证: ;(2)、若 ,求 的度数.19. 如图,已知 , , .

求证:
(1)、 ;(2)、 .20. 如图,点O是正方形, 的中心.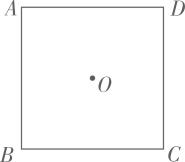 (1)、用直尺和圆规在正方形内部作一点E(异于点O),使得 (保留作图痕迹,不写作法)(2)、连接 求证: .21. 如图, , , . , 与 交于点 .
(1)、用直尺和圆规在正方形内部作一点E(异于点O),使得 (保留作图痕迹,不写作法)(2)、连接 求证: .21. 如图, , , . , 与 交于点 .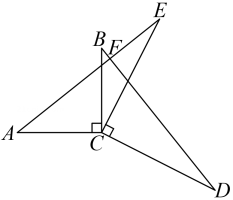 (1)、求证: ;(2)、求 的度数.22. 如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)、求证: ;(2)、求 的度数.22. 如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF. (1)、求证:∠D=∠2;(2)、若EF∥AC,∠D=78°,求∠BAC的度数.23. 如图,已知线段 ,点 在平面直角坐标系 内,
(1)、求证:∠D=∠2;(2)、若EF∥AC,∠D=78°,求∠BAC的度数.23. 如图,已知线段 ,点 在平面直角坐标系 内,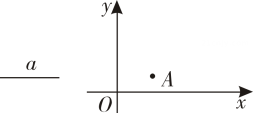 (1)、用直尺和圆规在第一象限内作出点 ,使点 到两坐标轴的距离相等,且与点 的距离等于 .(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 点的坐标为 ,求 点的坐标.24. 如图,在矩形 中, , ,点E为边 上的一点(与C、D不重合)四边形 关于直线 的对称图形为四边形 ,延长 交 与点P,记四边形 的面积为S.
(1)、用直尺和圆规在第一象限内作出点 ,使点 到两坐标轴的距离相等,且与点 的距离等于 .(保留作图痕迹,不写作法)(2)、在(1)的条件下,若 , 点的坐标为 ,求 点的坐标.24. 如图,在矩形 中, , ,点E为边 上的一点(与C、D不重合)四边形 关于直线 的对称图形为四边形 ,延长 交 与点P,记四边形 的面积为S.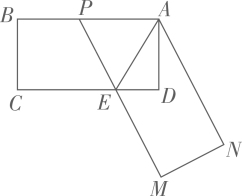 (1)、若 ,求S的值;(2)、设 ,求S关于x的函数表达式.25. 如图
(1)、若 ,求S的值;(2)、设 ,求S关于x的函数表达式.25. 如图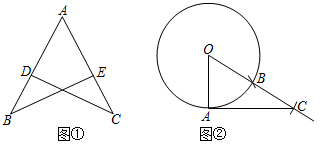 (1)、如图①,点D在AB上,点E在AC上,AD=AE,∠B=∠C.求证:AB=AC.(2)、如图②,A为⊙O上一点,按以下步骤作图:
(1)、如图①,点D在AB上,点E在AC上,AD=AE,∠B=∠C.求证:AB=AC.(2)、如图②,A为⊙O上一点,按以下步骤作图:①连接OA;
②以点A为圆心,AO长为半径作弧,交⊙O于点B;
③在射线OB上截取BC=OA;
④连接AC.
若AC=3,求⊙O的半径.
26. 我们知道:如图①,点 把线段 分成两部分,如果 .那么称点 为线段 的黄金分割点.它们的比值为 . (1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.
(1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.