2020年江苏省中考数学分类汇编专题08 二次函数
试卷更新日期:2020-09-10 类型:二轮复习
一、单选题
-
1. 将二次函数y=(x﹣1)2+2的图象向上平移3个单位长度,得到的拋物线相应的函数表达式为( )A、y=(x+2)2﹣2 B、y=(x﹣4)2+2 C、y=(x﹣1)2﹣1 D、y=(x﹣1)2+52. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )A、 B、4 C、﹣ D、﹣
二、填空题
-
3. 请写出一个函数表达式,使其图象的对称轴为 轴:.4. 二次函数 的图像过点 ,且与y轴交于点B,点M在该抛物线的对称轴上,若 是以 为直角边的直角三角形,则点M的坐标为.5. 下列关于二次函数 ( 为常数)的结论,①该函数的图象与函数 的图象形状相同;②该函数的图象一定经过点 ;③当 时,y随x的增大而减小;④该函数的图象的顶点在函数 的图像上,其中所有正确的结论序号是.6. 加工爆米花时,爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下,可食用率 与加工时间 (单位: )满足函数表达式 ,则最佳加工时间为 .
三、解答题
-
7. 如图在平面直角坐标系中,一次函数 的图像经过点 、 交反比例函数 的图像于点 ,点 在反比例函数的图象上,横坐标为 , 轴交直线 于点 , 是 轴上任意一点,连接 、 .
 (1)、求一次函数和反比例函数的表达式;(2)、求 面积的最大值.8. 某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
(1)、求一次函数和反比例函数的表达式;(2)、求 面积的最大值.8. 某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:销售单价x(元/千克)
55
60
65
70
销售量y(千克)
70
60
50
40
(1)、求y(千克)与x(元/千克)之间的函数表达式;(2)、为保证某天获得600元的销售利润,则该天的销售单价应定为多少?(3)、当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?9. 若二次函数 的图像与x轴有两个交点 ,且经过点 过点A的直线l与x轴交于点 与该函数的图象交于点B(异于点A).满足 是等腰直角三角形,记 的面积为 的面积为 ,且 . (1)、抛物线的开口方向(填“上”或“下”);(2)、求直线 相应的函数表达式;(3)、求该二次函数的表达式.10. 在平面直角坐标系中,O为坐标原点,直线 交二次函数 的图像于点A, ,点 在该二次函数的图象上,设过点 (其中 )且平行于 轴的直线交直线 于点M,交直线 于点N,以线段 、 为邻边作矩形 .
(1)、抛物线的开口方向(填“上”或“下”);(2)、求直线 相应的函数表达式;(3)、求该二次函数的表达式.10. 在平面直角坐标系中,O为坐标原点,直线 交二次函数 的图像于点A, ,点 在该二次函数的图象上,设过点 (其中 )且平行于 轴的直线交直线 于点M,交直线 于点N,以线段 、 为邻边作矩形 . (1)、若点A的横坐标为8.
(1)、若点A的横坐标为8.①用含m的代数式表示M的坐标;
②点 能否落在该二次函数的图象上?若能,求出m的值;若不能,请说明理由;
(2)、当 时,若点 恰好落在该二次函数的图象上,请直接写出此时满足条件的所有直线 的函数表达式.11. 小明和小丽先后从A地出发同一直道去B地, 设小丽出发第 时, 小丽、小明离B地的距离分别为 、 , 与x之间的数表达式 , 与x之间的函数表达式是 .(1)、小丽出发时,小明离A地的距离为 .(2)、小丽发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?12. 如图,在平面直角坐标系中,函数 的图像交 轴于点 、 ,交 轴于点 ,它的对称轴交 轴于点 .过点 作 轴交抛物线于点 ,连接 并延长交 轴于点 ,交抛物线于点 .直线 交 于点 ,交抛物线于点 ,连接 、 .

备用图
(1)、点 的坐标为:;(2)、当 是直角三角形时,求 的值;(3)、 与 有怎样的位置关系?请说明理由.13. 如图①,直线l经过点(4,0)且平行于y轴,二次函数y=ax2﹣2ax+c(a、c是常数,a<0)的图象经过点M(﹣1,1),交直线l于点N,图象的顶点为D,它的对称轴与x轴交于点C,直线DM、DN分别与x轴相交于A、B两点. (1)、当a=﹣1时,求点N的坐标及 的值;(2)、随着a的变化, 的值是否发生变化?请说明理由;(3)、如图②,E是x轴上位于点B右侧的点,BC=2BE,DE交抛物线于点F.若FB=FE,求此时的二次函数表达式.
(1)、当a=﹣1时,求点N的坐标及 的值;(2)、随着a的变化, 的值是否发生变化?请说明理由;(3)、如图②,E是x轴上位于点B右侧的点,BC=2BE,DE交抛物线于点F.若FB=FE,求此时的二次函数表达式.
14. 如图,二次函数 、 的图像分别为 、 , 交 轴于点 ,点 在 上,且位于 轴右侧,直线 与 在 轴左侧的交点为 . (1)、若 点的坐标为 , 的顶点坐标为 ,求 的值;(2)、设直线 与 轴所夹的角为 .
(1)、若 点的坐标为 , 的顶点坐标为 ,求 的值;(2)、设直线 与 轴所夹的角为 .①当 ,且 为 的顶点时,求 的值;
②若 ,试说明:当 、 、 各自取不同的值时, 的值不变;
(3)、若 ,试判断点 是否为 的顶点?请说明理由.15. 二次函数 的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C,顶点为E.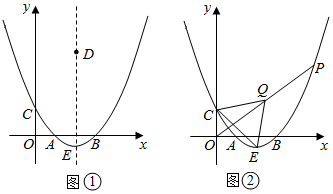 (1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.16. 已知抛物线y=ax2+bx+c经过A(2,0),B(3n﹣4,y1),C(5n+6,y2)三点,对称轴是直线x=1.关于x的方程ax2+bx+c=x有两个相等的实数根.(1)、求抛物线的解析式;(2)、若n<﹣5,试比较y1与y2的大小;(3)、若B,C两点在直线x=1的两侧,且y1>y2 , 求n的取值范围.17. 有一块矩形地块 , 米, 米,为美观,拟种植不同的花卉,如图所示,将矩形 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形 和 中种植甲种花卉;在等腰梯形 和 中种植乙种花卉;在矩形 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米 、60 元/米 、40元/米 ,设三种花卉的种植总成本为y元.
(1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.16. 已知抛物线y=ax2+bx+c经过A(2,0),B(3n﹣4,y1),C(5n+6,y2)三点,对称轴是直线x=1.关于x的方程ax2+bx+c=x有两个相等的实数根.(1)、求抛物线的解析式;(2)、若n<﹣5,试比较y1与y2的大小;(3)、若B,C两点在直线x=1的两侧,且y1>y2 , 求n的取值范围.17. 有一块矩形地块 , 米, 米,为美观,拟种植不同的花卉,如图所示,将矩形 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形 和 中种植甲种花卉;在等腰梯形 和 中种植乙种花卉;在矩形 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米 、60 元/米 、40元/米 ,设三种花卉的种植总成本为y元.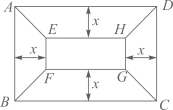 (1)、当 时,求种植总成本y;(2)、求种植总成本y与x的函数表达式,并写出自变量x的取值范围;(3)、若甲、乙两种花卉的种植面积之差不超过120米 ,求三种花卉的最低种植总成本.18. 如图,二次函数 的图像与 轴正半轴交于点A,平行于x轴的直线l与该抛物线交于B、C两点(点B位于点C左侧),与抛物线对称轴交于点 .
(1)、当 时,求种植总成本y;(2)、求种植总成本y与x的函数表达式,并写出自变量x的取值范围;(3)、若甲、乙两种花卉的种植面积之差不超过120米 ,求三种花卉的最低种植总成本.18. 如图,二次函数 的图像与 轴正半轴交于点A,平行于x轴的直线l与该抛物线交于B、C两点(点B位于点C左侧),与抛物线对称轴交于点 . (1)、求b的值;(2)、设P、Q是x轴上的点(点P位于点Q左侧),四边形 为平行四边形.过点P、Q分别作x轴的垂线,与抛物线交于点 、 .若 ,求 、 的值.19. 在平面直角坐标系 中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线 的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线 与 是“共根抛物线”,其顶点为P.
(1)、求b的值;(2)、设P、Q是x轴上的点(点P位于点Q左侧),四边形 为平行四边形.过点P、Q分别作x轴的垂线,与抛物线交于点 、 .若 ,求 、 的值.19. 在平面直角坐标系 中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线 的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线 与 是“共根抛物线”,其顶点为P.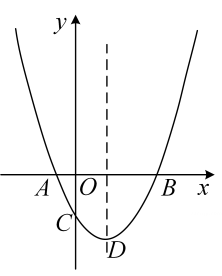
 (1)、若抛物线 经过点 ,求 对应的函数表达式;(2)、当 的值最大时,求点P的坐标;(3)、设点Q是抛物线 上的一个动点,且位于其对称轴的右侧.若 与 相似,求其“共根抛物线” 的顶点P的坐标.20. 如图①,二次函数 的图象与直线l交于 、 两点.点P是x轴上的一个动点,过点P作x轴的垂线交直线l于点M,交该二次函数的图象于点N,设点P的横坐标为m.
(1)、若抛物线 经过点 ,求 对应的函数表达式;(2)、当 的值最大时,求点P的坐标;(3)、设点Q是抛物线 上的一个动点,且位于其对称轴的右侧.若 与 相似,求其“共根抛物线” 的顶点P的坐标.20. 如图①,二次函数 的图象与直线l交于 、 两点.点P是x轴上的一个动点,过点P作x轴的垂线交直线l于点M,交该二次函数的图象于点N,设点P的横坐标为m.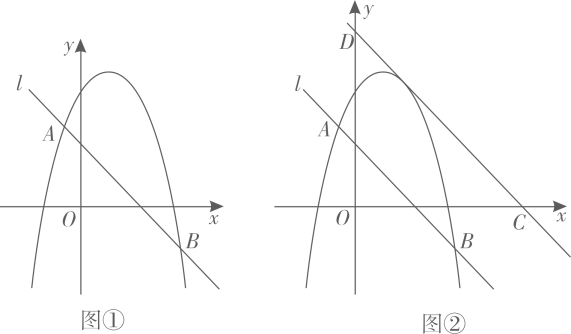 (1)、 , ;(2)、若点N在点M的上方,且 ,求m的值;(3)、将直线 向上平移4个单位长度,分别与x轴、y轴交于点C、D(如图②).
(1)、 , ;(2)、若点N在点M的上方,且 ,求m的值;(3)、将直线 向上平移4个单位长度,分别与x轴、y轴交于点C、D(如图②).①记 的面积为 , 的面积为 ,是否存在m,使得点N在直线 的上方,且满足 ?若存在,求出m及相应的 、 的值;若不存在,请说明理由.
②当 时,将线段 绕点M顺时针旋转 得到线段 ,连接 、 、 ,若 ,直接写出直线 与该二次函数图象交点的横坐标.
21. 如图,二次函数 的图像与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点 ,且顶点为D,连接 、 、 、 .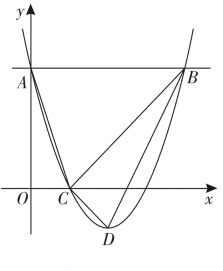
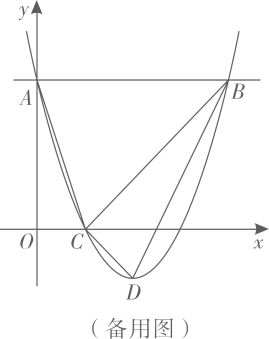 (1)、填空: ;(2)、点P是抛物线上一点,点P的横坐标大于1,直线 交直线 于点Q.若 ,求点P的坐标;(3)、点E在直线 上,点E关于直线 对称的点为F,点F关于直线 对称的点为G,连接 .当点F在x轴上时,直接写出 的长.
(1)、填空: ;(2)、点P是抛物线上一点,点P的横坐标大于1,直线 交直线 于点Q.若 ,求点P的坐标;(3)、点E在直线 上,点E关于直线 对称的点为F,点F关于直线 对称的点为G,连接 .当点F在x轴上时,直接写出 的长.