广东省阳江市阳东区2019-2020学年八年级上学期数学期中试卷
试卷更新日期：2020-09-09 类型：期中考试
一、单选题
-
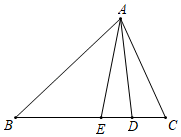
1. 已知三角形两边长分别为3和8，则该三角形第三边的长可能是（ ）A、5 B、10 C、11 D、122. 如图，AE是△ABC的角平分线，AD是△AEC的角平分线，若∠BAC＝80°，则∠EAD＝（ ）
A、30° B、45° C、20° D、60°3. 在△ABC中，∠A=20°，∠B=60°，则△ABC的形状是（ ）A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形4. 一个多边形从一个顶点最多能引出三条对角线，这个多边形是（ ）A、三角形 B、四边形 C、五边形 D、六边形5. 如图，△ABC≌△DCB，点A、B的对应顶点分别为点D、C，如果AB＝7cm，BC＝12cm，AC＝9cm，那么BD的长是（ ）．
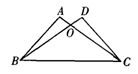A、7cm B、9cm C、12cm D、无法确定6. 如图， 平分 ，E为AB上点若 ， 则下列结论错误的是（ ）
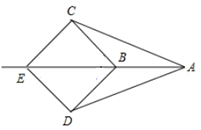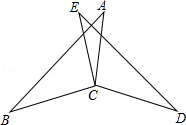
A、 B、 C、 平分 D、图中共有两对全等三角形7. 如图所示，AC和BD相交于O，AO＝DO，AB⊥AC，CD⊥BD，那么AB与CD的关系是（ ）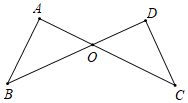
A、一定相等 B、可能相等也可能不相等 C、一定不相等 D、增加条件后，它们相等8. 如图所示，点D在△ABC外部，点E在BC边上，DE交AC于F，若∠1＝∠2，∠D＝∠C，AE＝AB，则（ ）
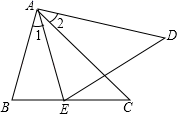A、△ABC≌△AFE B、△AFE≌△ADC C、△AFE≌△DFC D、△ABC≌△AED9. 如图，Rt△ABC，∠C=90°，AD平分∠CAB，DE⊥AB于E，则下列结论中错误的是（ ）
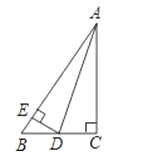A、BD+ED=BC B、DE平分∠ADB C、AD平分∠EDC D、ED+AC＞AD10. 到△ABC的三条边距离相等的点是△ABC的（ ）．A、三条中线的交点 B、三条边的垂直平分线的交点 C、三条高的交点 D、三条角平分线的交点二、填空题
-
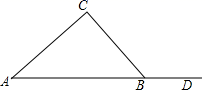
11. 在Rt△ABC中，已知∠C=90°，∠B=46°，则∠A的度数为 ．12. 如图，在△ABC中，∠A＝40°，点D为AB的延长线上一点，且∠CBD＝120°，则∠C＝ ．
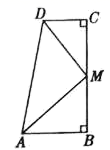
13. 在圆、正六边形、正方形、等边三角形中，对称轴的条数最少的图形是 ．14. 若三角形的外角中有一个是锐角，则这个三角形是三角形．15. 一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为 ．16. 如图所示，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是AE=1，CF=2，则EF长为 ．
17. 如图， 是直角三角形， ， ， 分别是 的高和中线， ， ， ， 则 的面积为 ．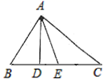
三、解答题
-
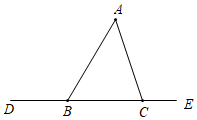
18. 已知△ABC中，AB＝6，BC＝4，求AC的取值范围．19. 如图，∠ABD＝125°，∠A＝50°，求∠ACE的度数．
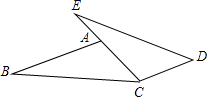
20. 如图，已知四边形ABCD和直线l，求作四边形ABCD以直线l为对称轴的对称图形A1B1C1D1 ．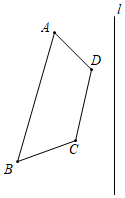
21. 已知：如图，点E，A，C在同一条直线上，AB∥CD，AB=CE，AC=CD．求证：BC=ED．
22. 如图，已知 于 ， 于 ， ， ．证明： ．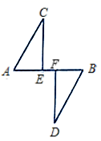
23. 如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E；求证：BC=DC．
