广东省深圳市罗湖区2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-09 类型：期中考试

进入出卷网下载

一、单选题

1. 在实数 $\sqrt{2}$ ， $\frac{2}{17}$ ， $- 0. \overset{•}{7} \overset{•}{3}$ ，3.14， $\sqrt[3]{5}$ ，0，10.12112111211112…，π， $\sqrt{{(- 4)}^{2}}$ 中，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列哪个点在函数 $y = \frac{1}{2} x + 1$ 的图象上（）

A、 $(2, 1)$ B、 $(- 2, 1)$ C、 $(- 2, 0)$ D、 $(2, 0)$

查看试题解析
3. 如图，两个较大正方形的面积分别为225，289，则字母A所代表的正方形的面积为（）

A、4 B、8 C、16 D、64

查看试题解析
4. 已知点P（m+3，2m+4）在x轴上，那么点P的坐标为（）

A、（﹣1，0） B、（1，0） C、（﹣2，0） D、（2，0）

查看试题解析
5. △ABC的三条边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是（）

A、a²+b²=c² B、a=5，b=12，c=13 C、∠A=∠B+∠C D、∠A：∠B：∠C=3：4：5

查看试题解析
6. 下列各式的计算中，正确的是（）

A、 $\sqrt{(- 3) \times (- 9)} = \sqrt{- 3} \times \sqrt{- 9}$ B、 $\sqrt{6} \div \sqrt{3} = \sqrt{3}$ C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $\sqrt{2} - 3 \sqrt{2} = - 2 \sqrt{2}$

查看试题解析
7. 在函数y＝ $\frac{\sqrt{x}}{x - 1}$ 中，自变量x的取值范围是（）

A、x≥1 B、x≤1且x≠0 C、x≥0且x≠1 D、x≠0且x≠1

查看试题解析
8.
如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm至D点，则橡皮筋被拉长了（　　）

A、2cm B、3cm C、4cm D、5cm

查看试题解析
9. 化简二次根式 $a \sqrt[]{- \frac{a + 2}{a^{2}}}$ 的结果是（）

A、 $\sqrt{- a - 2}$ B、－ $\sqrt{- a - 2}$ C、 $\sqrt{a - 2}$ D、－ $\sqrt{a - 2}$

查看试题解析
10. 如图，在正方形ABCD纸片上有一点P，PA＝1，PD＝2，PC＝3，现将△PCD剪下，并将它拼到如图所示位置（C与A重合，P与G重合，D与D重合），则∠APD的度数为（）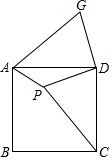

A、150° B、135° C、120° D、108°

查看试题解析
11. 如图1，点G为BC边的中点，点H在AF上，动点P以每秒2cm的速度沿图1的边运动，运动路径为G→C→D→E→F→H，相应的△ABP的面积y（cm²）关于运动时间t（s）的函数图象如图2，若AB＝6cm，则下列结论正确的个数有（）
①图1中BC长4cm；

②图1中DE的长是6cm；

③图2中点M表示4秒时的y值为24cm²；

④图2中的点N表示12秒时y值为15cm² ．

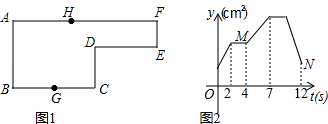A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

12. -27 的立方根为, $\sqrt{16}$ 的平方根为, $- \frac{\sqrt{5}}{5}$ 的倒数为.

查看试题解析
13. 已知函数y＝（a+1）x+a²﹣1，当a时，它是一次函数；当a时，它是正比例函数．

查看试题解析
14. 如图，△ABC的边BC在数轴上，AB⊥BC，且BC＝3，AB＝1，以C为圆心，AC长为半径画圆分别交数轴于点A′、点A″，那么数轴上点A′、点A″所表示的数分别是、.

查看试题解析
15. 如图，在平面直角坐标系中，点A₁ ， A₂ ， A₃…都在x轴上，点B₁ ， B₂ ， B₃…都在直线y=x上，OA₁=1，且△B₁A₁A₂ ， △B₂A₂A₃ ， △B₃A₃A₄ ， …△B_n A_n A_n+1…分别是以A₁ ， A₂ ， A₃ ， …A_n…为直角顶点的等腰直角三角形，则△B₁₀A₁₀A₁₁的面积是.

查看试题解析

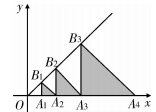
三、解答题

16. 计算：|1﹣ $\sqrt{3}$ |+（2019﹣50 $\sqrt{2}$ ）⁰﹣（ $\frac{1}{2}$ ）^﹣2

查看试题解析
17. $\frac{\sqrt{8} + \sqrt{18}}{\sqrt{2}} + (2 \sqrt{6} + \sqrt{3}) (2 \sqrt{6} - \sqrt{3}) - {(3 \sqrt{3} - \sqrt{2})}^{2}$

查看试题解析
18. 如图，在平面直角坐标系中，正方形ABCD和正方形EFGC面积分别为64和16．

(1)、请写出点A，E，F的坐标；

(2)、求S_△BDF ．

查看试题解析
19. 观察：∵ $\sqrt{4}$ ＜ $\sqrt{7}$ ＜ $\sqrt{9}$ ，即2＜ $\sqrt{7}$ ＜3，∴ $\sqrt{7}$ 的整数部分为2，小数部分为 $\sqrt{7}$ ﹣2，请你观察上述式子规律后解决下面问题．

(1)、规定用符号[m]表示实数m的整数部分，例如：[ $\frac{4}{5}$ ]＝0，[π]＝3，填空：[ $\sqrt{10}$ +2]＝；[5﹣ $\sqrt{13}$ ]＝．

(2)、如果5+ $\sqrt{13}$ 的小数部分为a，5﹣ $\sqrt{13}$ 的小数部分为b，求a²﹣b²的值．

查看试题解析
20. 如图，在长方形ABCD中，AB=8，AD=10，点E为BC上一点，将△ABE沿AE折叠，使点B落在长方形内点F处，且DF=6．

(1)、试说明：△ADF是直角三角形；

(2)、求BE的长．

查看试题解析
21. 如图：

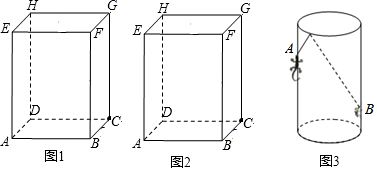(1)、如图1，长方体的长为4cm，宽为3cm，高为12cm．求该长方体中能放入木棒的最大长度；

(2)、如图2，长方体的长为4cm，宽为3cm，高为12cm．现有一只蚂蚁从点A处沿长方体的表面爬到点G处，求它爬行的最短路程．

(3)、若将题中的长方体换成透明圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为10cm，在容器内壁离底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处．求蚂蚁吃到饭粒需要爬行的最短路程是多少？

查看试题解析
22. 看图解答问题：

如图（1），是两个全等的直角三角形（直角边分别为a，b，斜边为c）

(1)、用这样的两个三角形构造成如图（2）的图形，利用这个图形，证明：a²+b²＝c²；

(2)、用这样的两个三角形构造图3的图形，你能利用这个图形证明出题（1）的结论吗？如果能，请写出证明过程；

(3)、当a＝3，b＝4时，将其中一个直角三角形放入平面直角坐标系中，使直角顶点与原点重合，两直角边a，b分别与x轴、y轴重合（如图4中Rt△AOB的位置）．点C为线段OA上一点，将△ABC沿着直线BC翻折，点A恰好落在x轴上的D处．
①请写出C、D两点的坐标；

②若△CMD为等腰三角形，点M在x轴上，请直接写出符合条件的所有点M的坐标．

查看试题解析