广东省深圳市龙华区联考2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-09 类型:期中考试
一、单选题
-
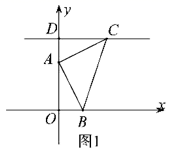
1. 16的平方根是( )A、4 B、 C、 D、2. 李晨想做一个直角三角形的木架,以下四组木棒中,哪一组的三条能够刚好做成?( )A、2,3,4 B、3,4,5 C、4,5,6 D、1,1,23. 下列坐标点在第四象限内的是( )A、(1,2) B、(﹣1,﹣2) C、(﹣1,2) D、(1,﹣2)4. 下列各数中是无理数的是( )A、1 B、 C、0 D、5. 如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )
 A、90° B、60° C、30° D、45°6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,一棵大树在离地面6米高的 处断裂,树顶 落在离树底部 的8米处,则大树断裂之前的高度为( )
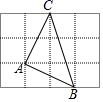
A、90° B、60° C、30° D、45°6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,一棵大树在离地面6米高的 处断裂,树顶 落在离树底部 的8米处,则大树断裂之前的高度为( ) A、10米 B、16米 C、15米 D、14米8. 估计 的值在两个整数( )A、3与4之间 B、5与6之间 C、6与7之间 D、28与30之间9. 已知坐标平面内,线段 轴,点 , ,则B点坐标为( )A、 B、 C、 或 D、 或10. 下列说法正确的是( )A、无限小数都是无理数 B、 没有立方根 C、正数的两个平方根互为相反数 D、 没有平方根11. 在一次“寻宝”人找到了如图所示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都是 ,则“宝藏”点的坐标是( )
A、10米 B、16米 C、15米 D、14米8. 估计 的值在两个整数( )A、3与4之间 B、5与6之间 C、6与7之间 D、28与30之间9. 已知坐标平面内,线段 轴,点 , ,则B点坐标为( )A、 B、 C、 或 D、 或10. 下列说法正确的是( )A、无限小数都是无理数 B、 没有立方根 C、正数的两个平方根互为相反数 D、 没有平方根11. 在一次“寻宝”人找到了如图所示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都是 ,则“宝藏”点的坐标是( ) A、(1,0) B、(5,4) C、(1,0)或(5,4) D、(0,1)或(4,5)12. 如图,在 中, , , ,点 在 上, , 交 于点 ,交 于点 ,则 的长是( )
A、(1,0) B、(5,4) C、(1,0)或(5,4) D、(0,1)或(4,5)12. 如图,在 中, , , ,点 在 上, , 交 于点 ,交 于点 ,则 的长是( ) A、1.5 B、1.8 C、2 D、2.5
A、1.5 B、1.8 C、2 D、2.5二、填空题
-
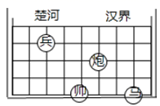
13. 点 关于 轴的对称点的坐标为 .14. 如图,若在象棋盘上建立平面直角坐标系,使“帅”的坐标为 ,“马”的坐标为 ,则“兵”的坐标为 .
 15. 如图四边形OBCD是正方形,在数轴上点A表示的实数.
15. 如图四边形OBCD是正方形,在数轴上点A表示的实数. 16. 观察下列各式: = -1, = , =2- …请利用你发现的规律计算:
16. 观察下列各式: = -1, = , =2- …请利用你发现的规律计算:( + + +…+ )×( + )= .
三、解答题
-
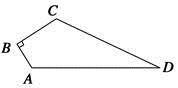
17. 计算:(1)、(2)、18.(1)、(2)、19. 已知:如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
 20. 如图,在平面直角坐标系中有一个 ,顶点 , , .
20. 如图,在平面直角坐标系中有一个 ,顶点 , , .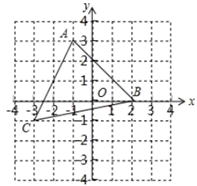 (1)、画出 关于 轴的对称图形 (不写画法);(2)、若P是 轴上的动点,则 的最小值为 .(3)、若网格上的每个小正方形的边长为1,则 的面积是 .21. 如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米.
(1)、画出 关于 轴的对称图形 (不写画法);(2)、若P是 轴上的动点,则 的最小值为 .(3)、若网格上的每个小正方形的边长为1,则 的面积是 .21. 如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米. (1)、这个云梯的底端B离墙多远?(2)、如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?
(1)、这个云梯的底端B离墙多远?(2)、如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?