广东省汕头市潮南区2019-2020学年八年级上学期数学期中试卷
试卷更新日期：2020-09-09 类型：期中考试
一、单选题
-
1. 下列图形中不是轴对称图形的是（ ）A、
B、
C、
D、
2. 根据下列条件不能唯一画出△ABC的是（ ）A、AB=5，BC=6，AC=7 B、AB=5，BC=6，∠B=45° C、AB= 5，AC=4，∠C=90° D、AB=5，AC=4，∠C=45°3. 在△ABC中，2(∠A + ∠B)=3∠C，则∠C的补角等于（ ）
A、36° B、72° C、108° D、144°4. 若正多边形的一个外角是 ，则该正多边形的内角和为（ ）A、 B、 C、 D、5. 如图，已知∠1＝∠2，添加下列某条件，未必能判定△ABC≌△BAD的是（ ）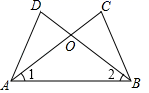
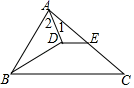
A、∠DAB＝∠CBA B、∠C＝∠D C、BD＝AC D、AD＝BC6. 已知 是 的三边长，化简 的值是（ ）A、 B、 C、 D、7. 如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝( )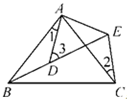
A、60° B、55° C、50° D、无法计算8. 如图，已知∠ACB=60°，PC=12，点M，N在边CB上，PM=PN．若MN=3，则CM的长为（ ）
A、3 B、3.5 C、4 D、4.59. 如图所示．△ABC中，∠B=∠C，D在BC上，∠BAD=50°，AE=AD，则∠EDC的度数为（ ）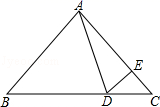
A、15° B、25° C、30° D、50°10. 如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，DH⊥BC于H，交BE于G，下列结论：①BD=CD；②AD+CF=BD；③CE= BF；④AE=BG．其中正确的是（ ）
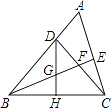A、①② B、①③ C、①②③ D、①②③④二、填空题
-
11. 若△ABC中，∠ACB是钝角，AD是BC边上的高，若AD＝2，BD＝3．CD＝1，则△ABC的面积等于 ．12. 在△ABC中，∠A＝30°，当∠B＝度时，AC＝BC．13. 如图，若AB=AC，BD=CD，∠A=80°，∠BDC=120°，则∠B=°.
14. 若点M（a+b，1）与点N（2，a﹣b）关于y轴对称，则ab的值为 ．15. 已知∠AOB＝60°，OC是∠AOB的平分线，点D为OC上一点，过D作直线DE⊥OA，垂足为点E，且直线DE交OB于点F，如图所示，若DE＝1，则DF＝ ．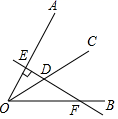
16. 两块完全一样的含30°角的直角三角板，将它们重叠在一起并绕其较长直角边的中点M转动，使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C，如图所示，已知AC=6，则这两块直角三角板顶点A、A′之间的距离等于 ．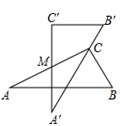
三、解答题
-
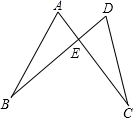
17. 如图，已知线段AC，BD相交于点E，AE＝DE，BE＝CE，求证：△ABE≌△DCE．
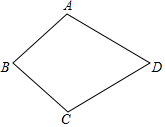
18. 已知在△ABC中，EC平分∠ACB，∠1＝∠2，若∠ACE＝23°，求∠EDC的度数．
19. 如图，四边形ABCD中，AD＝CD，∠A＝∠C．求证：AB＝BC．
20. 如图，∠MON及ON上一点A．求作：点P，使得PA⊥ON，且点P到∠MON两边的距离相等.
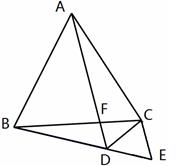
21. 已知：如图，点A、D、C、B在同一条直线上，AD=BC，AE=BF，CE=DF，求证：AE∥BF.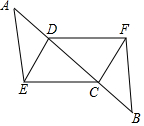
22. 如图：在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于点E，点F在AC上，且BD=DF，
(1)、求证：CF=EB；(2)、请你判断AE、AF与BE之间的数量关系，并说明理由.
