广东省茂名市高州市2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-09 类型：期中考试

进入出卷网下载

一、单选题

1. 已知一个直角三角形的两边长分别为3和4，则第三边长是（）

A、5 B、25 C、 $\sqrt{7}$ D、5或 $\sqrt{7}$

查看试题解析
2. 在实数3.14159，1.010010001，4.21，π， $- \frac{\sqrt{3}}{2}$ ， $\frac{22}{7}$ 中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 如图是在方格纸上画出的小旗图案，若用(2，1)表示A点，(2，5)表示B点，那么C点的位置可表示为（）

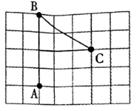A、(3，5) B、(4，3) C、(3，4) D、(5，3)

查看试题解析
4. 下列函数中，正比例函数是（）

A、 $y = \frac{2}{5 x}$ B、 $y = \frac{2}{5} x - 1$ C、 $y = \frac{4}{5} x^{2}$ D、 $y = - \frac{2}{5} x$

查看试题解析
5. 小明准备测量一段河水的深度，他把一根竹竿直插到离岸边6米远的水底，竹竿高出水面2米，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（）

A、7m B、8m C、9m D、10m

查看试题解析
6. 下列等式不成立的是（）

A、6 $\sqrt{2} \times \sqrt{3}$ ＝6 $\sqrt{6}$ B、 $\sqrt{8} \div \sqrt{2} = 4$ C、 $\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$ D、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$

查看试题解析
7. 在平面直角坐标系中，点 $P(-2,3)$ 关于x轴对称的点的坐标为（）

A、 $(2,-3)$ B、 $(-2,-3)$ C、 $(3,-2)$ D、 $(2,3)$

查看试题解析
8. 如图，正方形ABCD的边长为4，点A的坐标为（﹣1，1），AB平行于x轴，则点C的坐标为（）

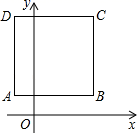A、（2，4） B、（2，5） C、（3，4） D、（3，5）

查看试题解析
9. 有两棵树，一棵高6米，另一棵高3米，两树相距4米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了（）米．

A、3 B、4 C、5 D、6

查看试题解析
10. 在如图所示的数轴上，点B与点C关于点A对称，A，B两点对应的实数分别是 $\sqrt{3}$ 和﹣1，则点C所对应的实数是（）

A、1+ $\sqrt{3}$ B、2+ $\sqrt{3}$ C、2 $\sqrt{3}$ ﹣1 D、2 $\sqrt{3}$ +1

查看试题解析

二、填空题

11. 点M(3，4)与x轴的距离是个单位长度，与原点的距离是个单位长度。

查看试题解析
12. 25的算术平方根是， $\sqrt{9}$ 的平方根是。

查看试题解析
13. 13．若3，4，a和5，b，13是两组勾股数，则a＋b的值是．

查看试题解析
14. 如果点P(m+3，m+1)在x轴上，则点P的坐标为。

查看试题解析
15. 在Rt△ABC中，∠C＝90°，AB＝10，BC＝8，则AC＝．

查看试题解析
16. 若y= $\sqrt{x - 3}$ + $\sqrt{3 - x}$ +2，则x^y= ．

查看试题解析

三、解答题

17. 计算： ${(\sqrt{2} - π)}^{0} + {(\frac{1}{2})}^{- 2} - \sqrt{9} + \sqrt[3]{- 27}$ .

查看试题解析
18. 如图，强大的台风使得一根旗杆在离地面3m处折断倒下，旗杆顶部落在离旗杆底部4m处，旗杆折断之前有多高？

查看试题解析
19. 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题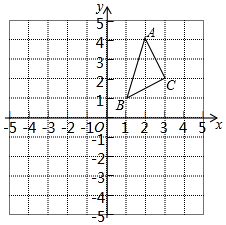

(1)、画出将△ABC向左平移4个单位长度后得到的图形△A₁B₁C₁ ，并写出点C₁的坐标；

(2)、画出将△ABC关于原点O对称的图形△A₂B₂C₂ ，并写出点C₂的坐标．

查看试题解析
20. 计算：

(1)、 $3 \sqrt{20} - \sqrt{45} - \sqrt{\frac{1}{5}}$

(2)、 $(\sqrt{5} - \sqrt{2}) (\sqrt{5} + \sqrt{2}) + {(\sqrt{3} - 1)}^{2}$

查看试题解析
21. 如图，圆柱形容器高为16cm，底面周长为24cm，在杯内壁离杯底的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处，则蚂蚁A处到达B处的最短距离为多少?

查看试题解析
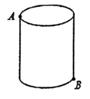22. 已知y是关于x的函数： $y = (m - 3) x^{| m | - 2} + n - 2$ .

(1)、当 $m$ ， $n$ 为何值时，是一次函数；

(2)、当 $m$ ， $n$ 为何值时，是正比例函数.

查看试题解析
23. 如图，在四边形ABCD中，AB＝BC＝2，CD＝3，AD＝1，且∠ABC＝90°，连接AC．

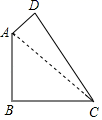(1)、求AC的长度．

(2)、求证△ACD是直角三角形．

(3)、求四边形ABCD的面积？

查看试题解析
24. 观察下列一组式子的变形过程，然后回答问题：
例1： $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)}$ $= \frac{\sqrt{2} - 1}{（ \sqrt{2} ）^{2} - 1} = \frac{\sqrt{2} - 1}{1} = \sqrt{2} - 1$

例2： $\frac{1}{\sqrt{3} + \sqrt{2}}$ = $\sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}}$ = $\sqrt{4} - \sqrt{3}$ ， $\frac{1}{\sqrt{5} + \sqrt{4}} = \sqrt{5} - \sqrt{4}$

利用以上结论解答以下问题：（不必证明）

(1)、 $\frac{1}{\sqrt{6} + \sqrt{5}} =$ ； $\frac{1}{\sqrt{100} + \sqrt{99}} =$ ；
$\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ 。

(2)、利用上面结论，求下列式子的值。
$\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ... + \frac{1}{\sqrt{100} + \sqrt{99}}$

查看试题解析
25. 如图，在平面直角坐标系中，A（a，0），B（b，0），C（﹣1，2），且|a+2|+（b﹣4）²＝0

(1)、求a，b的值；

(2)、在y轴上是否存在一点M，使△COM的面积＝ $\frac{1}{2}$ △ABC的面积，求出点M的坐标．

查看试题解析