广东省江门市恩平市2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-09 类型:期中考试
一、单选题
-
1. 下列图案是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. n边形的内角和为 ,则这个多边形的边数是( )A、4 B、5 C、6 D、83. 点(3,2)关于x轴的对称点为( )A、(3,﹣2) B、(﹣3,2) C、(﹣3,﹣2) D、(2,﹣3)4. 等腰三角形的边长为2和3,那么它的周长为( )A、8 B、7 C、8或7 D、以上都不对5. 如图, 是 的平分线 上一点, 于 , 于 ,下列结论中错误的是( )
A、1个 B、2个 C、3个 D、4个2. n边形的内角和为 ,则这个多边形的边数是( )A、4 B、5 C、6 D、83. 点(3,2)关于x轴的对称点为( )A、(3,﹣2) B、(﹣3,2) C、(﹣3,﹣2) D、(2,﹣3)4. 等腰三角形的边长为2和3,那么它的周长为( )A、8 B、7 C、8或7 D、以上都不对5. 如图, 是 的平分线 上一点, 于 , 于 ,下列结论中错误的是( )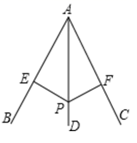 A、 B、 C、 D、6. 如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )
A、 B、 C、 D、6. 如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为( )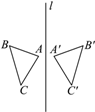 A、48° B、54° C、74° D、78°7. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A、48° B、54° C、74° D、78°7. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( ) A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF8. 如图,△ABC中,AB=AC,D为BC的中点,以下结论:(1)△ABD≌△ACD ;(2)AD⊥BC;(3)∠B=∠C ;(4)AD是△ABC的角平分线。其中正确的有( )。
A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF8. 如图,△ABC中,AB=AC,D为BC的中点,以下结论:(1)△ABD≌△ACD ;(2)AD⊥BC;(3)∠B=∠C ;(4)AD是△ABC的角平分线。其中正确的有( )。 A、1个 B、2个 C、3个 D、4个9. 将一副直角三角板,按如图所示叠放在一起,则图中∠
A、1个 B、2个 C、3个 D、4个9. 将一副直角三角板,按如图所示叠放在一起,则图中∠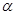 的度数是( )
的度数是( ) 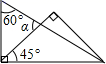 A、45o B、60o C、75o D、90o
A、45o B、60o C、75o D、90o二、填空题
-
10. 如图所示,在 中, , ,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于 的长为半径画弧,两弧交于点P , 连接AP并延长交BC于点D , 则下列说法中正确的有 .
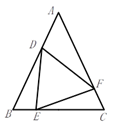
①AD是 的平分线;② ;③点D在AB的中垂线上;④
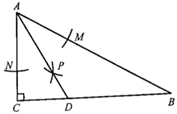 11.
11.如图,为了防止门板变形,小明在门板上钉了一根加固木条,从数学的角度看,这样做的理由是利用了三角形的。
 12. 如图,在△ABC中,∠C=40°,CA=CB,则△ABC的外角∠ABD=°.
12. 如图,在△ABC中,∠C=40°,CA=CB,则△ABC的外角∠ABD=°.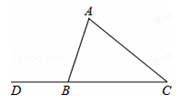 13. 三角形的三边长分别为5,x,8,则x的取值范围是 .14. 一个多边形的内角和为1080°,则这个多边形是边形.15. 如图,将等边三角形 剪去一个角后,则 的大小为.
13. 三角形的三边长分别为5,x,8,则x的取值范围是 .14. 一个多边形的内角和为1080°,则这个多边形是边形.15. 如图,将等边三角形 剪去一个角后,则 的大小为.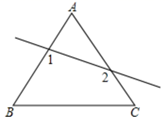 16. 如图,一种机械工件,经测量得∠A=20°,∠C=27°,∠D=45°.那么不需工具测量,可知∠ABC=°.
16. 如图,一种机械工件,经测量得∠A=20°,∠C=27°,∠D=45°.那么不需工具测量,可知∠ABC=°.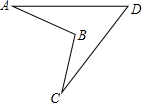
三、解答题
-
17. 一个多边形的内角和是外角和的3倍,它是几边形?18. 如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.
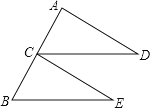 19. 如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.
19. 如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等. (1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)、连结AD,若∠B=37°,求∠CAD的度数.20. 如图, 处在 处的南偏西 方向, 处在 处的南偏东 方向, 处在 处的北偏东 方向,求从 处看 、 两处的视角 是多少度.
(1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)、连结AD,若∠B=37°,求∠CAD的度数.20. 如图, 处在 处的南偏西 方向, 处在 处的南偏东 方向, 处在 处的北偏东 方向,求从 处看 、 两处的视角 是多少度. 21. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
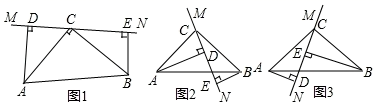
21. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.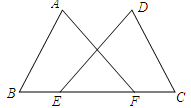 22. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形, , , 在同一条直线上,连结 .
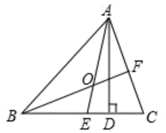
22. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形, , , 在同一条直线上,连结 .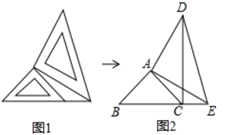 (1)、请写出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)、证明: .23. 如图所示,在 中, 是高, 、 是角平分线,它们相交于点 , , ,求 、 的度数.
(1)、请写出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)、证明: .23. 如图所示,在 中, 是高, 、 是角平分线,它们相交于点 , , ,求 、 的度数.