广东省广州市实验教育集团2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-09 类型:期中考试
一、单选题
-
1. 下列四个图形中,不是轴对称图形的是( )A、
 B、
B、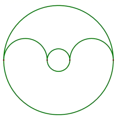 C、
C、 D、
D、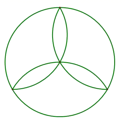 2. 若有两条线段长分别为3cm和4cm,则下列长度的线段能与其组成三角形的是( )A、1cm B、5cm C、7cm D、9cm3. 如图,在△ABC中,BC边上的高为( )
2. 若有两条线段长分别为3cm和4cm,则下列长度的线段能与其组成三角形的是( )A、1cm B、5cm C、7cm D、9cm3. 如图,在△ABC中,BC边上的高为( )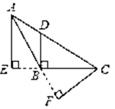 A、BD B、CF C、AE D、BF4. 如图, , , .则 的度数为( )
A、BD B、CF C、AE D、BF4. 如图, , , .则 的度数为( )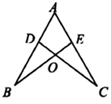 A、 B、 C、 D、5. 如图,在 Rt△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交BC于点D,连接AD,则△ACD的周长是( )
A、 B、 C、 D、5. 如图,在 Rt△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交BC于点D,连接AD,则△ACD的周长是( ) A、7 B、8 C、9 D、106. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
A、7 B、8 C、9 D、106. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )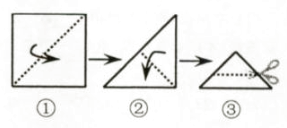 A、
A、 B、
B、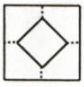 C、
C、 D、
D、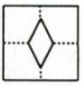 7. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
7. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )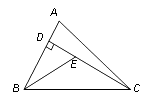 A、5 B、7 C、10 D、38. 下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )A、①②③④ B、①②④ C、①③ D、②③④9. 如图,在 中, 平分 交AB于点M,过点 作 交 于点 ,且 平分 ,若 ,则BC的长为( )
A、5 B、7 C、10 D、38. 下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )A、①②③④ B、①②④ C、①③ D、②③④9. 如图,在 中, 平分 交AB于点M,过点 作 交 于点 ,且 平分 ,若 ,则BC的长为( )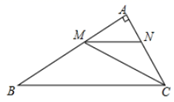 A、4 B、6 C、5 D、810. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )
A、4 B、6 C、5 D、810. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )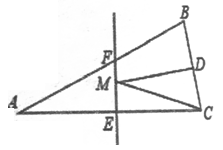 A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12二、填空题
-
11. 已知点 , 关于x轴对称,则 .12. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .13. 如图,在 和 中,已知 , ,要使 ,还需添加一个条件,那么这个条件可以是(填出一个即可).
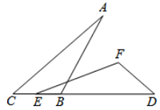 14. 如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=30°,∠AEB=80°,∠CAD的度数为 .
14. 如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=30°,∠AEB=80°,∠CAD的度数为 . 15. 如图,平面直角坐标系中,A(1,0)、B(0,2),BA=BC,∠ABC=90°,则点 C 的坐标为
15. 如图,平面直角坐标系中,A(1,0)、B(0,2),BA=BC,∠ABC=90°,则点 C 的坐标为 16. 在如图所示的方格纸中,每个小方格都是边长为1的正方形,A、B是方格纸中的两个格点(即正方形的顶点).在这张5×5的方格纸中,找出格点C,使△ABC为等腰三角形,则满足条件的格点C有个.
16. 在如图所示的方格纸中,每个小方格都是边长为1的正方形,A、B是方格纸中的两个格点(即正方形的顶点).在这张5×5的方格纸中,找出格点C,使△ABC为等腰三角形,则满足条件的格点C有个.
三、解答题
-
17. 如图,A(0,﹣2),B(2,﹣3),C(4,﹣1);
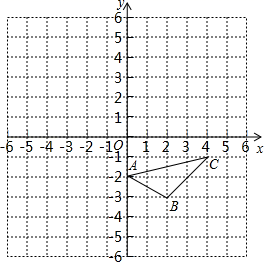 (1)、在图中作出△ABC关于y轴的对称图形△A1B1C1(2)、写出点A1 , B1 , C1的坐标:
(1)、在图中作出△ABC关于y轴的对称图形△A1B1C1(2)、写出点A1 , B1 , C1的坐标:A1( , ),B1( , ),C1( , ).
18. 如图,已知点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AC∥DF。 19. 如图, 处在 的南偏西 方向, 处在 处的南偏东 方向, 处在 处的北偏东 方向,求 的度数.
19. 如图, 处在 的南偏西 方向, 处在 处的南偏东 方向, 处在 处的北偏东 方向,求 的度数. 20. 如图, 中, , , 是 边上的中线, 是 上一点且 ,求 的度数.
20. 如图, 中, , , 是 边上的中线, 是 上一点且 ,求 的度数.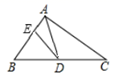 21. 如图,在⊿ 中, ,点 分别在 边上,且 , .
21. 如图,在⊿ 中, ,点 分别在 边上,且 , .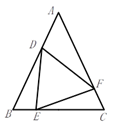 (1)、求证:⊿ 是等腰三角形;
(1)、求证:⊿ 是等腰三角形;
(2)、当 时,求 的度数.22. 如图,已知△ABC是等边三角形,D是边AC的中点,连接BD,EC⊥BC于点C,CE=BD.求证:△ADE是等边三角形.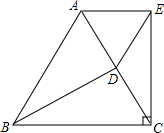 23. 如图,在 中, 平分 .
23. 如图,在 中, 平分 . (1)、尺规作图(不写作法,保留作图痕迹),作 的垂真平分线 ,与 相交于点 ,与 相交于点 ;(2)、在(1)条件下,连接 , , 和 有何数量关系?并证明你的结论.24. 如图,在平面直角坐标系中, 、 坐标为 、 , 为线段 上的一点.
(1)、尺规作图(不写作法,保留作图痕迹),作 的垂真平分线 ,与 相交于点 ,与 相交于点 ;(2)、在(1)条件下,连接 , , 和 有何数量关系?并证明你的结论.24. 如图,在平面直角坐标系中, 、 坐标为 、 , 为线段 上的一点.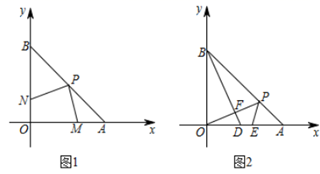 (1)、如图1,若 为 的中点,点 、 分别是 、 边上的动点,且保持 ,则在点 、 运动的过程中,探究线段 、 之间的位置关系与数量关系,并说明理由.(2)、如图2,若 为线段 上异于 、 的任意一点,过 点作 ,交 、 分别于 、 两点, 为 上一点,且 ,试判断线段 与 的数量关系,并说明理由.25. 如图,等边 中, ,点 在 上, ,点 从点 出发,以每秒1个单位长度的速度沿 方向向点 运动, 关于 的轴对称图形为 .
(1)、如图1,若 为 的中点,点 、 分别是 、 边上的动点,且保持 ,则在点 、 运动的过程中,探究线段 、 之间的位置关系与数量关系,并说明理由.(2)、如图2,若 为线段 上异于 、 的任意一点,过 点作 ,交 、 分别于 、 两点, 为 上一点,且 ,试判断线段 与 的数量关系,并说明理由.25. 如图,等边 中, ,点 在 上, ,点 从点 出发,以每秒1个单位长度的速度沿 方向向点 运动, 关于 的轴对称图形为 .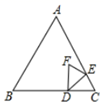 (1)、当t为何值时,点 在线段 上;(2)、当 时,求 与 的数量关系;(3)、当点 、 、 三点共线时,求证:点 为线段 的中点.
(1)、当t为何值时,点 在线段 上;(2)、当 时,求 与 的数量关系;(3)、当点 、 、 三点共线时,求证:点 为线段 的中点.