安徽省淮南市2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-09 类型:期中考试
一、单选题
-
1. 下列标志中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是( )A、3,3,6 B、1,5,5 C、1,2,3 D、8,3,43. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC的长是( )
2. 下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是( )A、3,3,6 B、1,5,5 C、1,2,3 D、8,3,43. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC的长是( ) A、4 B、5 C、6 D、74. 已知一个等腰三角形的两边长a、b满足方程组 则此等腰三角形的周长为( )A、5 B、4 C、3 D、5或45. 一个多边形的每个内角均为108º,则这个多边形是( )A、七边形 B、六边形 C、五边形 D、四边形6.
A、4 B、5 C、6 D、74. 已知一个等腰三角形的两边长a、b满足方程组 则此等腰三角形的周长为( )A、5 B、4 C、3 D、5或45. 一个多边形的每个内角均为108º,则这个多边形是( )A、七边形 B、六边形 C、五边形 D、四边形6.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
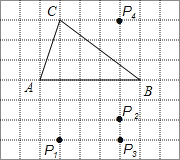 A、1个 B、2个 C、3个 D、4个7. 如图,已知AB∥CD , OA、OC分别平分∠BAC和∠ACD , OE⊥AC于点E , 且OE=2,则AB、CD之间的距离为( )
A、1个 B、2个 C、3个 D、4个7. 如图,已知AB∥CD , OA、OC分别平分∠BAC和∠ACD , OE⊥AC于点E , 且OE=2,则AB、CD之间的距离为( ) A、2 B、4 C、6 D、88. 如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=4cm2 , 则阴影部分面积S=( )cm2 .
A、2 B、4 C、6 D、88. 如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=4cm2 , 则阴影部分面积S=( )cm2 . A、1 B、2 C、3 D、49. 如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A=( ).
A、1 B、2 C、3 D、49. 如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A=( ). A、60° B、80° C、70° D、50°10. 如图所示,在矩形纸片 中, , 为 边上两点,且 ; , 为 边上两点,且 .沿虚线 折叠,使点 落在点 上,点 落在点 上;然后再沿虚线 折叠,使 落在点 上,点 落在点 上.叠完后,剪一个直径在 上的半圆,再展开,则展开后的图形为( )
A、60° B、80° C、70° D、50°10. 如图所示,在矩形纸片 中, , 为 边上两点,且 ; , 为 边上两点,且 .沿虚线 折叠,使点 落在点 上,点 落在点 上;然后再沿虚线 折叠,使 落在点 上,点 落在点 上.叠完后,剪一个直径在 上的半圆,再展开,则展开后的图形为( ) A、
A、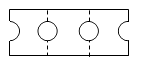 B、
B、 C、
C、 D、
D、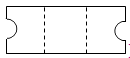
二、填空题
-
11. 点(3,2)关于x轴的对称点为12. 若一个多边形的内角和是它的外角和的4倍,则这个多边形的边数是.13. 若等腰三角形的一个内角为50°,则它的顶角为 .14. 如图,∠B=46°,△ABC的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为 .
 15. 如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则 : : 等于 .
15. 如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则 : : 等于 . 16. 若直角三角形的一锐角为30°,而斜边与较短边之和为24.那么斜边的长为.17. 已知P(m﹣4,3m﹣7)关于y轴的对称点在第一象限,则m的整数解为.18. 如图,在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是.
16. 若直角三角形的一锐角为30°,而斜边与较短边之和为24.那么斜边的长为.17. 已知P(m﹣4,3m﹣7)关于y轴的对称点在第一象限,则m的整数解为.18. 如图,在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是. 19. 如图,点P是∠AOB内任意一点,OP=5,M , N分别是射线OA和OB上的动点,若△PMN周长的最小值为5,则∠AOB的度数为 .
19. 如图,点P是∠AOB内任意一点,OP=5,M , N分别是射线OA和OB上的动点,若△PMN周长的最小值为5,则∠AOB的度数为 . 20. 如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是(填序号)
20. 如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是(填序号)
三、解答题
-
21. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(
 ,5),(
,5),(  ,3).
,3).  (1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、请作出△ABC关于y轴对称的△A′B′C′;(3)、写出点B′的坐标.22. 如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:BD=EC。
(1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、请作出△ABC关于y轴对称的△A′B′C′;(3)、写出点B′的坐标.22. 如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:BD=EC。 23. 如图,点D是△ABC中BC边上一点,E是AD上一点EB=EC , ∠BAE=∠CAE,求证:∠ABE=∠ACE.
23. 如图,点D是△ABC中BC边上一点,E是AD上一点EB=EC , ∠BAE=∠CAE,求证:∠ABE=∠ACE. 24. 如图①,△ABC中,AB=AC , ∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
24. 如图①,△ABC中,AB=AC , ∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.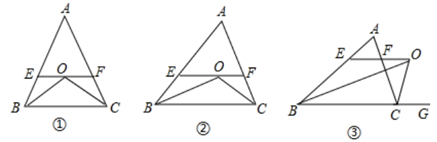 (1)、图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.(2)、如图②,若AB≠AC , 其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)、如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O , 过O点作OE∥BC交AB于E , 交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
(1)、图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.(2)、如图②,若AB≠AC , 其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)、如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O , 过O点作OE∥BC交AB于E , 交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.