安徽省合肥市庐江县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-09 类型:期中考试
一、单选题
-
1. 下列交通标志中,属于轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段能组成三角形的是( )A、3,3,6 B、5,6,11 C、6,6,6 D、9,9,193. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、
2. 下列长度的三条线段能组成三角形的是( )A、3,3,6 B、5,6,11 C、6,6,6 D、9,9,193. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、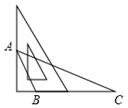 B、
B、 C、
C、 D、
D、 4. 如图,△ABC≌△DEF,则∠E的度数为( )
4. 如图,△ABC≌△DEF,则∠E的度数为( )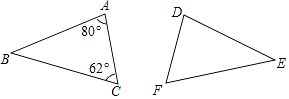 A、80° B、40° C、62° D、38°5. 一个多边形的内角和比外角和的 倍多 ,则它的边数是( )A、八 B、九 C、十 D、十一6. 周长为40cm 的三角形纸片ABC (如图甲),AB= AC,将纸片按图中方式折叠,使点A与点B重合,折痕为DE (如图乙).若 的周长为25cm,则BC的长( ).
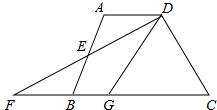
A、80° B、40° C、62° D、38°5. 一个多边形的内角和比外角和的 倍多 ,则它的边数是( )A、八 B、九 C、十 D、十一6. 周长为40cm 的三角形纸片ABC (如图甲),AB= AC,将纸片按图中方式折叠,使点A与点B重合,折痕为DE (如图乙).若 的周长为25cm,则BC的长( ). A、10cm B、12cm C、15cm D、16cm7. 如图,AB⊥CD,CE⊥AF,BF⊥ED.若AB=CD,CE=8,BF=6,AD=10,则EF的长为( ).
A、10cm B、12cm C、15cm D、16cm7. 如图,AB⊥CD,CE⊥AF,BF⊥ED.若AB=CD,CE=8,BF=6,AD=10,则EF的长为( ).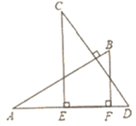 A、4 B、 C、3 D、8. 如图, 中, BP平分∠ABC, AP⊥BP于P,连接PC,若 的面积为3.5cm2 , 的面积为4.5cm2 , 则 的面积为( ).
A、4 B、 C、3 D、8. 如图, 中, BP平分∠ABC, AP⊥BP于P,连接PC,若 的面积为3.5cm2 , 的面积为4.5cm2 , 则 的面积为( ).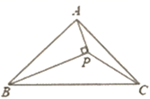 A、0.25cm2 B、0.5 cm2 C、1cm2 D、1.5cm29. 如图,在 中, AB=6,BC=7,AC=4,直线m是 中BC边的垂直平分线,点P是直线m上的一动点.则 周长的最小值为( ).
A、0.25cm2 B、0.5 cm2 C、1cm2 D、1.5cm29. 如图,在 中, AB=6,BC=7,AC=4,直线m是 中BC边的垂直平分线,点P是直线m上的一动点.则 周长的最小值为( ).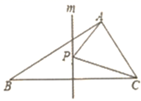 A、10 B、11 C、11.5 D、1310. 如图,AD是 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF,BE=7.5,CF=6,则EF=( ).
A、10 B、11 C、11.5 D、1310. 如图,AD是 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF,BE=7.5,CF=6,则EF=( ). A、2.5 B、2 C、1.5 D、1
A、2.5 B、2 C、1.5 D、1二、填空题
-
11. 已知 ,若 的周长为32, AB=8, BC=12,则FD的长为.12. 如图,一艘轮船在A处看见巡逻艇M在其北偏东62°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上,则∠AMB 度.
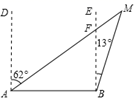 13. 如图,在 中,∠C=90°, AC=8cm,若BD是角平分线,AD=3CD,则点D到AB的距离为.
13. 如图,在 中,∠C=90°, AC=8cm,若BD是角平分线,AD=3CD,则点D到AB的距离为.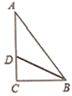 14. 在 中,AH是BC边上的高,若CH- BH= AB, ,则∠BAC= 。
14. 在 中,AH是BC边上的高,若CH- BH= AB, ,则∠BAC= 。三、解答题
-
15. 如图,已知 ,∠C=125°,∠A=45°,求∠E的度数,
 16. 小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD, BE,当他将一个等腰直角三角板ABC如图垂直放入时,直角顶点C正好在水平线DE上,锐角顶点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。
16. 小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD, BE,当他将一个等腰直角三角板ABC如图垂直放入时,直角顶点C正好在水平线DE上,锐角顶点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。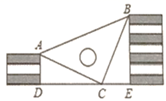 17. 在平面直角坐标系中,△ABC的三个顶点的坐标为A(3,4),B(1,2),C(5,1).
17. 在平面直角坐标系中,△ABC的三个顶点的坐标为A(3,4),B(1,2),C(5,1).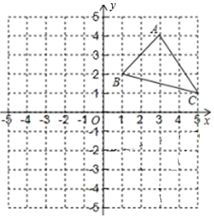 (1)、写出A、B、C关于y轴对称的点A1、B1、C1的坐标: A1、B1、C1;(2)、若 各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A'、B'、C',并依次连接这三个点,判断所得△A′B′C′与原 有怎样的位置关系.18. 如图,给出四个等式:①AB= DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.请你从这四个等式中选出两个作为条件,推出 是等腰三角形. (要求写出所有符合要求的条件,并给出其中一种条件下的证明过程).
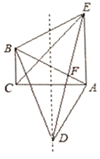
(1)、写出A、B、C关于y轴对称的点A1、B1、C1的坐标: A1、B1、C1;(2)、若 各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A'、B'、C',并依次连接这三个点,判断所得△A′B′C′与原 有怎样的位置关系.18. 如图,给出四个等式:①AB= DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.请你从这四个等式中选出两个作为条件,推出 是等腰三角形. (要求写出所有符合要求的条件,并给出其中一种条件下的证明过程).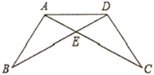 19. 如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.
19. 如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.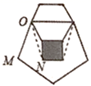 20. 如图,△ABC中,AB=AC,点P、Q、R分别在AB,BC,AC上,且PB=QC,QB=RC.
20. 如图,△ABC中,AB=AC,点P、Q、R分别在AB,BC,AC上,且PB=QC,QB=RC.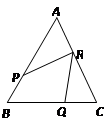
求证:点Q在PR的垂直平分线上.
21. 如图,已知 =30°, 点A1 , A2 , A3 , ……射线ON上,点B1 , B2 , B3..在射线OM上, ,均为等边三角形,若OA1=1.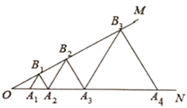 (1)、A1A2=;(2)、求A3A4的长:(3)、根据你发现的规律直接写出A2019A2020的边长.
(1)、A1A2=;(2)、求A3A4的长:(3)、根据你发现的规律直接写出A2019A2020的边长.