安徽省合肥市包河区2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-09 类型：期中考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点（-1， $a^{2} + 1$ ）一定在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 若函数 $y = (k - 4) x + 5$ 是一次函数，则k应满足的条件为（）

A、 $k > 4$ B、 $k < 4$ C、 $k = 4$ D、 $k \neq 4$

查看试题解析
3. 函数 $y = \frac{1}{\sqrt{x + 3}}$ 的自变量x的取值范围是（）

A、 $x > - 3$ B、 $x \geq - 3$ C、 $x \neq - 3$ D、 $x \leq - 3$

查看试题解析
4. 若点 $A (- 1, a)$ ， $B (- 4, b)$ 在一次函数 $y = - 5 x - 3$ 图象上，则a与b的大小关系是（）

A、 $a < b$ B、 $a > b$ C、 $a = b$ D、无法确定

查看试题解析
5. 关于函数 $y = - 3 x + 1$ ，下列结论正确的是（）

A、图象必经过点 $(- 3, 1)$ B、图象经过第一、二、三象限 C、当 $x > \frac{1}{3}$ 时， $y < 0$ D、y随x的增大而增大

查看试题解析
6. 在平面直角坐标系中，过点 $(2, - 1)$ 的直线l经过一二、四象限，若点 $(m, - 2)$ ， $(0, n)$ 都在直线l上，则下列判断正确的是（）

A、 $m < 0$ B、 $m > 2$ C、 $n < - 1$ D、 $n = 0$

查看试题解析
7. 在平面直角坐标系中，点 $P (x ， y)$ 在第一象限内，且 $x + y = 8$ ，点A的坐标为 $(6 ， 0)$ ．设 $△ O P A$ 的面积为S ． S与x之间的函数关系式是（）

A、 $S = - x + 8 (0 < x < 8)$ B、 $S = - 3 x + 24 (0 < x < 8)$ C、 $S = - 3 x + 12 (0 < x < 4)$ D、 $S = - \frac{1}{3} x + 8 (0 < x < 8)$

查看试题解析
8. 如图，直线 $y = k x + b$ 与 $y = m x + n$ 分别交x轴于点 $A (- 0.5 ， 0)$ ， $B (2 ， 0)$ ，则不等式 $(k x + b) (m x + n) < 0$ 的解集为（）

A、 $x > 2$ B、 $0 < x < 2$ C、 $- 0.5 < x < 2$ D、 $x < - 0.5$ 或 $x > 2$

查看试题解析
9. 广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售，在销售了40千克之后，余下的打七五折全部售完．销售金额y（元）与售出西瓜的千克数x（千克）之间的关系如图所示．下列结论正确的是（）

A、降价后西瓜的单价为2元/千克 B、广宇一共进了50千克西瓜 C、售完西瓜后广宇获得的总利润为44元 D、降价前的单价比降价后的单价多0.6元

查看试题解析
10. 如图，在 $△ A B C$ 中，E是BC上一点， $B C = 3 B E$ ，点F是AC的中点，若 $S_{△ A B C} = a$ ，则 $S_{△ A D F} - S_{△ B D E} =$ （）

A、 $\frac{1}{2} a$ B、 $\frac{1}{3} a$ C、 $\frac{1}{6} a$ D、 $\frac{1}{12} a$

查看试题解析

二、填空题

11. 点Q在第四象限内，并且到x轴的距离为3，到y轴的距离为5，则点Q的坐标为．

查看试题解析
12. 已知y+2与x-1成正比例关系，且当x=3时，y=2，则y=3时，x= ．

查看试题解析
13. 已知BD是 $△ A B C$ 的中线， $A B = 7$ ， $B C = 3$ ，且 $△ A B D$ 的周长为15，则 $△ B C D$ 的周长为．

查看试题解析
14. 已知n为整数，若一个三角形的三边长分别是 $4 n + 31$ ， $n - 13$ ，6n ，则所有满足条件的n值的和为．

查看试题解析
15. 对于点 $P (a ， b)$ ，点 $Q (c ， d)$ ，如果 $a - b = c - d$ ，那么点P与点Q就叫作等差点，例如：点 $P (1 ， 2)$ ，点 $Q (- 1 ， 0)$ ，因为 $1 - 2 = - 1 - 0 = - 1$ ，则点P与点Q就是等差点，如图在矩形（长方形）GHMN中，点 $H (3 ， 5)$ ，某点 $N (- 3 ， - 5)$ ， $M N ⊥ y$ 轴， $H M ⊥ x$ 轴，点P是直线 $y = x + b$ 上的任意一点（点P不在矩形的边上），若矩形GHMN的边上存在两个点与点P是等差点，则 $b$ 的取值范围为．

查看试题解析
16. 已知当 $- 2 \leq x \leq 3$ 时，函数 $y = | 2 x - m |$ （其中m为常量）的最小值为 $2 m - 54$ ，则m= ．

查看试题解析

三、解答题

17. 在平面直角坐标系中，有 $A (- 2, a + 2)$ ， $B (a - 3, 4)$ ， $C (b - 4, b)$ 三点．

(1)、当 $A B ∥ x$ 轴时，求A、B两点间的距离；

(2)、当 $C D ⊥ x$ 轴于点D ，且 $C D = 3$ 时，求点C的坐标．

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ B = ∠ A C B$ ， $∠ A = 36^{°}$ ，线段CD和CE分别为 $△ A B C$ 的角平分线和高线．求 $∠ A D C$ 、 $∠ D C E$ 的大小．

查看试题解析
19. 已知一次函数 $y = k x + b$ 的图象与直线 $y = - 2 x + 1$ 平行，且经过点 $(- 1, 5)$ ．

(1)、该一次函数的表达式为；

(2)、若点 $N (a, b)$ 在（1）中所求的函数的图象上，且 $a - b = 6$ ，求点N的坐标．

查看试题解析
20. 如图，直线 $l_{1} ： y = 2 x + 4$ 与直线 $l_{2} ： y = a x + \frac{3}{2}$ 相交于点 $A (- 1 ， b)$ ．

(1)、 $a =$ ； $b =$ ．

(2)、经过点 $(m ， 0)$ 且垂直于x轴的直线与直线 $l_{1}$ ， $l_{2}$ 分别交于点M ， N ，若线段MN长为5，求m的值．

查看试题解析
21. 2019年暑假期间，某学校计划租用8辆客车送280名师生参加社会实践活动，现有甲、乙两种客车，它们的载客量和租金如表，设租用甲种客车x辆，租车总费用为w元．

甲种客车

乙种客车

载客量（人/辆）

30

40

租金（元/辆）

270

320

(1)、求出w（元）与x（辆）之间函数关系式，并直接写出自变量x的取值范围；

(2)、选择怎样的租车方案所需的费用最低？最低费用多少元？

查看试题解析
22. 如图，一只蚂蚁在网格（每小格边长为1）上沿着网格线运动．它从格点 $A (1 ， 2)$ 处出发去看望格点B、C、D等处的蚂蚁，规定：向上向右走均为正，向下向左走均为负．如：从A到B记为： $A \to B 〈 + 1 ， + 3 〉$ ，从B到A记为： $B \to A 〈 - 1 ， - 3 〉$ ，其中第一个数表示左右方向，第二个数表示上下方向．

(1)、填空：图中 $A \to C <____，____>$ ， $C \to____<____， \underline{^{} + 3^{}} >$ ；

(2)、若这只蚂蚁从A处去M处的蚂蚁的行走路线依次为 $〈 + 3 ， + 3 〉$ ， $〈 + 2 ， - 1 〉$ ， $〈 - 3 ， - 3 〉$ ， $〈 + 4 ， + 2 〉$ ，则点M的坐标为（，）；

(3)、若图中另有两个格点Р、Q ，且 $P \to A < m + 3 ， n + 2 >$ ， $P \to Q 〈 m + 1 ， n - 2 〉$ ，则从Q到A记为．

查看试题解析
23. 甲、乙两人驾车都从Р地出发，沿一条笔直的公路匀速前往Q地，乙先出发一段时间后甲再出发，甲、乙两人到达Q地后均停止，已知P、Q两地相距200 km，设乙行驶的时间为t（h），甲、乙两人之间的距离为y（km），表示y与t函数关系的部分图象如图所示．请解决以下问题：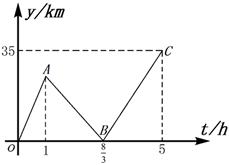

(1)、由图象可知，甲比乙迟出发h．图中线段BC所在直线的函数解析式为；

(2)、设甲的速度为 $v_{1} km / h$ ，求出 $v_{1}$ 的值；

(3)、根据题目信息补全函数图象（不需要写出分析过程，但必须标明关键点的坐标）；并直接写出当甲、乙两人相距32 km时t的值．

查看试题解析

	甲种客车	乙种客车
载客量（人/辆）	30	40
租金（元/辆）	270	320