安徽省滁州市全椒县2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-09 类型：期中考试

进入出卷网下载

一、单选题

1. 在函数 $y = \frac{\sqrt{x}}{x - 1}$ 中，自变量 $x$ 的取值范围是（）

A、 $x > 0$ B、 $x > 1$ C、 $x > 0$ 且 $x \neq 1$ D、 $x ⩾ 0$ 且 $x \neq 1$

查看试题解析
2. 已知点 $A (2 a + 1, b - 2)$ 在第三象限，则点 $B (- a, 3 - b)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 以下列各组线段的长为边，能组成三角形的是（）

A、2、4、7 B、3、5、2 C、7、7、3 D、9、5、3

查看试题解析
4. 2012年“国际攀岩比赛”在重庆举行．小丽从家出发开车前去观看，途中发现忘了带门票，于是打电话让妈妈马上从家里送来，同时小丽也往回开，遇到妈妈后聊了一会儿，接着继续开车前往比赛现场．设小丽从家出发后所用时间为t，小丽与比赛现场的距离为S．下面能反映S与t的函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
5. 若一个三角形的三条边长分别为3，2a-1，6，则整数a的值可能是（）

A、2，3 B、3，4 C、2，3，4 D、3，4，5

查看试题解析
6. 已知点P(﹣1，y₁)、点Q(3，y₂)在一次函数y＝(2m﹣1)x+2的图象上，且y₁＞y₂ ，则m的取值范围是（）

A、m< $\frac{1}{2}$ B、m> $\frac{1}{2}$ C、m≥1 D、m＜1

查看试题解析
7. 如图，在 $Δ A B C$ 中， $A D ⊥ B C$ ， $A E$ 平分 $∠ B A C$ ，若 $∠ B A E = 30 °$ ， $∠ C A D = 20 °$ ，则 $∠ B$ 的度数为（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
8. 已知二元一次方程组 ${\begin{array}{l} x + y = 5 \\ 2 x - y = 1 \end{array}$ 的解是 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，则一次函数 $y = - x + 5$ 与 $y = 2 x - 1$ 的图象的交点坐标为（）

A、 $(2, 3)$ B、 $(3, 2)$ C、 $(- 2, 3)$ D、 $(2, - 3)$

查看试题解析
9. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE 的中点，且△ABC的面积为4cm² ，则△BEF的面积等于（）

A、2cm² B、1cm² C、0.5 cm² D、0.25 cm²

查看试题解析
10. 如图，在平面直角坐标系中，一动点从原点 $O$ 出发，沿着箭头所示方向，每次移动1个单位，依次得到点 $P_{1} (0 ， 1)$ ， $P_{2} (1 ， 1)$ ， $P_{3} (1 ， 0)$ ， $P_{4} (1 ， - 1)$ ， $P_{5} (2 ， - 1)$ ， $P_{6} (2 ， 0)$ ……则点 $P_{2020}$ 的坐标是（）

A、 $(673 ， - 1)$ B、 $(673 ， 1)$ C、 $(336 ， - 1)$ D、 $(336 ， 1)$

查看试题解析

二、填空题

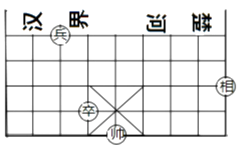
11. 如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是（3，-1）和（-3，1），那么“卒”的坐标为。

查看试题解析
12. 已知：△ABC中，∠A+∠B= $\frac{1}{2}$ ∠C，则∠C =.

查看试题解析
13. 已知直线 $y = - 2 x + 4$ ，则将其向右平移1个单位后与两坐标轴围成的三角形的面积为.

查看试题解析
14. 如图： $A$ 、 $B$ 两地相距 $60 km$ ，甲、乙两人从两地出发相向而行，甲先出发，图中 $l_{1}$ ， $l_{2}$ 表示两人离 $A$ 地的距离 $s (km)$ 与时间 $t (h)$ 的关系，则甲出发后小时，两人恰好相距 $5 km$ .

查看试题解析

三、解答题

15. 已知正比例函数y=kx的图象经过点（3，-6）.

(1)、求这个函数表达式；

(2)、判断点 $A (4, - 2)$ ，点 $B (- 1.5, 3)$ 是否在这个函数的图象上.

查看试题解析
16. 已知点 $P (2 m + 4, m - 1)$ ，试分别根据下列条件，求出 $P$ 点的坐标.

(1)、点 $P$ 在 $y$ 轴上；

(2)、点 $P$ 在过点 $A (2, 3)$ 且与 $x$ 轴平行的直线上.

查看试题解析
17. 已知一次函数 $y = (2 m + 3) x + m - 1$ .

(1)、若该函数的值 $y$ 随自变量 $x$ 的增大而减小，求m的取值范围；

(2)、若该函数图象不经过第二象限，求m的取值范围.

查看试题解析
18. 如图，在平面直角坐标系 $x O y$ 中，点 $A$ 的坐标为(0，4)，线段 $M N$ 的位置如图所示，其中点 $M$ 的坐标为( $- 3$ ， $- 1$ )，点 $N$ 的坐标为(3， $- 2$ ).

(1)、将线段 $M N$ 平移得到线段 $A B$ ，其中点 $M$ 的对应点为 $A$ ，点 $N$ 的对应点为点 $B$ .
①点 $M$ 平移到点 $A$ 的过程可以是：先向平移个单位长度，再向平移个单位长度；

②点 $B$ 的坐标为.

(2)、在(1)的条件下，若点 $C$ 的坐标为(4，0)，连接 $A C 、 B C$ ，画出图形并求 $Δ A B C$ 的面积.

查看试题解析
19. 用一条长为25cm的绳子围成一个等腰三角形．

(1)、如果腰长是底边长的2倍，那么三角形的各边长是多少？

(2)、能围成有一边的长是6 cm的等腰三角形吗？为什么？

查看试题解析
20. 为响应绿色出行号召，越来越多市民选择租用共享单车出行，已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式，如图描述了两种方式应支付金额y（元）与骑行时间x（时）之间的函数关系，根据图象回答下列问题：

(1)、求手机支付金额y（元）与骑行时间x（时）的函数关系式；

(2)、李老师经常骑行共享单车，请根据不同的骑行时间帮他确定选择哪种支付方式比较合算．

查看试题解析
21. 如图，直线 $y = k x + b$ 经过点 $A (5 ， 0)$ ， $B (1 ， 4)$ .

(1)、求直线 $A B$ 的表达式.

(2)、若直线 $y = 2 x - 4$ 与直线 $A B$ 相交于 $C$ ，求点 $C$ 的坐标.

(3)、根据图像，写出关于 $x$ 的不等式 $2 x - 4 > k x + b$ 的解集.

查看试题解析
22. 在 $Δ A B C$ 和 $Δ D E F$ 中， $∠ A = 40 °$ ， $∠ E + ∠ F = 70 °$ ，将 $Δ D E F$ 放置在 $Δ A B C$ 上，使得 $∠ D$ 的两条边 $D E$ 、 $D F$ 分别经过点B、C.

(1)、当将 $Δ D E F$ 如图（1）放置在 $Δ A B C$ 上时，求 $∠ A B D + ∠ A C D$ 的大小；

(2)、当将 $Δ D E F$ 如图（2）放置在 $Δ A B C$ 上时，求 $∠ A B D + ∠ A C D$ 的大小.

查看试题解析

23. 某农产品生产基地收获红薯192吨，准备运给甲、乙两地的承包商进行包销．该基地用大、小两种货车共18辆恰好能一次性运完这批红薯，已知这两种货车的载重量分别为14吨/吨和8吨/辆，运往甲、乙两地的运费如下表：

车型	运费
车型	运往甲地/（元/辆）	运往乙地/（元/辆）
大货车	720	800
小货车	500	650

(1)、求这两种货车各用多少辆；

(2)、如果安排10辆货车前往甲地，其余货车前往乙地，其中前往甲地的大货车为a辆，总运费为w元，求w关于a的函数关系式；

(3)、在（2）的条件下，若甲地的承包商包销的红薯不少于96吨，请你设计出使总运费最低的货车调配方案，并求出最低总运费．

查看试题解析